Machine Learning Park -- 逻辑回归和Softmax
2 Logistic Regression & Softmax
2.1 Logistic Regression
逻辑回归
本文Github仓库已经同步文章与代码https://github.com/Gary-code/Machine-Learning-Park/tree/main/Part1%20Machine%20Learning%20Basics
- 这是解决分类问题而不是回归问题的!
代码文件说明
| 文件名 | 说明 |
|---|---|
| logistic_numpy.ipynb | 逻辑回归实现(使用a9a数据集) |
| softmax_pytorch_version.ipynb | softmax实现 |
模型构建
- 模型假设
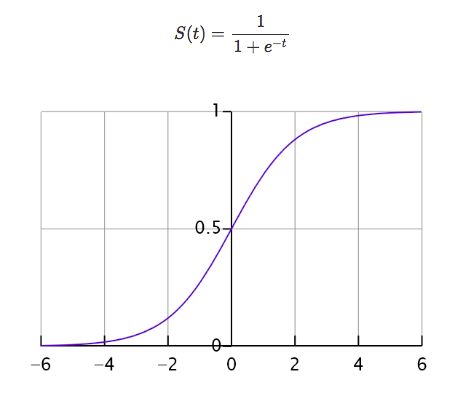
模型的假设是: h θ ( ) = g ( θ ) ℎ_{\theta}() = g( \theta ^) hθ(x)=g(θTX)其中: 代表特征向量 代表逻辑函数(logistic function)是一个常用的逻辑函数为 S 形函数(Sigmoid function),公式为: ( ) = 1 1 + − () = \frac{1}{1+^{−} } g(z)=1+e−z1
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
如果对于给定的,通过已经确定的参数计算得出 h θ ( ) = 0.7 ℎ_{\theta}() = 0.7 hθ(x)=0.7,则表示有 70%的几率为正向类,相应地为负向类的几率为 1-0.7=0.3
- 判断边界
当 h θ ( ) h_{\theta}() hθ(x)>= 0.5时,预测 = 1。
当 h θ ( ) h_{\theta}() hθ(x)< 0.5时,预测 = 0 。
又 = θ = \theta^ z=θTx ,即:
θ \theta^ θTx >= 0 时,预测 = 1
θ \theta^ θTx < 0 时,预测 = 0
- 损失函数
对于线性回归模型,我们定义的损失函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将 h θ ( ) = 1 1 + 1 − θ ℎ_\theta() = \frac{1}{1+^{1−\theta^}} hθ(x)=1+e1−θTX1
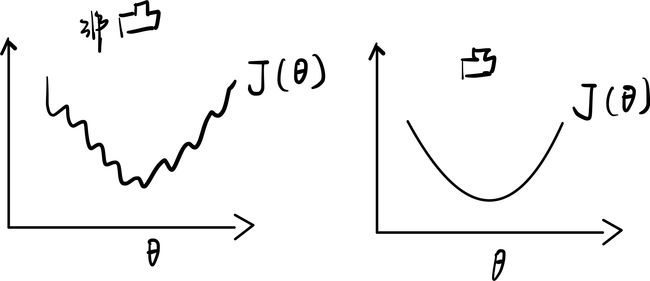
代入到这样定义了的损失函数中时,我们得到的损失函数将是一个非凸函数(non-convexfunction)。
这意味着我们的损失函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
因此我们需要重新定义损失函数:
Cost ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) if y = 1 − log ( 1 − h θ ( x ) ) if y = 0 \operatorname{Cost}\left(h_{\theta}(x), y\right)=\left\{\begin{aligned} -\log \left(h_{\theta}(x)\right) & \text { if } y=1 \\ -\log \left(1-h_{\theta}(x)\right) & \text { if } y=0 \end{aligned}\right. \\ Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x)) if y=1 if y=0
J ( θ ) = 1 2 m ∑ i = 1 m C o s t ( h θ ( x ) , y ) J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}Cost(h_\theta(x), y) J(θ)=2m1i=1∑mCost(hθ(x),y)
import numpy as np
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
return np.sum(first - second) / (len(X))
下面我们对损失函数进行优化
合并上面的式子可以得到:
( h θ ( ) , ) = − × ( h θ ( ) ) − ( 1 − ) × ( 1 − h θ ( ) ) (ℎ_{\theta}(), ) = − × (ℎ_{\theta}()) − (1 − ) × (1 − ℎ_{\theta}()) Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x))
- 梯度下降算法求解
当然除了SGD(梯度下降算法)之外,还有其他的求解方法,但这里不做过多介绍。
2.2 softmax与多分类问题
实际上Softmax回归也是一种分类算法,对比逻辑回归:
- 从二元分类变成多输出分类
模型构建
- 有效编码
这里我们以独热编码(one-hot coding)来举例
y = [ y 1 , y 2 , … , y n ] ⊤ y i = { 1 if i = y 0 otherwise \begin{aligned} &\mathbf{y}=\left[y_{1}, y_{2}, \ldots, y_{n}\right]^{\top} \\ &y_{i}=\left\{\begin{array}{l} 1 \text { if } i=y \\ 0 \text { otherwise } \end{array}\right. \end{aligned} y=[y1,y2,…,yn]⊤yi={1 if i=y0 otherwise
- 无校验比例
最大值最为预测结果:
y ^ = argmax i o i \hat{y}=\underset{i}{\operatorname{argmax}} o_{i} y^=iargmaxoi
-
校验比例(softmax)
-
输出匹配概率
- 非负
- 和为1
y ^ = softmax ( o ) y ^ i = exp ( o i ) ∑ k exp ( o k ) \begin{aligned} &\hat{\mathbf{y}}=\operatorname{softmax}(\mathbf{o}) \\ &\hat{y}_{i}=\frac{\exp \left(o_{i}\right)}{\sum_{k} \exp \left(o_{k}\right)} \end{aligned} y^=softmax(o)y^i=∑kexp(ok)exp(oi)
-
-
损失函数
交叉熵
l ( y , y ^ ) = − ∑ y i log y ^ i = − log y ^ y l(\mathbf{y}, \hat{\mathbf{y}})=-\sum y_{i} \log \hat{y}_{i}=-\log \hat{y}_{y} l(y,y^)=−∑yilogy^i=−logy^y
其梯度就是真实概率和预测概率的区别
∂ o i l ( y , y ^ ) = softmax ( o ) i − y i \partial_{o_{i}} l(\mathbf{y}, \hat{\mathbf{y}})=\operatorname{softmax}(\mathbf{o})_{i}-y_{i} ∂oil(y,y^)=softmax(o)i−yi -
总结
- Softmax回归是一 个多类分类模型
- 使用Softmax操作子得到每个类的预测置信度
- 使用交叉熵来来衡量预测和标号的区别