二叉树遍历——递归链式(C语言实现)
二叉树遍历——递归链式
- 前,中,后序遍历
- 结点个数与叶子个数
- 求第k层的结点个数与树的高度
- 查找值为x的结点与层序遍历
- 销毁二叉树与判断二叉树是否为完全二叉树
前,中,后序遍历
首先我们定义一个结构体,链式储存,那么肯定有一个左孩子和右孩子,自身也要储存值。
typedef char BTDataType;//重命名,方便更改类型
typedef struct BinaryTreeNode
{
BTDataType _data;//自身储存值
struct BinaryTreeNode* _left;//左孩子
struct BinaryTreeNode* _right;//右孩子
}BTNode;
先创建如下的二叉树:
如果二叉树是这种情况,前中后怎么进行遍历呢?
前序遍历:
前序是先访问根节点,再访问左子树,最后访问右子树。(这里要注意,B是A的左子树,C是A的右子树,D是B的左子树,以此类推)
遍历都是从根节点进入的,那么我们第一个访问的肯定是A,然后访问的是结点B,正常来说又要访问结点的C了,但是B结点也有子孙,所以要先访问B的所有子孙才能访问C的子孙。
递归到D结点之后,D就是根节点,两边的空指针就是左右孩子,先进入左孩子,因为是空指针,所以返回到D,再进行右孩子的访问,右孩子也是个空指针,那么也返回到D,D的所有子孙都访问完之后返回B, 然后又要访问B的右边的子孙(也是右树)。
那么顺序就是:A->B->D->NULL->NULL-> E->G->NULL->NULL->NULL->C->F->H->NULL->NULL->I->NULL->NULL->NULL
代码实现:
void BinaryTreePrevOrder(BTNode* root)//最初传入的就是祖先结点A
{
if (root == NULL)//如果遇到空结点就返回
{
printf("NULL ");
return;
}
printf("%c ", root->_data);//打印每个结点中的内容,也等于访问该节点
BinaryTreePrevOrder(root->_left);//进入左
BinaryTreePrevOrder(root->_right);//进入右
}
先写一个函数来测试一下这段函数有没有作用:
void test1()
{
BTNode n1;
BTNode n2;
BTNode n3;
BTNode n4;
BTNode n5;
BTNode n6;
BTNode n7;
BTNode n8;
BTNode n9;
n1._data = 'A';
n1._left = &n2;
n1._right = &n3;
n2._data = 'B';
n2._left = &n4;
n2._right =&n5;
n3._data = 'C';
n3._left = &n6;
n3._right = NULL;
n4._data = 'D';
n4._left = NULL;
n4._right = NULL;
n5._data = 'E';
n5._left = &n7;
n5._right = NULL;
n6._data = 'F';
n6._left = &n8;
n6._right = &n9;
n7._data = 'G';
n7._left = NULL;
n7._right = NULL;
n8._data = 'H';
n8._left = NULL;
n8._right = NULL;
n9._data = 'I';
n9._left = NULL;
n9._right = NULL;
BinaryTreePrevOrder(&n1);
}
int main()
{
test1();
return 0;
}
结果没错。
刚调用这个函数的时候传入的就是祖先节点,不为空就直接打印,然后进入左子树,和右子树,不为空就打印,是空就返回,返回的时候就在原来调用函数的位置,这里最重要的就是顺序。
中序遍历
中序遍历是,先访问左子树,再访问根,最后访问右子树。
知道前序遍历就好办了,那么这里调整一下递归的顺序就好了。
void BinaryTreeInOrder(BTNode* root)//左 根 右
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreeInOrder(root->_left);
printf("%c ", root->_data);
BinaryTreeInOrder(root->_right);
}
递归到D结点的时候再进入D的左子树,发现是空指针返回,然后返回到D的位置在访问D,最后再进行D右子树的访问。
因为一开始并没有进行打印的操作,所以在进入D左边的空指针之前就没有打印途中的A B D,这就是顺序的重要性。

后序遍历
后序遍历是:先访问左,在访问右,在访问根。
这里只要把打印的事情放到最后就好了。
void BinaryTreePostOrder(BTNode* root)//左 右 根
{
if (root == NULL)
{
printf("NULL ");
return;
}
BinaryTreePostOrder(root->_left);//还是先从左开始访问,一直到底
BinaryTreePostOrder(root->_right);
printf("%c ", root->_data);
}

递归到D的位置的时候,先进入D的左树,发现是空指针就返回,返回之后是在D的位置,这里一定不要打印,再进入D的右树,发现是空指针然后返回,这样D的左子树和右子树都访问完成了,最后在进行D的访问。
结点个数与叶子个数
结点个数
计算节点个数可以定义一个全局的静态变量,但是缺点很明显,每次计算完都要重新值置为零,很麻烦。
我们可以利用函数的返回值和递归解决这个问题,核心思路是这样的:
例:
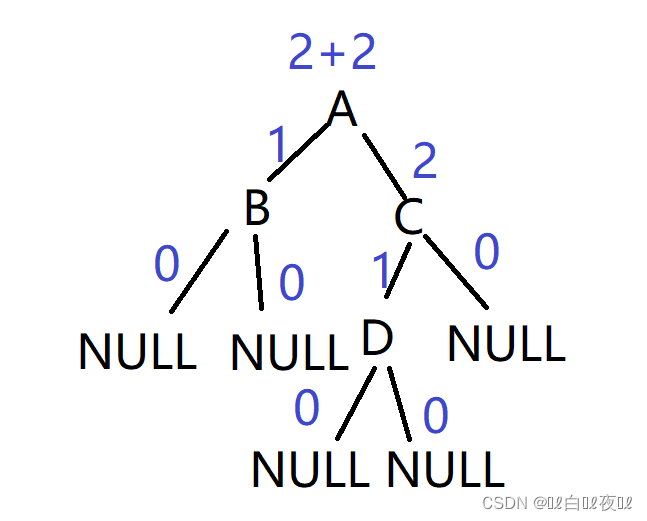
总数应该是祖先结点A+左子树+右子树,左子树里面还有左子树+右子树,右子树里面还有左子树和右子树,就和上面的遍历差不多的逻辑。
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;//如果到了空指针就返回0
}
return BinaryTreeSize(root->_left) +
BinaryTreeSize(root->_right) + 1;//没到空指针就记住这个结点,并且知道找到空指针为止
}
如果找到不是空的结点就用+1记住该节点,遇到空结点就返回0。
这样就不会出现静态全局变量需要重置的问题了。
叶子数量
计算叶子的数量,就要找叶子节点的特点,叶子的特点是孩子节点都是空。
例:

B,D结点的两个孩子都是空,所以是叶子节点,那么代码实现只需要判断一下就可以了。
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL && root->_right == NULL)
{
return 1;//如果孩子都为空就返回1,说明这个结点是叶子节点
}
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);//调用左子树和右子树
}
求第k层的结点个数与树的高度
求k层的节点个数
例:
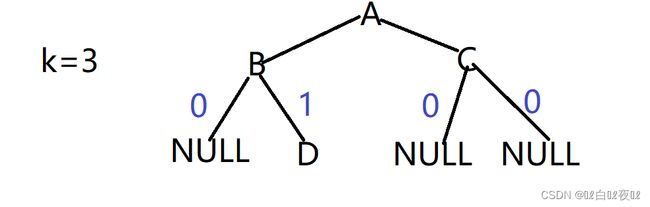
想访问这棵树的第三层,那么这层就等于左子树和右子树的第二层,也就等于k-1,那么直到k等于1,说明这里就是我们要访问的结点。
遇到空就返回0,遇到该层结点就返回1,比如说这棵树,A->B->NULL返回0到B的位置,B->D,到达该层数,返回1到B,然后到A的右子树进行访问。
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);//不能是负数
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
树的高度
例:
思路是,找A的左子树和右子树,最后比一比谁的更长,A的左子树最长的是D,长度为2,右子树最长的是C,长度为1,所以这棵树的高度为2。
int TreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int x = TreeHeight(root->_left);
int y = TreeHeight(root->_right);
return x > y ? x + 1: y + 1;//+1是记录非空结点
}
查找值为x的结点与层序遍历
查找值为x的结点
查找整棵树中的储存的值为x的结点首先需要遍历,然后判断哪个结点是我们要找的结点, 不过返回的时候需要进行判断,不然会出现这种情况:
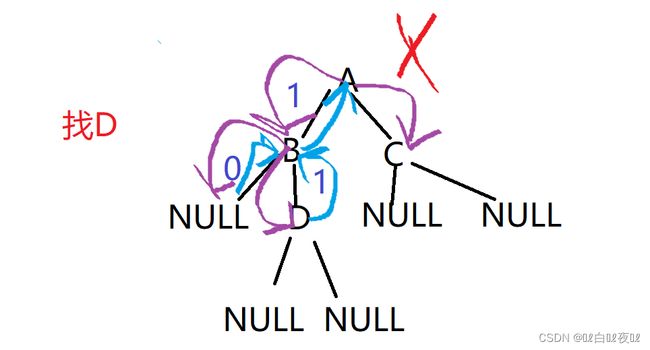
找D的时候,从A的左子树开始找,找不到返回空,找到了返回该节点,但是返回该节点的时候回到的位置是上一个结点的位置,如果没有判断就会去下个树中去找,并且不会将该节点返回到我们需要的地方。
如果加一个判断,顺利的返回就好了。
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
BTNode* x1 =BinaryTreeFind(root->_left, x);//找左子树
if (x1)//判断是否为空,空是找到了,非空是没找到
{
return x1;//找到了就返回找到的结点,位置是上一层的找左子树的函数
}
BTNode* y =BinaryTreeFind(root->_right , x);
if (y)
{
return y;
}
return NULL;
}
这里还可以进行修改值。
层序遍历
层序遍历是一层一层的进行访问:
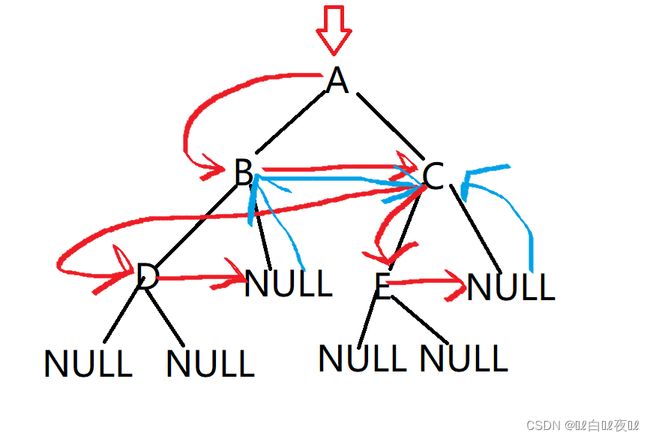
从祖先结点开始,遇到空指针返回。
那么怎么才能把所有的都访问到呢?我们需要借助队列:
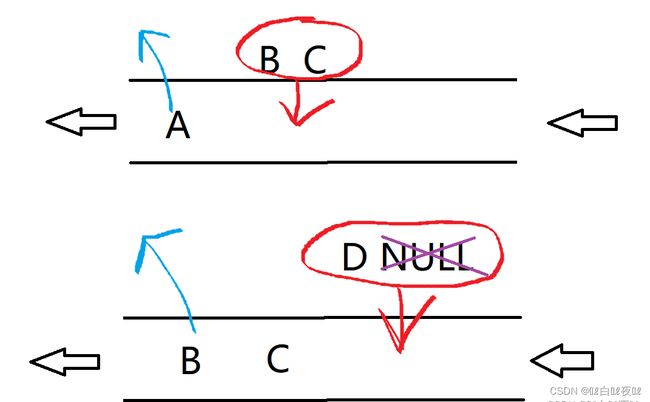
在队中的头结点出队的时候,会将左子树和右子树进行入队操作,如果左子树和右子树中有空指针将不会进行入队操作。
#include #include "queue.h"
void QueueInit(Qu* q)//初始化
{
assert(q);
q->head = q->tail = NULL;
q->siz = 0;
}
void QueueDestroy(Qu* q)//销毁队列
{
assert(q);
QL* cur = q->head;
while (cur)
{
QL* del = cur -> next;
free(cur);
cur = del;
}
q->head = q->tail = NULL;
q->siz = 0;
}
void QueuePush(Qu* q, SD x)//入队
{
assert(q);
QL* w = (QL*)malloc(sizeof(Qu));
if (w == NULL)
{
perror("malloc tail");
exit(-1);
}
else
{
w->data = x;
w->next = NULL;
}
if (q->head == NULL)
{
q->head = q->tail = w;
}
else
{
q->tail->next = w;
q->tail = w;
}
q->siz++;
}
bool QueueEmpty(Qu* q)//判断
{
assert(q);
return q->head == NULL;
}
void QueuePop(Qu* q)//出队
{
assert(q);
assert(!QueueEmpty(q));
if (q->head == NULL)//防止tail成为野指针
{
free(q->head);
q->head = q->tail = NULL;
}
QL* cur = q->head;
q->head = q->head->next;
free(cur);
cur = NULL;
q->siz--;
}
SD QueueFront(Qu* q)//获取队头元素
{
assert(q);
assert(!QueueEmpty(q));
return q->head->data;
}
SD QueueBack(Qu* q)//获取队尾元素
{
assert(q);
assert(!QueueEmpty(q));
return q->tail->data;
}
int QueueSize(Qu* q)//获取队列中有效元素个数
{
assert(q);
return q->siz;
}
#include "queue.h"
void BinaryTreeLevelOrder(BTNode* root)
{
Qu q;
QueueInit(&q);//初始化队列
if (root)//空指针不能入队
{
QueuePush(&q, root);//将结点存入队列中
}
while (!QueueEmpty(&q))//如果为空就不要进行入队和出队的操作了
{
BTNode* Front = QueueFront(&q);//获取队头元素
printf("%c ", Front->_data);//进行打印
QueuePop(&q);//弹出队头元素
if (Front->_left)//判断左子树是不是空指针
QueuePush(&q, Front->_left);
if (Front->_right)//判断右子树是不是空指针
QueuePush(&q, Front->_right);
}
printf("\n");
QueueDestroy(&q);//销毁队列
}
销毁二叉树与判断二叉树是否为完全二叉树
销毁二叉树
销毁树的逻辑也是遍历,然后从底部销毁。
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;//找到底部返回上一层进行释放就可以了
}
BinaryTreeDestory(root->_left);//这里就是先从左子树开始
BinaryTreeDestory(root->_right);
free(root);
}
判断是否为完全二叉树
想判断二叉树是否为一个完全二叉树,就用刚才说的层序遍历:
例:

层序遍历很好查看:
- 当遇到空指针的时候,这一层后面的结点必须都是空指针,
- 下面的一层也必须都是空指针。
向上面的这种肯定不是,至少要吧C的左子树换成空指针,或者是B和C的右子树不是空指针,但是他们右子树的右子树必须是空指针。
这样的话,和层序遍历没啥区别,但是也有,因为我们这里遇到空指针也要入队,不然无法判断下一层是不是空指针。

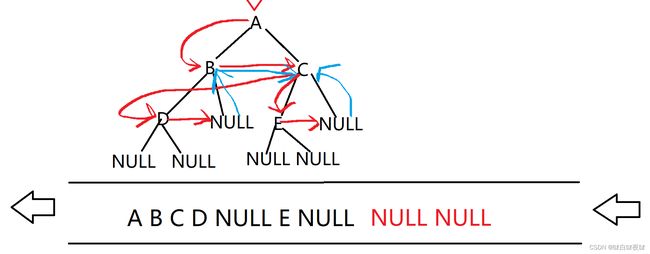
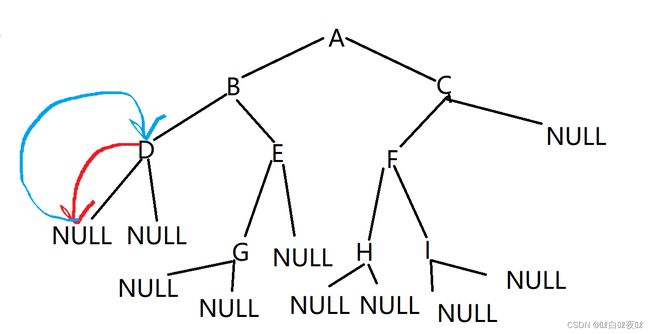
因为A出队B C才会入队,B C出队,他们的子树才能入队,D出队的时候,他的子树也如对了(红色的),这样看来如果E结点是个空结点也不用担心最后一层的NULL不在队中。
当D出队后,下一个访问的就是空指针, 这时候,后面的所有结点都必须是空指针才行,不是就说明是非完全二叉树。
int BinaryTreeComplete(BTNode* root)
{
Qu q;
QueueInit(&q);
QueuePush(&q, root);
while (!QueueEmpty(&q))//还是正常的层序遍历操作
{
BTNode* Front = QueueFront(&q);
if (Front == NULL)
{
break;//这里如果空指针是对头,就跳出进行入队的操作
}
QueuePop(&q);
QueuePush(&q, Front->_left);
QueuePush(&q, Front->_right);
}
while (!QueueEmpty(&q))//判断空指针
{
BTNode* Front = QueueFront(&q);
QueuePop(&q);
if (Front != NULL)//如果队中遇到的不是空指针,那么就不是完全二叉树
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}