电力电子技术->整流电路
整流电路
- 重点总结
- 题型总结
-
- 带漏感的计算
- 选择性查漏补缺
-
- 基本概念
- 单相半波可控整流电路
-
- 基本概念
- 纯电阻负载
-
- α=0°
- α=30°
- U~d~的一般公式
- 阻感负载
-
- 带续流二极管
- 分析方法总结
- 单相桥式全控整流电路
-
- 纯电阻负载
-
- α=0°
-
- 自然换相点的确定(用晶闸管替代)
- 正题
- α=30°
- 阻感负载
- 反电动势负载
-
- 例题
- 三相半波可控整流电路
-
- 纯电阻负载
-
- α=0°
- α=30°
- α=60°
- 阻感负载
-
- α=60°
- 三相桥式全控整流电路
-
- 纯电阻负载
-
- α=0°
-
- 工作特点
- α=30°
- α=60°
- α=90°
- 阻感负载
-
- α<60°
- α≥60°
- α=90°时
- α=60°
- 反电动势阻感负载
- 变压器漏感对整流电路的影响
-
- 单相桥式全控整流电路
-
- 定性分析
- 定量计算换相重叠角
- 三相桥式全控整流电路
- 变压器漏感对整流电路的影响
- 电容滤波的不可控整流电路(#####待补充########)
-
- 电路结构
- 有源逆变(交流侧接电网)
-
- 功率
- 实现有源逆变的条件
- 逆变失败
-
- 产生原因
- 逆变角(触发角α的补角)
- 变压器抗漏对逆变电路换相的影响
- 避免换相失败β~min~
- 谐波
-
- 产生
- 危害
- 整流电路的谐波分析(交流侧电流)
-
- 大电感负载单向桥式
-
- 波形分析
- 电流波形的畸变
- 大电感负载三相整流电路
-
- 波形分析
- 功率因数及增大无功消耗的危害
- 晶闸管整流电路的功率因数
-
- 单相整流电路
- 三相整流电路
- 总结
- 大功率可控整流电路
-
- 带平衡电抗器的双反星形可控整流电路
- 多重化整流电路
- 参考资料
重点总结
晶闸管导通的条件:正向电压,门级触发电流
触发延迟角:晶闸管开始承受正向电压起,到施加触发脉冲为止的电角度。
cos α − cos ( α + γ ) = 2 ω L B I d 2 U 2 \cos \alpha-\cos (\alpha+\gamma)=\frac{2 \omega L_{B} I_{d}}{\sqrt{2} U_{2}} cosα−cos(α+γ)=2U22ωLBId
题型总结
带漏感的计算
三相桥式不可控整流电路,阻感负载, R = 5 Ω , L = ∞ , U 2 = 220 V R=5 \Omega, \quad L=\infty, \quad U 2=220 V R=5Ω,L=∞,U2=220V
X B = 0.3 Ω ∘ X_{B}=0.3 \Omega_{\circ} XB=0.3Ω∘ 求 U d , I d , I V D , I 2 U_{d}, I_{d}, I_{V D}, I_{2} Ud,Id,IVD,I2 和 γ \gamma γ 的值并作出 u d , i V D u_{d}, i_{V D} ud,iVD 和 i 2 i_{2} i2 的波形。
不可控整流电路就是全控α=0的状况。
U d = 2.34 U 2 cos α − Δ U d Δ U d = 3 X B I d π I d = U d R \begin{array}{l} U_{d}=2.34 U_{2} \cos \alpha-\Delta U_{d} \\ \Delta U_{d}=\frac{3 X_{B} I_{d}} {\pi} \\ I_{d}={U_{d}} {R} \end{array} Ud=2.34U2cosα−ΔUdΔUd=π3XBIdId=UdR
解方程组得:
U d = 2.34 U 2 cos α ( 1 + 3 X B π R ) = 486.9 ( V ) U_{d}=\frac {2.34 U_{2} \cos \alpha }{\left(1+\frac{3 X_{B}} {\pi R}\right)}=486.9(\mathrm{V}) Ud=(1+πR3XB)2.34U2cosα=486.9(V)
I d = 97.38 ( A ) I_{d}=97.38(\mathrm{A}) Id=97.38(A)
∵ cos α − cos ( α + γ ) = 2 I d X B 6 U 2 \because \cos \alpha-\cos (\alpha+\gamma)=\frac{2 I_{\mathrm{d}} X_{\mathrm{B}}} { \sqrt{6} U_{2}} ∵cosα−cos(α+γ)=6U22IdXB
即得出 cos γ = 0.892 \cos \gamma=0.892 cosγ=0.892
换流重叠角 γ = 26.9 3 ∘ \gamma=26.93^{\circ} γ=26.93∘
二极管电流和变压器二次测电流的有效值分别为
I V D = I a 3 = 97.38 3 = 33.46 ( A ) I 2 a = 2 3 I d = 79.51 ( A ) \begin{array}{l} I_{VD}=\frac{I_{a}} {3}=\frac{97.38}{3}=33.46(\mathrm{A}) \\ I_{2 a}=\sqrt{\frac{2}{3}} I_{d}=79.51(\mathrm{A}) \end{array} IVD=3Ia=397.38=33.46(A)I2a=32Id=79.51(A)
选择性查漏补缺
基本概念
整流电路:是电力电子电路中出现最早的一种,将交流电变为直流电的电路。
为什么?
1.输电:远距离输电直流效率更高;
2.负载侧:直流类负载广泛存在。
| 标准 | 分类 |
|---|---|
| 控制 | 不可控,半控,全控 |
| 结构 | 桥式电路,零式电路 |
| 输入相 | 单相电路和多相电路(重点三相) |
| 变压器二次侧电流方向 | 单拍电路和双拍电路 |
单相:一个变压器输入
三相:三角形-星型(变压器一次侧和二次侧)
半波:
桥式:四个,两两一组
不可控:晶闸管
可控:二极管
半控
全控:二极管
| 单相半波可控 | 单相桥式全控 | 三相半波可控整流电路 | 三相桥式全控整流电路 | |
|---|---|---|---|---|
| 移相范围(纯电阻) | 180°/π | 180°/π | 150°/ 5 6 π \frac{5}{6}\pi 65π | 120°/ 2 3 π \frac{2}{3}\pi 32π |
| 移相范围 (阻感) | 90° | 90°/ 1 2 π \frac{1}{2}\pi 21π | 90°/ 1 2 π \frac{1}{2}\pi 21π | 90°/ 1 2 π \frac{1}{2}\pi 21π |
| 输出电压Ud平均值(纯电阻) | 0.45 U 2 1 + cos α 2 0.45 U_{2} \frac{1+\cos \alpha}{2} 0.45U221+cosα | 0.9 U 2 1 + cos α 2 0.9 U_{2} \frac{1+\cos \alpha}{2} 0.9U221+cosα | ||
| 输出电压Ud平均值(阻感) | 0.9 U 2 cos α 0.9 U_{2} \cos \alpha 0.9U2cosα | 0.9 U 2 cos α 0.9 U_{2} \cos \alpha 0.9U2cosα | 1.17 U 2 cos α 1.17 U_{2} \cos \alpha 1.17U2cosα | 2.34 U 2 cos α 2.34U_{2} \cos \alpha 2.34U2cosα |
| I2 | ||||
| I2(阻感) | 2 3 I d = 0.816 I d \sqrt{\frac{2}{3}} I_{d}=0.816 I_{d} 32Id=0.816Id |
输出电流的平均值为: I d = U d R I_{d}=\frac{U_{d}}{R} Id=RUd
单相整流电路
λ = ν λ 1 = I 1 I cos φ 1 = 2 2 π cos α ≈ 0.9 cos α \lambda=\nu \lambda_{1}=\frac{I_{1}}{I} \cos \varphi_{1}=\frac{2 \sqrt{2}}{\pi} \cos \alpha \approx 0.9 \cos \alpha λ=νλ1=II1cosφ1=π22cosα≈0.9cosα
三相整流电路
λ = ν λ I = 1 1 I cos ϕ 1 = 3 π cos α ≈ 0.955 cos α \lambda=\nu \lambda_{I}=\frac{1_1}{I} \cos \phi_{1}=\frac{3}{\pi} \cos \alpha \approx 0.955 \cos \alpha λ=νλI=I11cosϕ1=π3cosα≈0.955cosα
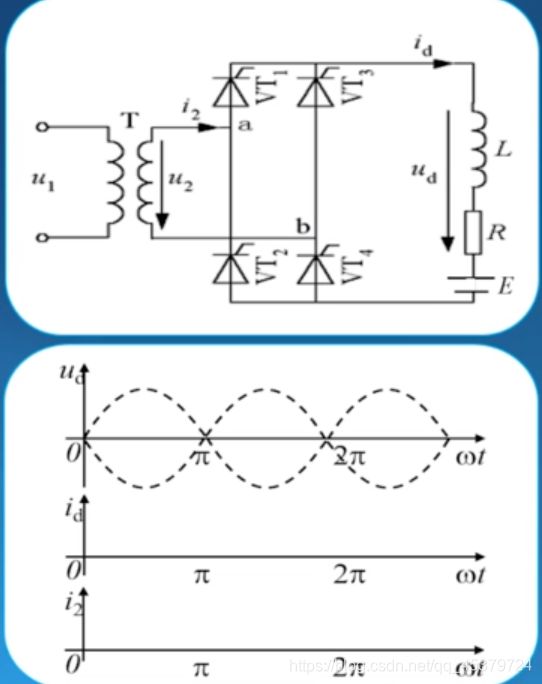
单相半波可控整流电路
基本概念
晶闸管导通的两个条件:
承受正向电压,门级有触发电流
触发延迟角:晶闸管开始承受正向电压起,到施加触发脉冲为止的电角度,用α表示,也称为触发角或控制角。
一个晶闸管
变压器:变换电压和电气隔离,一次侧和二次侧电压瞬时值用u1,u2表示。
晶闸管在分析时视为理想器件(开通和关断瞬时完成)
重点掌握输出电压和负载电流的波形
纯电阻负载
α=0°
意味着在晶闸管开始承受正向电压的时刻,就为晶闸管的门极施加触发脉冲。
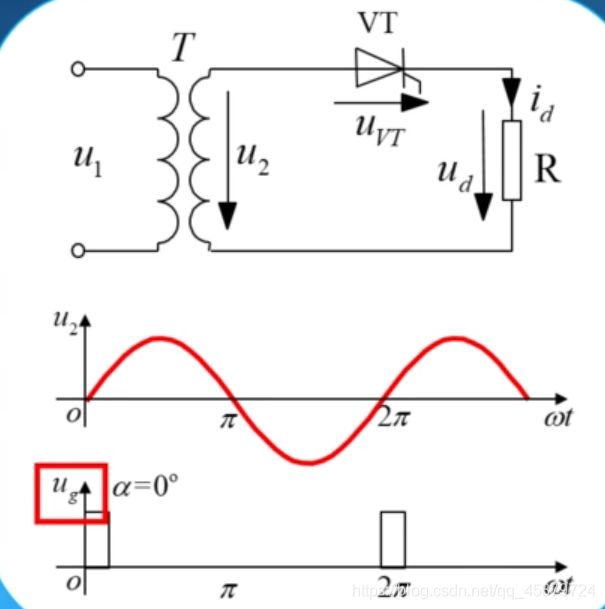
当 ω t = 0 , u d = u 2 , i d = u d R , u ν T = 0 \omega t=0, \quad u_{d}=u_{2}, \quad i_{d}=\frac{u_{d}}{R}, u_{\nu T}=0 ωt=0,ud=u2,id=Rud,uνT=0
当 ω t = π , u 2 = 0 , u d = 0 , i d = 0 \omega t=\pi, \quad u_{2}=0, u_{d}=0, \quad i_{d}=0 ωt=π,u2=0,ud=0,id=0
当 ω t > π \omega t>\pi ωt>π 时,晶闸管承受反向电压,继续关断, u 2 u_{2} u2 全部施加在VT两端, u V T = u 2 u_{V T}=u_{2} uVT=u2
当 ω t = 2 π \omega t=2 \pi ωt=2π 时,晶闸管进入下一个工作周期,重 复上述工作过程。

α=30°
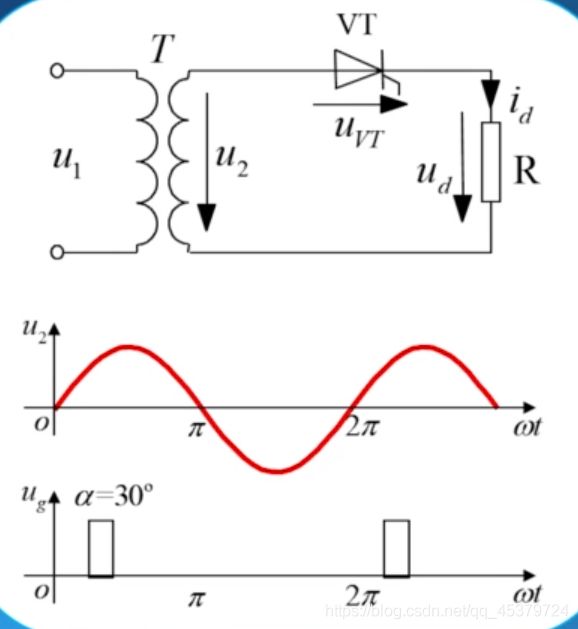
当 ω t = 0 , \omega t=0, ωt=0, 晶闸管开始承受正向电压,但是不 能导通。
当 ω t = 30 ° \omega t=30° ωt=30°。 晶闸管满足导通的条件,开始导通 u d = u 2 , i d = u d R , u V T = 0 u_{d}=u_{2}, i_{d}=\frac{u_{d}}{R}, u_{V T}=0 ud=u2,id=Rud,uVT=0
当 ω t = π \omega t=\pi ωt=π 时 , u 2 = 0 , u d = 0 , i d = 0 , , u_{2}=0, u_{d}=0, i_{d}=0, ,u2=0,ud=0,id=0, 晶闸管关断。
当 ω t = 2 π + 3 0 ∘ \omega t=2 \pi+30^{\circ} ωt=2π+30∘ 时,晶闸管进入下一个工作周期,重复上述工作过程。
Ud的一般公式
U d = 1 2 π ∫ α π 2 U 2 sin ( ω t ) d ( ω t ) = 0.45 U 2 1 + cos α 2 U_{d}=\frac{1}{2 \pi} \int_{\alpha}^{\pi} \sqrt{2} U_{2} \sin (\omega t) d(\omega t)=0.45 U_{2} \frac{1+\cos \alpha}{2} Ud=2π1∫απ2U2sin(ωt)d(ωt)=0.45U221+cosα
触发角α增大,ud的平均值减小。这种输出电压的控制方式称为相位控制方式,简称相控方式。
α=0°时,整流输出平均电压最大;
α=π时,整流输出平均电压为0.
α的移相范围是180°
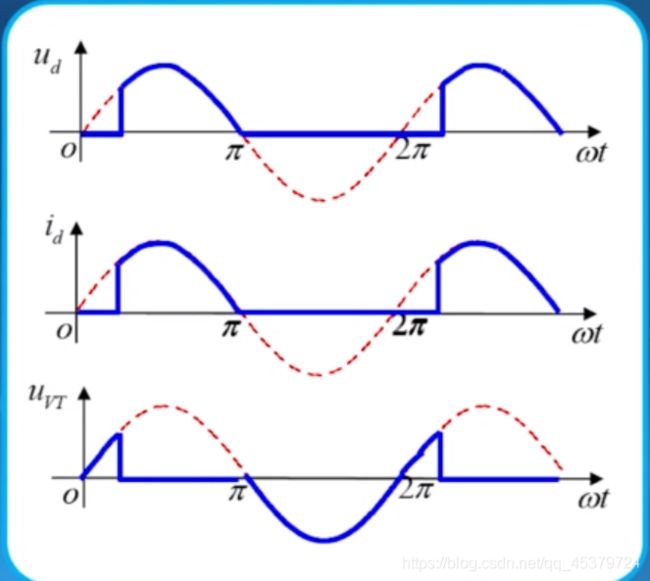
阻感负载
阻感负载的特点是电感对电流变化有抗拒作用,使得流过电感的电流不能发生突变。
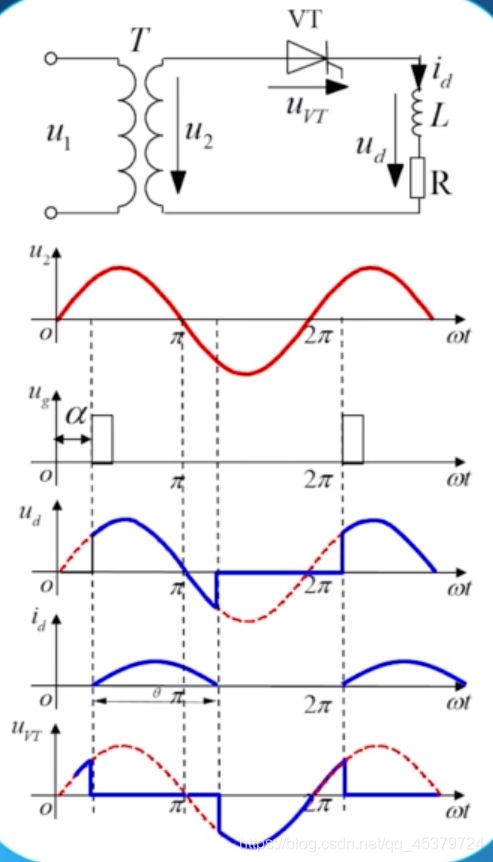
假设触发角为 α \alpha α 时, 晶闸管VT导通
输出电压 u d = u 2 , u_{d}=u_{2}, ud=u2, 由于此时的负载为阻感负载, 负载电流id不能突变,而是从0开始增大。
L d i d d t + R i d = 2 U 2 sin ω t L \frac{\mathrm{d} i_{\mathrm{d}}}{\mathrm{d} t}+R i_{\mathrm{d}}=\sqrt{2} U_{2} \sin \omega t Ldtdid+Rid=2U2sinωt
此时,电感L的感应电动势应阻止电流i 增大,电感L储存能量。
注意π时刻后,电源电压u2等于0,但是电流不为0。甚至电压为负以后,仍然能持续导通。
此时的ud仍等于u2,只是瞬时值为负。
假设当 ω t = θ + α \omega t=\theta+\alpha ωt=θ+α 时, 电感L储存的能量释放完毕, 负载电流 i d = 0 i_{d}=0 id=0 。
L d i d d t + R i d = 2 U 2 sin ω t L \frac{\mathrm{d} i_{\mathrm{d}}}{\mathrm{d} t}+R i_{\mathrm{d}}=\sqrt{2} U_{2} \sin \omega t Ldtdid+Rid=2U2sinωt
代入初始条件: ω t = α , i d = 0 , \omega t=\alpha, i_{d}=0, ωt=α,id=0, 得到
i d = − 2 U 2 Z sin ( α − ϕ ) e − R ω L ( ω t − α ) + 2 U 2 Z sin ( ω t − ϕ ) i_{d}=-\frac{\sqrt{2} U_{2}}{Z} \sin (\alpha-\phi) e^{-\frac{R}{\omega L}(\omega t-\alpha)}+\frac{\sqrt{2} U_{2}}{Z} \sin (\omega t-\phi) id=−Z2U2sin(α−ϕ)e−ωLR(ωt−α)+Z2U2sin(ωt−ϕ)
式中 Z = R 2 + ( ω L ) 2 ϕ = tg − 1 ω L R Z=\sqrt{R^{2}+(\omega L)^{2}} \quad \phi=\operatorname{tg}^{-1} \frac{\omega L}{R} Z=R2+(ωL)2ϕ=tg−1RωL
当 ω t = θ + α \omega t=\theta+\alpha ωt=θ+α 时 , i d = 0 , , i_{d}=0, ,id=0, 于是得到
sin ( α − ϕ ) e − θ tg ϕ = sin ( θ + α − ϕ ) \sin (\alpha-\phi) e^{-\frac{\theta}{\operatorname{tg} \phi}}=\sin (\theta+\alpha-\phi) sin(α−ϕ)e−tgϕθ=sin(θ+α−ϕ)
超越方程
如果触发角α为定值,负载阻抗角φ越大,L储能越多,导通角θ越大,输出电压中负的部分约接近正的部分,平均值ud越接近于0。
带续流二极管
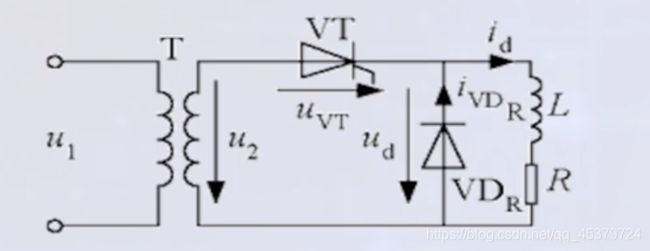
在负载两端并联一个二极管,保证输出 的平均电压为正,用 V D R V D_{R} VDR 表示。

u 2 u_{2} u2 正半周
V T 导 通 , u d = u 2 \mathrm{VT}导通, u_{d}=u_{2} VT导通,ud=u2
V D R \mathrm{VD}_{R} VDR关断,与之前相同
u 2 u_{2} u2 负半周
V D R \mathrm{VD}_{\mathrm{R}} VDR 导通, u d = 0 \quad u_{d}=0 ud=0
使VT关断,电感 L L L 中储存的能量保证电 流 i d i_{d} id 在 L − R − V D R L-R-V D_{R} L−R−VDR 回路中流通,称为续流。
续流期间,输出电压 u d = 0 , u d u_{d}=0, u_{d} ud=0,ud 中不再出现负的部分; 但是负载电流 i d i_d id不为零。如果 电感L足够大,那么在续流期间, V D R VD_{R} VDR 可以持续导通,使i连续,且 i d i_{d} id 的波形接近一条平线。
分析方法总结
分段线性法
将电力电子器件看做理想开关
通态时认为开关闭合,阻抗为0;
断态时认为开关断开,阻抗为无穷大。
线性电路拓扑
器件的每种状态组合对应一种线性电路拓扑,器件通断状态变化时,电路拓扑发生变化。
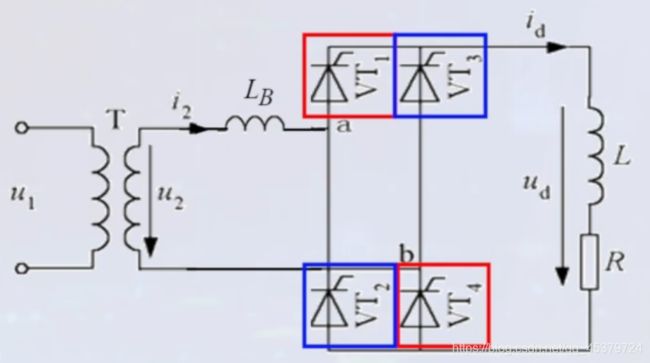
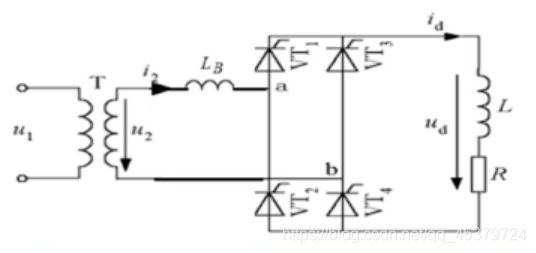
单相桥式全控整流电路
纯电阻负载
![]()
特点:由四个晶闸管组成桥式电路
四个晶闸管分成两组,VT1和VT4,VT2和VT3
每组中的两个晶闸管同时工作
电路输入信号:变压器负边电压u2
电路输出信号:负载端电压ud
学习重点
1.单相桥式全控整流电路的工作原理;
2.画出输出电压ud的波形。
α=0°
自然换相点的确定(用晶闸管替代)
由于需要门级导通,首先要确定自然换相点,触发角α=0的时刻。

自然换相点的确定:用二极管替换四个晶闸管
二极管自然导通的时候,就是自然换相点。
正半周,a点为﹢,b点为-,1,4两个二极管处于正向偏置状态,自然导通。
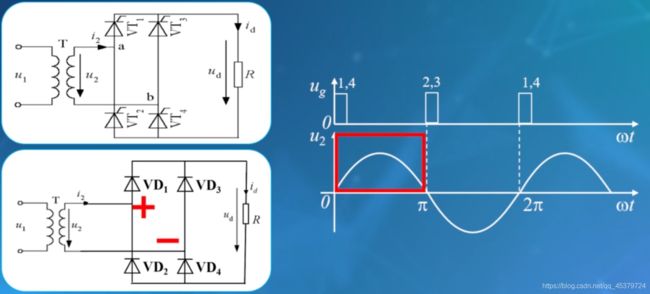
同理,负半周2,3导通。
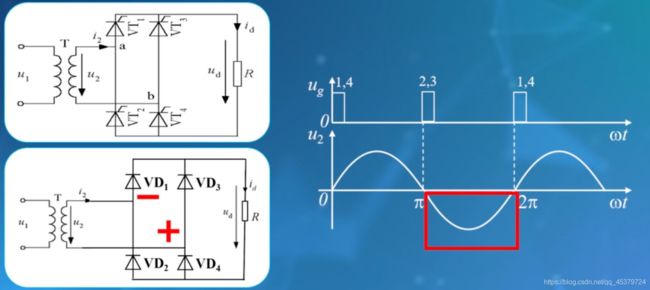
由此可知,晶闸管VT1和VT4的自然换相点是u2正半周过0点,晶闸管VT2和·VT3的自然换相点是u2负半周过0点。
正题
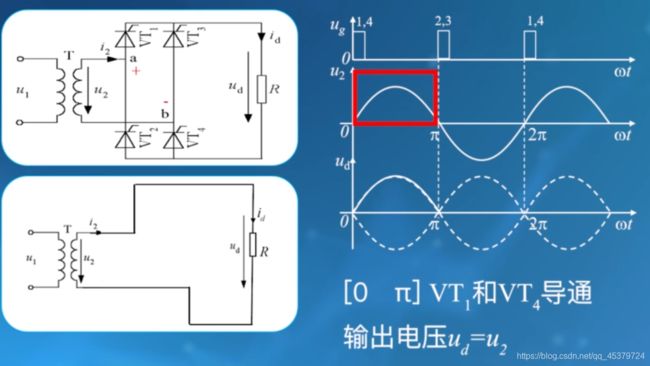

2,3导通时,1,4必然关断,由结构决定。
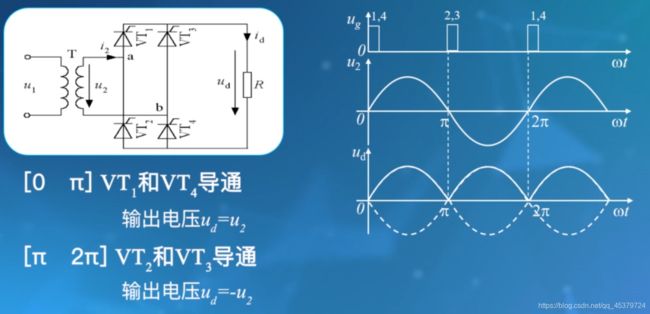
整流电路的作用由此体现出来,将输入电压u2转化为输出电压ud,交流变直流。

负载电流

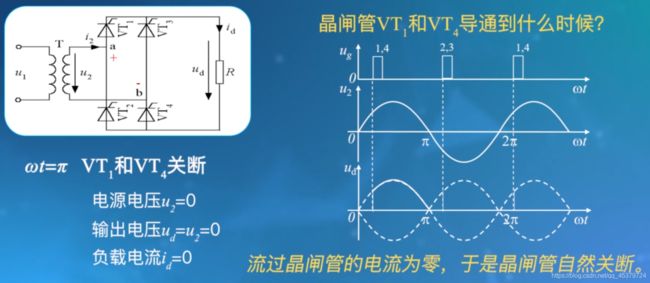
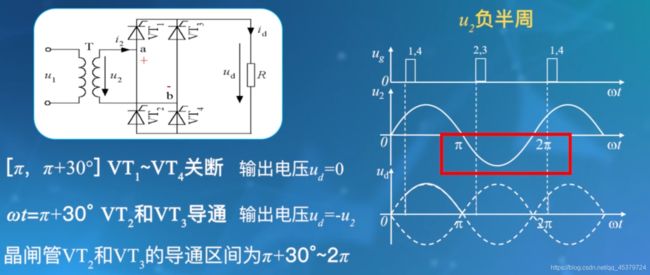
α=30°
晶闸管的触发脉冲出现的时刻位于自然换相点之后的30°
晶闸管VT1和VT4的触发脉冲出现在30°
晶闸管VT2和VT3的触发脉冲出现在π+30°
分析ud波形之前要画出所有触发脉冲

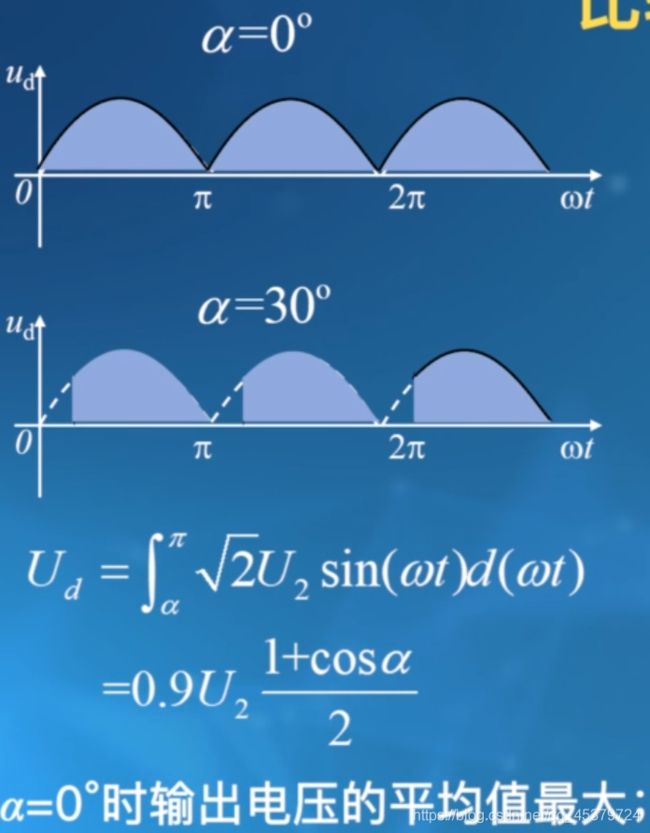
U d = ∫ α π 2 U 2 sin ( ω t ) d ( ω t ) = 0.9 U 2 1 + cos α 2 \begin{aligned} U_{d} &=\int_{\alpha}^{\pi} \sqrt{2} U_{2} \sin (\omega t) d(\omega t) \\ &=0.9 U_{2} \frac{1+\cos \alpha}{2} \end{aligned} Ud=∫απ2U2sin(ωt)d(ωt)=0.9U221+cosα
α = 0 ∘ \alpha=0^{\circ} α=0∘ 时输出电压的平均值最大
移相控制角范围0-180°,180度时,Ud=0。
阻感负载
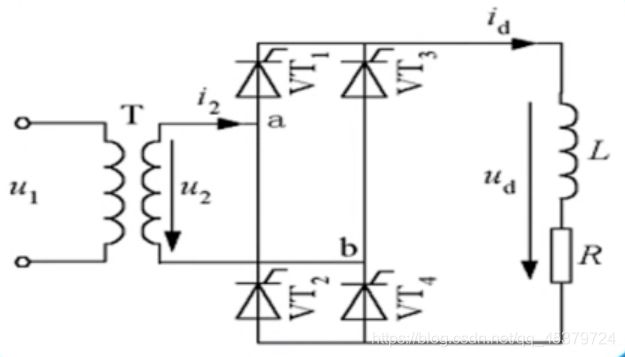
假定L=∞
阻感负载时,电流的特点:id=Id=常数
需要分析输出电压ud,晶闸管VT1两端电压uVT1,电源侧电流i2的波形
设晶闸管的触发角为α,已经知道VT1和VT4自然换相点是正半周过0点,VT2和VT3是负半周过0点
VT1和VT4的触发脉冲出现在ωt=α
VT2和VT3的触发脉冲出现在ωt=π+α
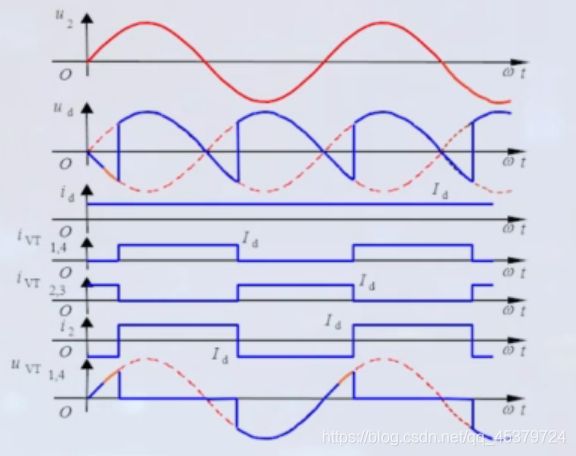
ωt=α时,VT1和VT4导通
ud=u2
uVT1=0
负载id=Id=常数
电源侧i2=Id
ωt=π时,VT1和VT4仍然导通,因为电感L使负载电流恒为常数
ωt=π+α,VT2和VT3导通,VT1和VT4才被迫关断
ud=-u2
uVT1=u2
负载id=Id=常数
电源侧i2=-Id
ωt=2π,u2=0,VT2,VT3导通
ωt=2π+α,VT1,VT4再次导通,VT2,VT3关断
[ a π + α ] V T 1 , V T 4 \left[\begin{array}{ll}a & \pi+\alpha\end{array}\right] \mathrm{VT}_{1}, \mathrm{VT}_{4} [aπ+α]VT1,VT4 导通
u d = u 2 u ν T I = 0 i 2 = I d \begin{array}{l} u_{d}=u_{2} \quad u_{\nu T_{I}}=0 \\ i_{2}=I_{d} \end{array} ud=u2uνTI=0i2=Id
[ π + a 2 π + a ] V T 2 , V T 3 \left[\begin{array}{ll}\pi+a & 2 \pi+a\end{array}\right] \mathrm{VT}_{2}, \mathrm{VT}_{3} [π+a2π+a]VT2,VT3 导通
u d = − u 2 u V T I = u 2 i 2 = − I d u_{d}=-u_{2} \quad u_{V T_{I}}=u_{2}\\ i_{2}=-I_{d} ud=−u2uVTI=u2i2=−Id

输出电压ud与纯电阻负载相比出现了负值,电源侧i2是±各180°的矩形波
整流电路输出电压的平均值
U d = 1 π ∫ α π + α 2 U 2 sin ω t d ( ω t ) U_{\mathrm{d}}=\frac{1}{\pi} \int_{\alpha}^{\pi+\alpha} \sqrt{2} U_{2} \sin \omega t \mathrm{d}(\omega t) Ud=π1∫απ+α2U2sinωtd(ωt)
= 2 2 π U 2 cos α = 0.9 U 2 cos α =\frac{2 \sqrt{2}}{\pi} U_{2} \cos \alpha=0.9 U_{2} \cos \alpha =π22U2cosα=0.9U2cosα
α=0°,ud平均值最大
α=90°,ud平均值0
移相范围是0-90°
晶闸管承受的最大正反向电压为:
U V T max = 2 U 2 U_{V T \max }=\sqrt{2} U_{2} UVTmax=2U2
电源侧电流 i 2 i_{2} i2 的有效值为:
I 2 = I d I_{2}=I_{d} I2=Id
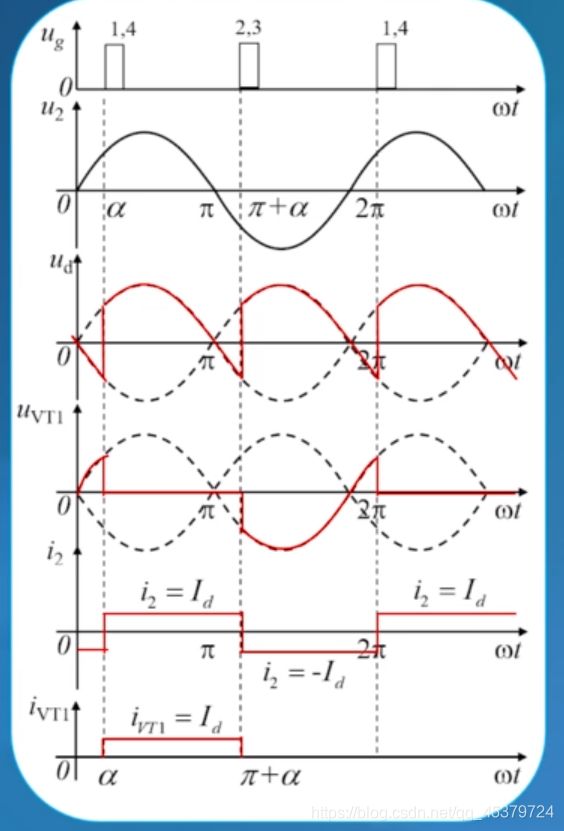
晶闸管VT 1 _{1} 1 的电流平均值为:
I d V T 1 = I d 2 I_{d V T_{1}}=\frac {I_{d}} {2} IdVT1=2Id
晶闸管VT 1 _{1} 1 的电流有效值为:
I V T 1 = I d 2 I_{V T_{1}}=\frac {I_{d}} {\sqrt{2}} IVT1=2Id
反电动势负载
概念:把蓄电池、直流电动机的电枢电压 等看作直流电压源,对于整流电路来说 这样的负载就是反电动势负载。


∣ u 2 ∣ > E \left|u_{2}\right|>E ∣u2∣>E 时,才有晶闸管承受正电压,有导通 的可能。
晶闸管导通之后, u d = u 2 , i d = u d − E R , u_{d}=u_{2},i_{\mathrm{d}}=\frac{u_{\mathrm{d}}-E}{R}, ud=u2,id=Rud−E, 直至 ∣ u 2 ∣ = E \left|u_{2}\right|=E ∣u2∣=E, i d i_{d} id 即降至0使得晶闸管关断,此后 u d = E 。 u_{d}=E_{\text {。 }} ud=E。
与电阻负载时相比,晶闸管提前了电角度 δ \delta δ 停止导电, δ \delta δ 称为停止导电角。
当 α < δ \alpha<\delta α<δ 时,触发脉冲到来时,晶闸管承受负电压,不可能导通。
i d i_{d} id 波形在一周期内有部分时间为0,称为电流断续。
负载为直流电动机时,如果出现电流断续,
电动机的机械特性将很软。(较小的负载电流变换将产生较大的电动机转速变化。)
一般在主电路中直流输出侧串联一个平波电抗器。
通常选取电感量足够大,保证负载电流id连续,那么晶闸管每次导通180°。此时整流电压ud的波形和负载电流id的波形与阻感负载(L=∞)的波形相同,ud的计算公式也一样。
例题
单相桥式全控整流电路, U 2 = 100 V U_2=100V U2=100V,负载中 R = 2 Ω R=2\Omega R=2Ω,L值极大,反电势 E = 60 V , \mathrm{E}=60 \mathrm{V}, E=60V, 当 α = 3 0 ∘ \alpha=30^{\circ} α=30∘ 时,要求:
1. 1. 1. 作出 u d , i d u_{d}, i_{d} ud,id 和 i 2 i_{2} i2 的波形
2. 2. 2. 求整流输出平均电压 U d U_{d} Ud 、电流 I d , I_{d}, Id, 变压器二次侧电流有效 值 I 2 I_{2} I2
3. 3. 3. 考虑安全裕量,确定晶闸管的额定电压和额定电流。

U d = 0.9 U 2 cos α = 0.9 × 100 × cos 3 0 ∘ = 77.97 ( A ) U_{d}=0.9 \mathrm{U}_{2} \cos \alpha=0.9 \times 100 \times \cos 30^{\circ}=77.97(\mathrm{A}) Ud=0.9U2cosα=0.9×100×cos30∘=77.97(A)
I d = ( U d − E ) / R = ( 77.97 − 60 ) / 2 = 9 ( A ) I_{d}=\left(U_{d}-E\right) / \mathrm{R}=(77.97-60) / 2=9(\mathrm{A}) \quad Id=(Ud−E)/R=(77.97−60)/2=9(A)
I 2 = I d = 9 ( A ) I_{2}=I_{d}=9(\mathrm{A}) I2=Id=9(A)
晶闸管承受的最大反向电压为 : 2 U 2 = 100 2 = 141.4 ( V ) : \quad \sqrt{2} U_{2}=100 \sqrt{2}=141.4 (V) :2U2=1002=141.4(V)
流过每个晶闸管的电流的有效值为: I V T = I d / 2 = 6.36 \quad I_{V T}=I_{d} / \sqrt{2}=6.36 IVT=Id/2=6.36
晶闸管的额定电压: U N = ( 2 ∼ 3 ) × 141.4 = 283 ∼ 424 ( V ) \quad U_{N}=(2 \sim 3) \times 141.4=283 \sim 424 (V) UN=(2∼3)×141.4=283∼424(V)
晶闸管的额定电流: I N = ( 1.5 ∼ 2 ) × 6.361.57 = 6 ∼ 8 ( A ) \quad I_{N}=(1.5 \sim 2) \times 6.361 .57=6 \sim 8 (A) IN=(1.5∼2)×6.361.57=6∼8(A)
额定电压和额定电流考虑安全余量
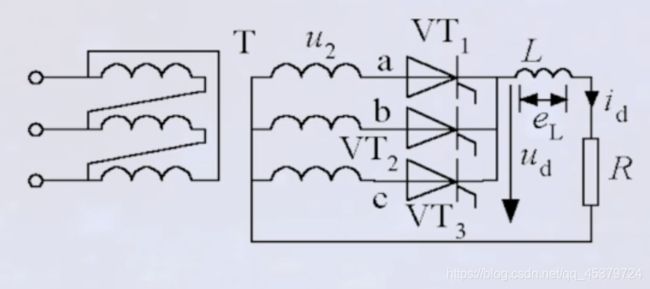
三相半波可控整流电路
整流负载容量较大,直流电压脉动较小,容易滤波时,采用。

结构特点
变压器二次侧接成星型,得到零线,连接负载,一次侧接成三角形,避免3次谐波流入电网。
三个晶闸管共阴极接法连接。
触发电路有公共端,连接方便。
纯电阻负载
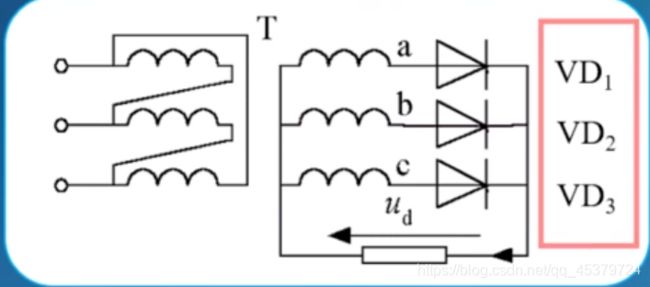
如果是晶闸管,就是三相半波不可控整流电路。哪一个相电压值最大,则该相对应值导通,另外两相由于承受反向电压而关断。
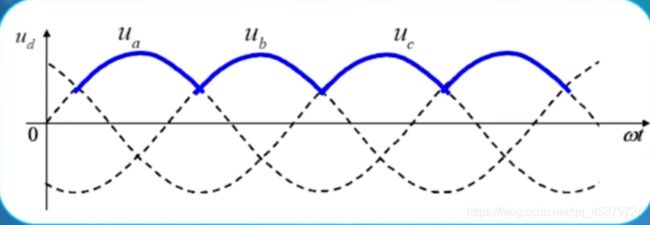
自然换相点:相电压的交点处,均出现二极管换相,称这些交点为自然换相点。
自然换相点是各个晶闸管能触发导通的最早时刻,将其作为触发角α的起点,即α等于0°(对应波形中第一个交点)
α=0°
ω t I ∼ ω t 2 , V T 1 \omega t_{I} \sim \omega t_{2}, \quad \mathrm{VT}_{1} ωtI∼ωt2,VT1 导通 u d = u a , u V T I = 0 u_{d}=u_{a}, \quad u_{V T_{I}}=0 ud=ua,uVTI=0
ω t 2 ∼ ω t 3 , V T 2 \omega t_{2} \sim \omega t_{3}, \quad \mathrm{VT}_{2} ωt2∼ωt3,VT2 导通 u d = u b , u V T I = u a b u_{d}=u_{b}, \quad u_{V T_{I}}=u_{a b} ud=ub,uVTI=uab
ω t 3 ∼ ω t 4 , V T 3 \omega t_{3} \sim \omega t_{4}, \quad \mathrm{VT}_{3} ωt3∼ωt4,VT3 导通 u d = u c , u V T I = u a c u_{d}=u_{c}, \quad u_{V T_{I}}=u_{a c} ud=uc,uVTI=uac
在一个周期中,晶闸管VT1,VT2,VT3轮流导通,各自导通120°ud的波形为三个相电压在正半周的包络线。
α=30°
α=60°
α > 3 0 ∘ \alpha>30^{\circ} α>30∘当导通一相的相电压过零变负时,该相 晶闸管关断,但下一相晶闸管因末触发而不导通, 此时输出电压电流为零。
负载电流断续, 各晶间管导通角小于120。
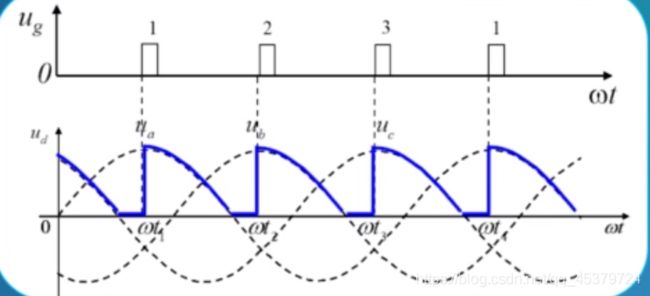
ω t 1 ∼ π , V T 1 导通 u d = u a , u V T I = 0 ω t 2 ∼ π + 2 3 π , V T 2 导通 u d = u b , u V T I = u a b ω t 3 ∼ π + 4 3 π , V T 3 导通 u d = u c , u V T I = u a c \begin{array}{cl}\omega t_{1} \sim \pi, \mathrm{VT}_{1} \text { 导通 } & u_{d}=u_{a}, u_{V T_{I}}=0 \\ \omega t_{2} \sim \pi+\frac{2}{3} \pi, \mathrm{VT}_{2} \text { 导通 } & u_{d}=u_{b}, u_{V T_{I}}=u_{a b} \\ \omega t_{3} \sim \pi+\frac{4}{3} \pi, \mathrm{VT}_{3} \text { 导通 } & u_{d}=u_{c}, u_{V T_{I}}=u_{a c}\end{array} ωt1∼π,VT1 导通 ωt2∼π+32π,VT2 导通 ωt3∼π+34π,VT3 导通 ud=ua,uVTI=0ud=ub,uVTI=uabud=uc,uVTI=uac
α=150°时,整流电压为0。移相范围是0-150°
阻感负载
α=60°
认为电感无穷大
ω t I ∼ ω t 2 , V T 1 \omega t_{I} \sim \omega t_{2}, \quad \mathrm{VT}_{1} ωtI∼ωt2,VT1 导通 u d = u a , u V T I = 0 u_{d}=u_{a}, \quad u_{V T_{I}}=0 ud=ua,uVTI=0
ω t 2 ∼ ω t 3 , V T 2 \omega t_{2} \sim \omega t_{3}, \quad \mathrm{VT}_{2} ωt2∼ωt3,VT2 导通 u d = u b , u V T I = u a b u_{d}=u_{b}, \quad u_{V T_{I}}=u_{a b} ud=ub,uVTI=uab
ω t 3 ∼ ω t 4 , V T 3 \omega t_{3} \sim \omega t_{4}, \quad \mathrm{VT}_{3} ωt3∼ωt4,VT3 导通 u d = u c , u V T I = u a c u_{d}=u_{c}, \quad u_{V T_{I}}=u_{a c} ud=uc,uVTI=uac
仍然各自120°,但是α>30°时,输出电压ud中出现负值。
α=90°,ud正负部分面积相同,平均值为0。
负载电流连续时:
U d = 1 2 π 3 ∫ π 6 + α 5 π 6 + α 2 U 2 sin ω t d ( ω t ) = 3 6 2 π U 2 cos α = 1.17 U 2 cos α \large U_{d}\\ =\frac{1}{\frac{2 \pi}{3}} \int_{\frac{\pi}{6}+\alpha}^{\frac{5 \pi}{6}+\alpha} \sqrt{2} U_{2} \sin \omega t d(\omega t)\\ =\frac{3 \sqrt{6}}{2 \pi} U_{2} \cos \alpha\\ =1.17 U_{2} \cos \alpha Ud=32π1∫6π+α65π+α2U2sinωtd(ωt)=2π36U2cosα=1.17U2cosα
I d = U d R I_{d}=\frac{U_{d}}{R} Id=RUd
I V T = I d 3 I_{V T}=\frac{I_{d}}{\sqrt{3}} IVT=3Id
三相半波整流电路的缺点是,变压器二次电流中含有直流分量,因此应用较少。
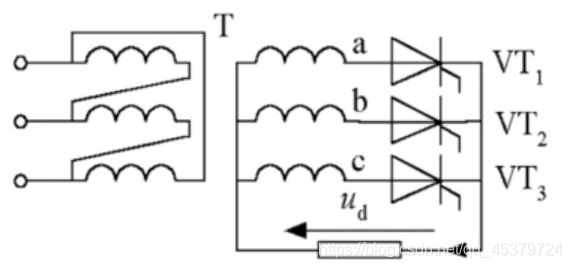
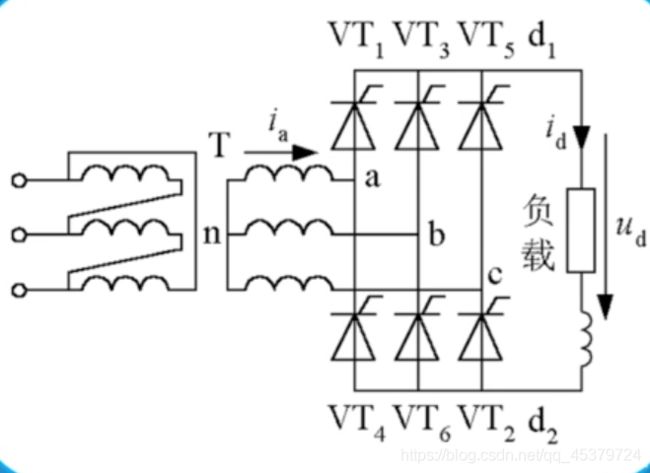
三相桥式全控整流电路
是三相可控整流电路中应用最广的。
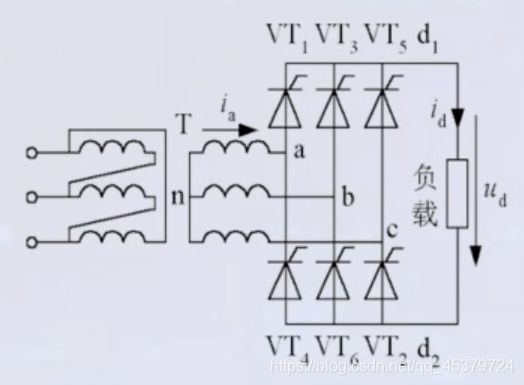
共阴极组: V T 1 , V T 3 , V T 5 \mathrm{VT}_{1}, \mathrm{VT}_{3}, \mathrm{VT}_{5} VT1,VT3,VT5
共阳极组: V T 2 , V T 4 , V T 6 \mathrm{VT}_{2}, \mathrm{VT}_{4} , \mathrm{VT}_{6} VT2,VT4,VT6
注意图中135462的顺序
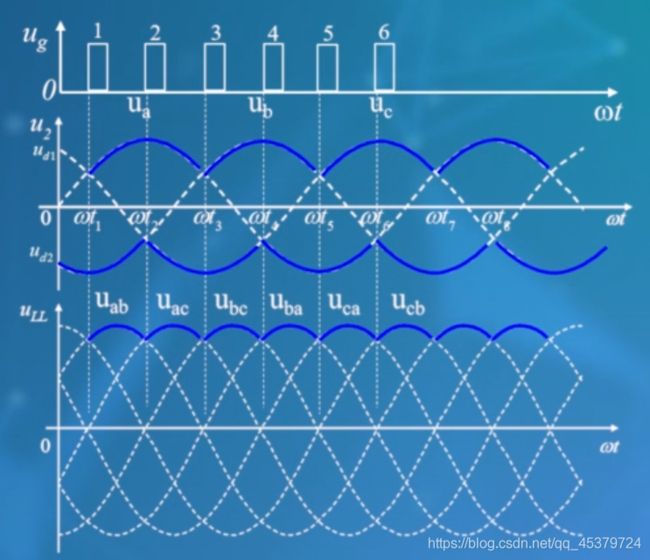
纯电阻负载
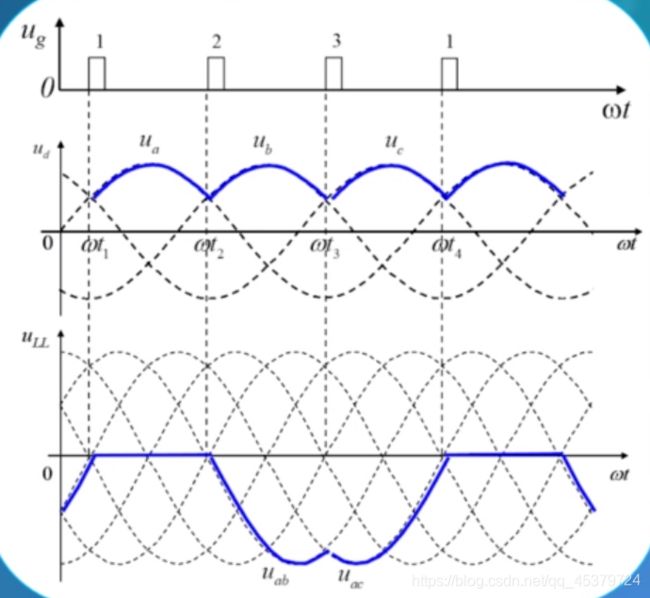
α=0°
纯电阻负载时,三相桥式全控整流电路
的工作过程,画出移相控制角 α = 0 ∘ \alpha=0^{\circ} α=0∘ 时, 输出电压 u d u_{d} ud 的波形。
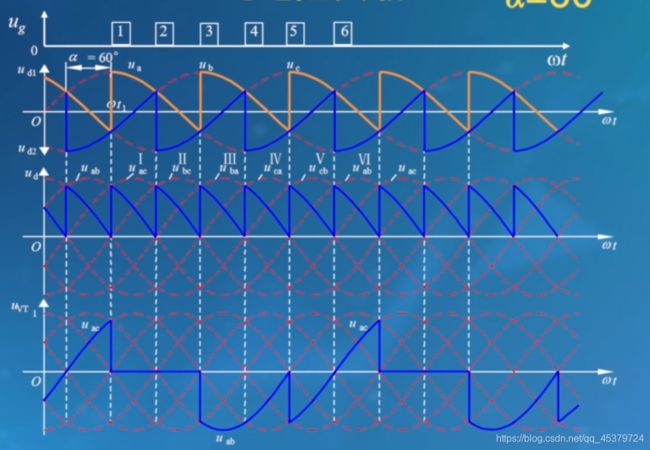
首先确定晶闸管的自然换相点,把晶闸管用二极管代替。共阴极组的3个二极管,阴极电位相同,因此阳极电位最高的自然导通;共阳极组的3个二极管,阳极电位相同,因此阴极电位最高的自然导通。
共阴极组的3个二极管,自然换相点是正半周的相电压交点;共阳极组的3个二极管,自然换相点是负半周的相电压交点。
为了分析方便,通常选取变压器二次侧中点n为参考点,输出电压ud=ud1-ud2。
ω t I ∼ ω t 3 , V T 1 导通 u d I = u a ω t 3 ∼ ω t 5 , V T 3 导通 u d I = u b ω t 5 ∼ ω t 7 , V T 5 导通 u d I = u c \begin{array}{lll}\omega t_{I} \sim \omega t_{3}, & \mathrm{VT}_{1} \text { 导通 } & u_{d I}=u_{a} \\ \omega t_{3}\sim \omega t_{5}, & \mathrm{VT}_{3} \text { 导通 } & u_{d I}=u_{b} \\ \omega t_{5} \sim\omega t_{7}, & \mathrm{VT}_{5} \text { 导通 } & u_{d I}=u_{c}\end{array} ωtI∼ωt3,ωt3∼ωt5,ωt5∼ωt7,VT1 导通 VT3 导通 VT5 导通 udI=uaudI=ubudI=uc
输出电压ud1相电压正半周的包络线
ω t 2 ∼ ω t 4 , V T 2 导通 u d 2 = u c ω ∼ t 4 ω t 6 , V T 4 导通 u d 2 = u a ω t 6 ∼ ω t 8 , V T 6 导通 u d 2 = u b \begin{array}{lll}\omega t_{2} \sim \omega t_{4}, & \mathrm{VT}_{2} \text { 导通 } & u_{d 2}=u_{c} \\ \omega \sim t_{4} \omega t_{6}, & \mathrm{VT}_{4} \text { 导通 } & u_{d 2}=u_{a} \\ \omega t_{6} \sim \omega t_{8}, & \mathrm{VT}_{6} \text { 导通 } & u_{d 2}=u_{b}\end{array} ωt2∼ωt4,ω∼t4ωt6,ωt6∼ωt8,VT2 导通 VT4 导通 VT6 导通 ud2=ucud2=uaud2=ub
输出电压ud2相电压负半周的包络线
接下来将时间区域划分6块
| 时段 | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| 共阴极组中导通的晶闸管 | VT1 | VT1 | VT3 | VT3 | VT5 | VT5 |
| 共阳极组中导通的晶闸管 | VT6 | VT2 | VT2 | VT4 | VT4 | VT6 |
| 整流输出电压ud | ua-ub=uab | ua-uc=uac | ub-uc=ubc | ub-ua=uba | uc-ua=uca | uc-ub=ucb |
然后画出ud,可见ud是线电压正半周的包络线
接下来分析VT1电流电压
i V T I i_{V T_{I}} iVTI
ω t 1 ∼ ω t 3 , V T 1 \omega t_{1} \sim \omega t_{3}, \quad \mathrm{VT}_{1} ωt1∼ωt3,VT1 导通 i V T I = u d R i_{V T_{I}}=\frac{u_{d}} { R} iVTI=Rud
u V T I : u_{V T_{I}}: uVTI:
ω t I ∼ ω t 3 , V T 1 \omega t_{I} \sim \omega t_{3}, \quad \mathrm{VT}_{1} ωtI∼ωt3,VT1 导通 u V T I = 0 u_{V T_{I}}=0 uVTI=0
ω t 3 ∼ ω t 5 , V T 3 \omega t_{3} \sim \omega t_{5}, \quad \mathrm{VT}_{3} ωt3∼ωt5,VT3 导通 u V T I = u a b u_{V T_{I}}=u_{a b} uVTI=uab
ω t 5 ∼ ω t 7 , V T 5 \omega t_{5} \sim \omega t_{7}, \quad \mathrm{VT}_{5} ωt5∼ωt7,VT5 导通 u V T I = u a c u_{V T_{I}}=u_{a c} uVTI=uac
工作特点
- 每个时刻均需两个晶闸管同时导通且不是一侧的
- 触发脉冲按照1-2-3-4-5-6的顺序依次 出现
- 输出电压 u d u_{d} ud 在一个周期内脉动6次且每次波形相同
- 常用双窄脉冲触发。(宽脉冲出发需要电流宽度大于60°,也可以采用双窄脉冲触发,触发二极管时给前一个二极管补发脉冲)
α=30°
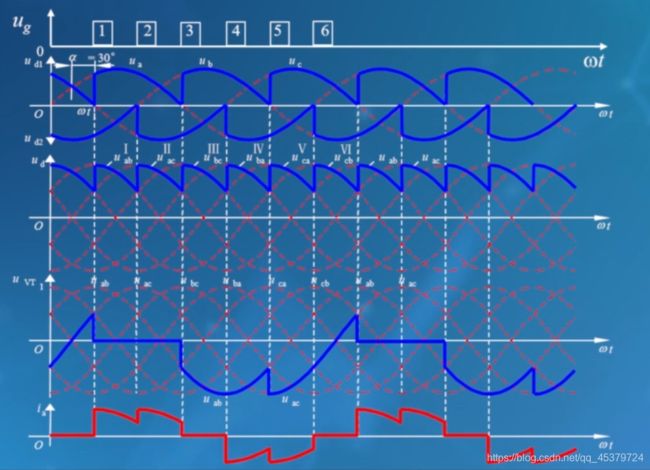
ud不再是线电压正半周的包络线,i·a中,VT1导通时,i·a等于负载电流Ib,VT4导通时,i·a大小还是等于负载电流Ib但是方向相反。
α=60°
α=90°
![]()
ud的波形中每60°有30°为0,ud为0时负载电流也为0,晶闸管关断。ud的波形不会出现负值,α继续增大到120°,则ud始终为0.
阻感负载
三相桥式全控整流电路大多用于向阻感负载和反电动势阻感负载供电。
α<60°
u d u_d ud波形连续,电路的工作情况与纯电阻负载时十分相似,各个晶闸管的通断情况、整流输出电压 u d u_{d} ud 的波形、晶闸管承受的电压波形等都一样。
晶闸管的导通顺序为:1-2-3-4-5-6 ;
各自然换相点:相电压的交点;
每个时刻需要2个晶闸管同时导通
同一相的两个晶闸管不能同时导通。
阻感负载特点:
当电感足够大时,负载电流的波形可以近似为 一条水平线。

α≥60°
纯电阻负载时,输出电压 u a u_{a} ua 不会出现负的部分;
阻感负载时,由于电感L的作用, 负载电流 i i i 恒为常数, 相应的晶闸管持续工作,输出电压 u u u 的瞬时值有可能为负值, 所以 u d u_d ud 的波形中会出现负的部分。
α=90°时
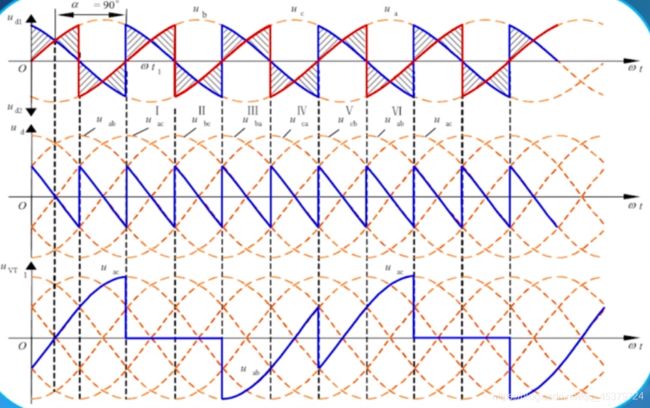
此时ud正负半周的面积相等。阻感负载时, 三相桥式全控整流电路 α \alpha α 角的 移相范围是0 ∘ ∼ 9 0 ∘ ^{\circ} \sim 90^{\circ} ∘∼90∘ 。
α=60°
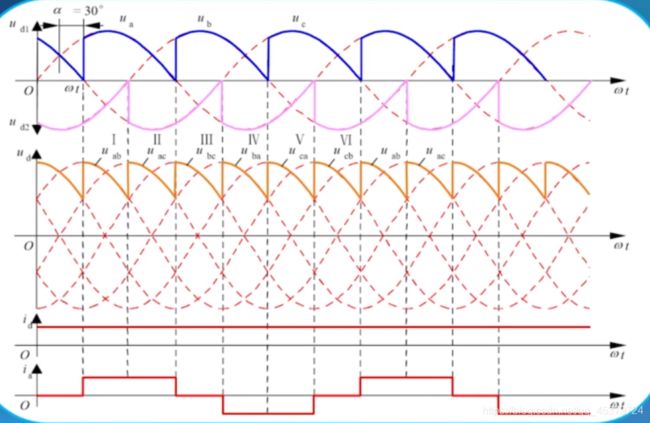
每次脉动相同,只需要分析一个波形,也就是1/6周期。为分析方便,将线电压的过零点作为原点。
整流输出电压连续时的平均值为:
U d = 1 π 3 ∫ π 3 + α 2 π 3 + α 6 U 2 sin ω t d ( ω t ) = 2.34 U 2 cos α U_{d}=\frac{1}{\frac{\pi}{3}} \int_{\frac{\pi}{3}+\alpha}^{\frac{2 \pi}{3}+\alpha} \sqrt{6} U_{2} \sin \omega t d(\omega t)=2.34 U_{2} \cos \alpha Ud=3π1∫3π+α32π+α6U2sinωtd(ωt)=2.34U2cosα
输出电流的平均值为: I d = U d R I_{d}=\frac{U_{d}}{R} Id=RUd
变压器一次侧电流是矩形波,前沿相差180°,其有效值为:
I 2 = 1 2 π ( I d 2 × 2 3 π + ( − I d ) 2 × 2 3 π ) I_{2}=\sqrt{\frac{1}{2 \pi}\left(I_{d}^{2} \times \frac{2}{3} \pi+\left(-I_{d}\right)^{2} \times \frac{2}{3} \pi\right)} I2=2π1(Id2×32π+(−Id)2×32π)
= 2 3 I d = 0.816 I d =\sqrt{\frac{2}{3}} I_{d}=0.816 I_{d} =32Id=0.816Id
反电动势阻感负载
在负载电感L足够大的情况下,负载电流连续, 电路的工作情况与阻感负载的工作情 况相似,电路中各电压、电流波形均相同。(只是输出电流平均值有所不同)
接反电动势阻感负载时,输出电流平均值为:
I d = U d − E R I_{d}=\frac{U_{d}-E}{R} Id=RUd−E
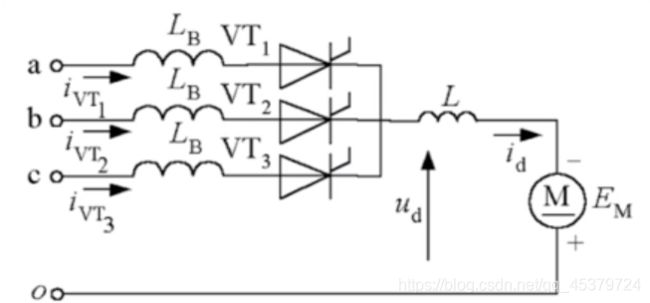
变压器漏感对整流电路的影响
变压器绕组总有漏感,用集中的电感 L B L_{B} LB 表示,并将其折算到变压器二次侧。(由于电感对电流的变化起阻碍作用,电流不能突变,因此换相过程不是瞬时完成)
换相过程持续的时间记作 t γ t_{\gamma} tγ 。
对应的电角度用 γ \gamma γ 表示,称为换相重叠角。
换相也称为换流,就是改变电流的通路。
单相桥式全控整流电路和三相桥式全控整流电路中,换相的过程,变压器漏感对整流输出电压的影响,以及换相重叠角的计算。
假设: 负载中电感很大, 负载电流为常数。
单相桥式全控整流电路
定性分析
不考虑变压器漏感时,电流波形是宽度为180°的矩形波。
考虑漏感时,晶闸管无法瞬时开关。
晶闸管导通和关断需要的时间 t γ t_\gamma tγ
i V T 1 , i V T 4 : 0 → t γ I d i V T 2 , i V T 3 : I d → t γ 0 i 2 : − I d → t γ I d \begin{array}{l} i_{V T_{1}}, i_{V T_{4}}: 0 \stackrel{t_{\gamma}}{\rightarrow} I_{d} \\ i_{V T_{2}}, i_{V T_{3}}: I_{d} \stackrel{t_{\gamma}}{\rightarrow} 0\\ i_{2}:-I_{d} \stackrel{t_{\gamma}}{\rightarrow} I_{d} \end{array} iVT1,iVT4:0→tγIdiVT2,iVT3:Id→tγ0i2:−Id→tγId
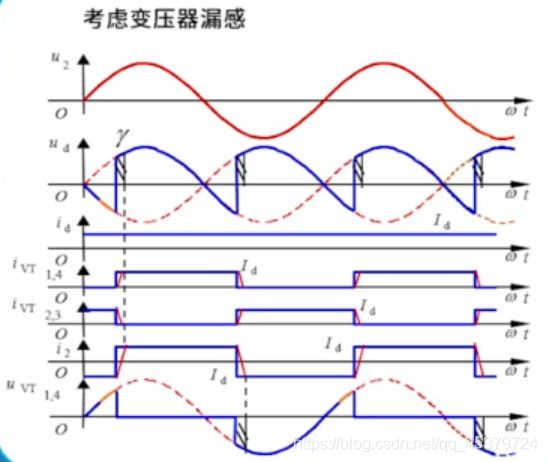
在 t t t 时间内,4个晶闸管全部导通,电路难道不会短路吗?

漏感LB的感应电动势可以保证不短路。

t γ t_\gamma tγ 时间内,4个晶闸管全部导通;
整流电路输出电压 u d u_{d} ud 为零;
相对于 L B L_{B} LB 为零的情况,输出电压 u d u_{d} ud 的波形减少了一部分,输出电压的平均值相应减小;
晶闸管电流的波形在上升沿和下降沿都 不能突变;
电源侧电流i i 2 i_{2} i2 从- I d I_{\mathrm{d}} Id 到I I d I_{\mathrm{d}} Id 的变化也不能突变。
定量计算换相重叠角
T γ T_\gamma Tγ(换相期间),四个晶闸管全部导通,所以整流输出电流为0。
u L B = u 2 u_{L_{B}}=u_{2} uLB=u2漏感感应电动势与电源电压大小相等方向相反。
u L B = L B d i 2 d t = u 2 = 2 U 2 sin ω t u_{L_{B}}=L_{B} \frac{d i_{2}}{d t}=u_{2}=\sqrt{2} U_{2} \sin \omega t uLB=LBdtdi2=u2=2U2sinωt
ω L B d i 2 = 2 U 2 sin ω t d ω t \omega L_{B} d i_{2}=\sqrt{2} U_{2} \sin \omega t d \omega t ωLBdi2=2U2sinωtdωt
∫ − I d I d ω L B d i 2 = ∫ α α + γ 2 U 2 sin ω t d ω t \int_{-I_{d}}^{I_{d}} \omega L_{B} d i_{2}=\int_{\alpha}^{\alpha+\gamma} \sqrt{2} U_{2} \sin \omega t d \omega t ∫−IdIdωLBdi2=∫αα+γ2U2sinωtdωt
cos α − cos ( α + γ ) = 2 ω L B I d 2 U 2 \cos \alpha-\cos (\alpha+\gamma)=\frac{2 \omega L_{B} I_{d}}{\sqrt{2} U_{2}} cosα−cos(α+γ)=2U22ωLBId
Δ U d = 1 π ∫ α α + γ 2 U 2 sin ω t d ω t = 2 ω L B I d π \Delta U_{d}=\frac{1}{\pi} \int_{\alpha}^{\alpha+\gamma} \sqrt{2} U_{2} \sin \omega t d \omega t=\frac{2 \omega L_{B} I_{d}}{\pi} ΔUd=π1∫αα+γ2U2sinωtdωt=π2ωLBId
输出电压ud的周期为π
三相桥式全控整流电路
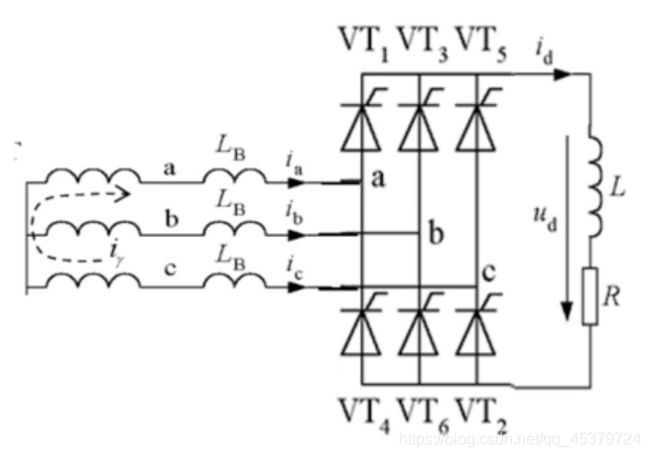
晶闸管 V T 5 VT _{5} VT5 到 V T 1 V T_{1} VT1 的换流,在 t t t 时间内:
晶闸管 V T 5 VT _{5} VT5 关断,电流 i c i_c ic由 I d I_{\mathrm{d}} Id 减小到零
晶闸管 V T 1 VT_1 VT1,导通,电流 i a i_a ia由零增大到I
晶闸管 V T 1 VT _{1} VT1 和 V T 5 \mathrm{VT}_{5} VT5 同时导通, 电源 u d u_{d} ud 和 u c u_{c} uc 通过晶闸管 V T 1 VT_1 VT1,和 V T 5 VT _{5} VT5 构成回路。
也就是说电源侧线电压uac由c相和a相的两个漏感Lc,Lb共同承担。
不考虑变压器漏感 L B , L _{B}, LB, 则 u d I = u a u_{d I}=u_{a} udI=ua 考虑变压器漏感 L B , L _{\mathrm{B}}, LB, 则 u d I < u a u_{d I}
由此可以画出输出电压ud1的变化情况

输出电压ud1将在电源相电压ua的基础上减小一部分。
由于a相漏感LB上的电压,是线电压uac的一半。
L B d i b d t = u b a 2 = 2 2 U L L sin ω t L_{B} \frac{d i_{b}}{d t}=\frac{u_{b a}}{2}=\frac{\sqrt{2}}{2} U_{L L} \sin \omega t LBdtdib=2uba=22ULLsinωt
ω L B d i a = 2 2 U L L sin ω t d ω t \omega L_{B} d i_{\mathrm{a}}=\frac{\sqrt{2}}{2} U_{L L} \sin \omega t d \omega t ωLBdia=22ULLsinωtdωt
∫ 0 I d ω L B d i b = ∫ 5 π 6 + α 5 π 6 + α + γ 2 2 U L L sin ( ω t − 5 π 6 ) d ω t \int_{0}^{I_{d}} \omega L_{B} d i_{b}=\int_{\frac{5 \pi}{6}+\alpha}^{\frac{5 \pi}{6}+\alpha+\gamma} \frac{\sqrt{2}}{2} U_{L L} \sin \left(\omega t-\frac{5 \pi}{6}\right) d \omega t ∫0IdωLBdib=∫65π+α65π+α+γ22ULLsin(ωt−65π)dωt
需要注意的是,等式右侧的被积函数是线电压uac,而波形图是以a相相电压正半周过零点为原点。所以要注意线电压uac的积分上下限。整理之后可以得到换相重叠角。
cos α − cos ( α + γ ) = 2 ω L B I d 2 U L L \cos \alpha-\cos (\alpha+\gamma)=\frac{2 \omega L_{B} I_{d}}{\sqrt{2} U_{L L}} cosα−cos(α+γ)=2ULL2ωLBId
Δ U d = 3 π ∫ π 6 + α π 6 + α + γ 2 2 U L L sin ( ω t − π 6 ) d ω t = 3 π ∫ 0 I d ω L B d i b = 3 ω L B I d π \Delta U_{d}\\ =\frac{3}{\pi} \int_{\frac{\pi}{6}+\alpha}^{\frac{\pi}{6}+\alpha+\gamma} \frac{\sqrt{2}}{2} U_{L L} \sin \left(\omega t-\frac{\pi}{6}\right) d \omega t\\ =\frac{3}{\pi} \int_{0}^{I_{d}} \omega L_{B} d i_{b}\\ =\frac{3 \omega L_{B} I_{d}}{\pi} ΔUd=π3∫6π+α6π+α+γ22ULLsin(ωt−6π)dωt=π3∫0IdωLBdib=π3ωLBId
晶闸管VT 1 _{1} 1 到VT 3 _{3} 3 的换流过程也类似。

L B d i b d t = u b a 2 = 2 2 U L L sin ω t L_{B} \frac{d i_{b}}{d t}=\frac{u_{b a}}{2}=\frac{\sqrt{2}}{2} U_{L L} \sin \omega t LBdtdib=2uba=22ULLsinωt
ω L B d i a = 2 2 U L L sin ω t d ω t \omega L_{B} d i_{\mathrm{a}}=\frac{\sqrt{2}}{2} U_{L L} \sin \omega t d \omega t ωLBdia=22ULLsinωtdωt
∫ 0 I d ω L B d i b = ∫ 5 π 6 + α 5 π 6 + α + γ 2 2 U L L sin ( ω t − 5 π 6 ) d ω t \int_{0}^{I_{d}} \omega L_{B} d i_{b}=\int_{\frac{5 \pi}{6}+\alpha}^{\frac{5 \pi}{6}+\alpha+\gamma} \frac{\sqrt{2}}{2} U_{L L} \sin \left(\omega t-\frac{5 \pi}{6}\right) d \omega t ∫0IdωLBdib=∫65π+α65π+α+γ22ULLsin(ωt−65π)dωt
cos α − cos ( α + γ ) = 2 ω L B I d 2 U L L \cos \alpha-\cos (\alpha+\gamma)=\frac{2 \omega L_{B} I_{d}}{\sqrt{2} U_{L L}} cosα−cos(α+γ)=2ULL2ωLBId
Δ U d = 3 π ∫ π 6 + α π 6 + α + γ 2 2 U L L sin ( ω t − π 6 ) d ω t = 3 π ∫ 0 I d ω L B d i b = 3 ω L B I d π \Delta U_{d}=\frac{3}{\pi} \int_{\frac{\pi}{6}+\alpha}^{\frac{\pi}{6}+\alpha+\gamma} \frac{\sqrt{2}}{2} U_{L L} \sin \left(\omega t-\frac{\pi}{6}\right) d \omega t=\frac{3}{\pi} \int_{0}^{I_{d}} \omega L_{B} d i_{b}=\frac{3 \omega L_{B} I_{d}}{\pi} ΔUd=π3∫6π+α6π+α+γ22ULLsin(ωt−6π)dωt=π3∫0IdωLBdib=π3ωLBId
变压器漏感对整流电路的影响
出现换相重叠角 γ , \gamma, γ, 整流输出电压平均值 U d U_{d} Ud 降低;
整流电路的工作状态增多;
晶闸管的 d i d t \frac{di}{dt} dtdi (电流变化率)减少, 有利于晶闸管的安全开通,有时人为串入进线电抗器以抑制晶闸管的 d i d t \frac{di}{dt} dtdi ;
换相时晶闸管电压出现缺口,产生正的 d u d t \frac{du}{dt} dtdu 可能使晶闸管误导通,为此必须加吸收电路;
换相使电网电压出现缺口,成为干扰源。
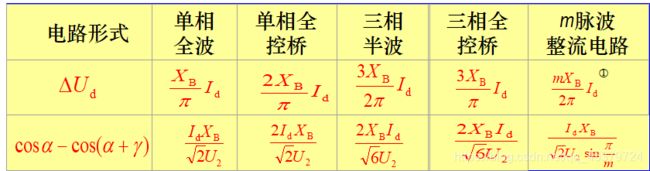
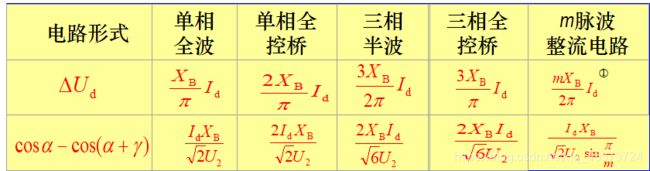
注:(1)单相全控桥电路中,环流 i k i_{\mathrm{k}} ik 是从- I d I_{\mathrm{d}} Id 变为 I d ∘ I_{\mathrm{d} \circ} Id∘ 本表所 列通用公式不适用;
(2)三相桥等效为相电压等于 根号3U2 的6脉波整流 电路,故其 m = 6 , m=6 , m=6, 相电压按根号3U2代入。
电容滤波的不可控整流电路(#####待补充########)
电路结构
直流负载两侧并联电容。
有源逆变(交流侧接电网)
逆变:把直流电转变成交流电的过程。
有源逆变:当交流侧和电网连结时, 称之为有源逆变电路。
无源逆变:变流电路的交流侧不与电网联接,而直接接到负载,即把直流电逆 变为某一频率或可调频率的交流电供给负载,称为无源逆变。
对于可控晶闸管整流电路,满足一定的条件,就可工作于有源逆变。
其电路形式未变,只是电路工作的条件发生了改变。
变流电路: 既可以工作在整流状态又可以工作在逆变状态的电路。
功率
功率=电压*电流
电压, 电流同向时, 功率为正值, 表现
为吸收 (消耗) 功率;
电压、电流反向时, 功率为负值, 表现
为输出功率。
整流电路把交流电变换为直流电,交流功率输出变换为直流功率消耗。
逆变电路是将直流功率输出变换为交流功率。
电机之间的电能流转
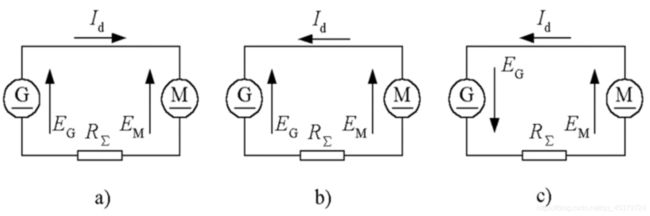
a) 两电动势同极性 E G > E M E_{G}>E_{M} EG>EM
发电机的电压电流反向,输出功率,M作电 动运转,电压电流同向,吸收功率。相当于整流
b) 两电动势同极性 E M > E G E_{M}>E_{G} EM>EG
M在回馈制动状态中,其内电势大于端电压,作发电运转,电流反向, M轴上的机械能转变为电能反送给G。相当于逆变
c) 两电动势反极性,形成短路
电感负载条件下单相整流电压
输出公式: U d = 0.9 U 2 \boldsymbol{U}_{d}=\mathbf{0 . 9} \boldsymbol{U}_{2} Ud=0.9U2 cos α \boldsymbol{\alpha} α
当 a > 9 0 ∘ a>90^{\circ} a>90∘ 时,输出直流电压 U d U_{d} Ud 将变为负值。
由于晶闸管的单向导电性,其电流方向是不会改变的,电压改变,直流侧的功率变为负值。直流侧的功率 (电感储能) 将输出给交流侧 。
直流电变为了交流电,即有源逆变。
实现有源逆变的条件
1 要有直流电动势,其极性须和晶闸管的导通方向一致,其值应大于变流器直流侧的平均电压。
2 要求晶闸管的控制角 α > π 2 , \alpha>\frac{\pi} {2}, α>2π, 使 U d U_{d} Ud 为负值。
以上两者必须同时具备。
必须全控,不能有续流二极管
逆变失败
逆变运行时, 一旦发生换相失败,外接的直流电源就会通过晶闸管电路形成短路,或者使变流器的输出平均电压和直流电动势变成顺向串联,由于逆变电路的内阻很小,形成很大的短路电流。
逆变失败也称为逆变颠覆。
产生原因
1 )触发电路工作不可靠,不能适时、准确地 给各晶闸管分配脉冲,如脉冲丢失、脉冲延时等,致使晶闸管不能正常换相。
2)晶闸管发生故障,该断时不断,或该通时不通。
3)交流电源缺相或突然消失。
4)换相的裕量角不足,引起换相失败。(增加的反向电压时间太短)(前三点是硬件问题,第四点是控制问题)
逆变角(触发角α的补角)
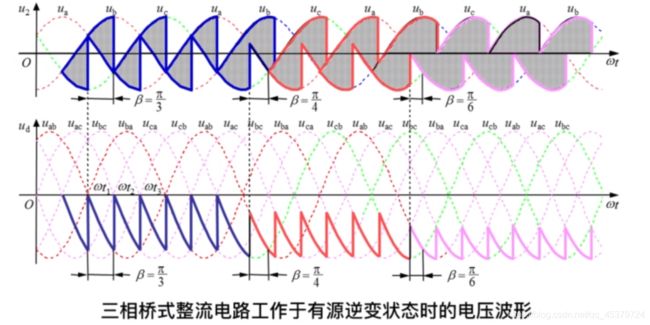
概念:把 a > π / 2 a>\pi / 2 a>π/2 时的控制角用 π − α = β \pi-\alpha=\beta π−α=β 表示,称为逆变角。 β的大小自 β的起始点向左方计量。(图中为有源逆变状态下)原本的起始角始于自然换相点,这里同理,到负半周往左。
变压器抗漏对逆变电路换相的影响
当逆变角 β < γ \beta<\gamma β<γ时,换相尚未结束,电路的工作状态到达自然换相点p点之后, u c \boldsymbol{u}_{c} uc 将高于 u a \boldsymbol{u}_{a} ua, 晶闸管 V T 1 \mathrm{VT}_{1} VT1 承受反压而重新关断,使得应该关断的 V T 3 \mathrm{VT}_{3} VT3 不能关断却继续导通,且c相电压随着时间的推迟愈来愈高,电动势顺向串联导致逆变失败。
当逆变角 β > γ \beta>\gamma β>γ时,经过换相过程后, a相相电压 u a u_{a} ua 仍高于 c c c 相电压 u c , u_{c}, uc, 所以换相结束时,可能使 V T 3 VT_{3} VT3 承受 反压而关断。
避免换相失败βmin
实际上,换相结束之后晶闸管才真正承受反向电压。
晶闸管换相期间承受反压时间的电角度为 : δ = β − γ : \delta=\beta-\gamma :δ=β−γ(200-300微妙,一个周期20毫秒,大概4-5°)
定义: δ \delta δ 为关断角
若 δ ⩾ \delta \geqslant δ⩾ 晶闸管实际关断所需要的时间对应的电角度,则晶闸管就能可靠关断,实现换相。
逆变时允许采用的最小逆变角应等于
β min = δ + γ + θ ′ \boldsymbol{\beta}_{\min }=\boldsymbol{\delta}+\boldsymbol{\gamma}+\boldsymbol{\theta}^{\prime} βmin=δ+γ+θ′
δ是关断角,γ是换相角,θ’是安全裕量角,主要针对脉冲不对称程度(一般可达5°),约取10°。
为避免逆变设计逆变电路失败,必须保证 β ⩾ β m i i n , \beta \geqslant \beta_{m i i n}, β⩾βmiin, 故常在触发电路中附加一保护环节,保证触发脉冲不进入小于 β min \beta_{\min } βmin 的区 域内。
谐波
产生
交流电力系统,传统上是线性系统。线性系统有一个正弦电源或者多个同频率的电源作用时,电路各部分的稳态电压、电流都是同频率的正弦量。
电路中存在非线性元件,如电力电子器件时,即使在正弦电压的作用下,也将产生非正弦的电压和电流。
非线性元件:即使在正弦电源的作用 下,电路中也将产生非正弦周期的电压和电流。
若存在电力电子设备,会使网络的电流波形发生畸变,在网络电流中产生谐波,电压发生畸变。
谐波依然是周期量,是非正弦周期量。
若给定的周期函数满足狄利克雷条件,可展开为傅立叶级数。
将非正弦周期激励电压、电流或信号分解为一系列不同频率的正弦量之和;
根据线性电路的叠加定理,分别计算在各个正弦量单独作用下在电路中产生的同频正弦电流分量和电压分量;
把所得分量按时域形式叠加,得到电路在非正弦周期激初下的稳态电流和电压。
设 f ( t ) f(t) f(t) 为电压或电流的非正弦周期函数,其角频率为 ω ∘ \omega_{\circ} ω∘
f ( t ) = f ( t + k T ) f(t)=f(t+k T) f(t)=f(t+kT)
展开为傅里叶级数:
f ( t ) = F o + ∑ h = 1 ∞ f h ( t ) = 1 2 a o + ∑ h = 1 ∞ [ a h cos ( h ω t ) + b h sin ( h ω t ) ] f(t)=F_{o}+\sum_{h=1}^{\infty} f_{h}(t)=\frac{1}{2} a_{o}+\sum_{h=1}^{\infty}\left[a_{h} \cos (h \omega t)+b_{h} \sin (h \omega t)\right] f(t)=Fo+h=1∑∞fh(t)=21ao+h=1∑∞[ahcos(hωt)+bhsin(hωt)]
正余弦分量从一次到无穷大次。
周期函数的恒定分量为直流分量;
频率为ω的分量为基波分量(h=1);
频率大于1整数倍基波频率的分量称之为谐波分量。(谐波次数h为谐波频率和基波频率的整数比,工频50Hz,三次谐波即150Hz)
危害
- 高次谐波能使电网的电压与电流波形发生畸变,另外相同频率的谐波电压和谐波电流要产生同次谐波的有功功率和无功功率,从而降低电网电压,增加线路损耗,浪费电网容量;
- 影响供电系统的无功补偿设备 ; (谐波进入电网,容易造成变电站高压电容过电流和过负荷,严重时电容会无法正常调节,还有可能进一步放大谐波)
- 影响设备的稳定性,尤其是对继电保护装置, 危害特大(产生误动作);
- 造成异步电动机(感应电动机)效率下降、噪声增大、使低压开关设备产生误动作、对工业企业自动化的正常通讯造成干扰 ;
- 使电力变压器的铜损和铁损增加,直接影响变压器的使用容量和使用效率:
- 造成变压器噪声增加,缩短变压器的使用寿命。
整流电路的谐波分析(交流侧电流)
大电感负载单向桥式
波形分析
大电感负载单向桥式整流电路交流侧电流的谐波分析。
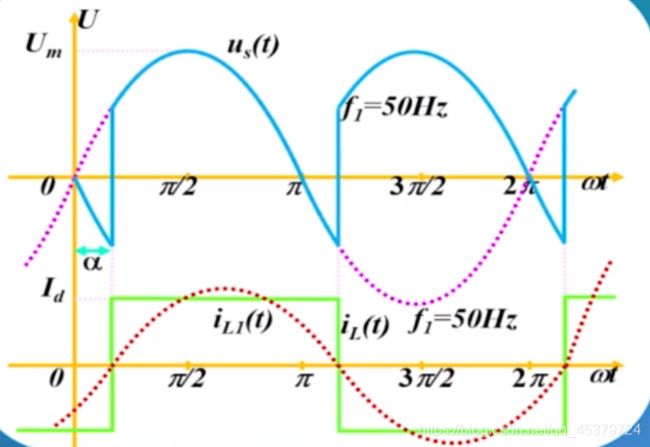
单相晶闸管整流电路输出电压波形和交流侧电流波形如上。
交流侧输入电流i2为绿色方波。
大电感负载的电流波动用傅里叶级数展开:
f ( t ) = i 2 = 4 I d π [ sin ( ω t ) + 1 3 sin ( 3 ω t ) + 1 5 sin ( 5 ω t ) + ⋯ ] f(t)=i_{2}=\frac{4 I_{d}}{\pi}\left[\sin (\omega t)+\frac{1}{3} \sin (3 \omega t)+\frac{1}{5} \sin (5 \omega t)+\cdots\right] f(t)=i2=π4Id[sin(ωt)+31sin(3ωt)+51sin(5ωt)+⋯]
基波,其幅值为: I s 1 m = 4 I d π I_{s 1 m}=\frac{4 I_{d}}{\pi} Is1m=π4Id
基波分量有效值 I s 1 : I s 1 = 2 2 I d π = 0.9 I d I_{s 1}: I_{s_{1}}=\frac{2 \sqrt{2} I_{d}}{\pi}=0.9 I_{d} Is1:Is1=π22Id=0.9Id(幅值除以根号2)
谐波分量有效值 I s h ( h I_{s h}(h Ish(h 为奇数 ) : I s h = I s 1 h ): I_{s h}=\frac{I_{s 1}}{h} ):Ish=hIs1(基波的次数分之1)
基波,交流方波仅含有奇数次谐波,不含 偶数次谐波。 交流电流的谐波次数: h = 3 , 5 , 7 , 9 , 11 , … \mathrm{h}=3,5,7,9,11, \ldots h=3,5,7,9,11,…
电流波形的畸变
电流波形的琦变的大小通过总谐波琦变率THD衡量。
电流的总谐波琦变率为:
T H D i = I ν I s 1 × 100 % = I s 2 − I s 1 2 I s 1 × 100 % = ∑ n = 2 ∞ ( I s h I s 1 ) 2 × 100 % = 48.43 % THD_{i}=\frac{I_{\nu}}{I_{s 1}} \times 100 \%=\frac{\sqrt{I_{s}^{2}-I_{s 1}^{2}}}{I_{s 1}} \times 100 \%=\sqrt{\sum\limits_{n=2}^{\infty}\left(\frac{I_{s h}}{I_{s 1}}\right)^{2}} \times 100 \%=48.43 \% THDi=Is1Iν×100%=Is1Is2−Is12×100%=n=2∑∞(Is1Ish)2×100%=48.43%(理论值,一般会超过这个值)
分母不是总电流的有效值I, 是基波有效值Is1
I ν I_\nu Iν是谐波总有效值,总电流的有效值减去基波有效值,二者平方差值开根号就得到总的有效值。
I ν I_\nu Iν 为总谐波电流,总电流 I 、 I 、 I、 基波电流 I I I_{I} II 、和谐 波电流 I ν I_\nu Iν 之间的关系:
I 2 = I 1 2 + I ν 2 I ν 2 = ∑ h = 2 ∞ I h 2 I^{2}=I_{1}^{2}+I_{\nu}^{2} \quad I_{\nu}^{2}=\sum_{h=2}^{\infty} I_{h}^{2} I2=I12+Iν2Iν2=h=2∑∞Ih2
I 2 = I 1 2 + I 2 2 + I 3 2 + ⋯ + I h 2 ⋯ I^{2}=I_{1}^{2}+I_{2}^{2}+I_{3}^{2}+\cdots+I_{h}^{2} \cdots I2=I12+I22+I32+⋯+Ih2⋯
这是单相整流电路交流侧方波的整流分析。
对于电压来说,由于接入电网,影响不大。
大电感负载三相整流电路
波形分析
大电感负载三相整流电路交流侧电流的谐波分析。

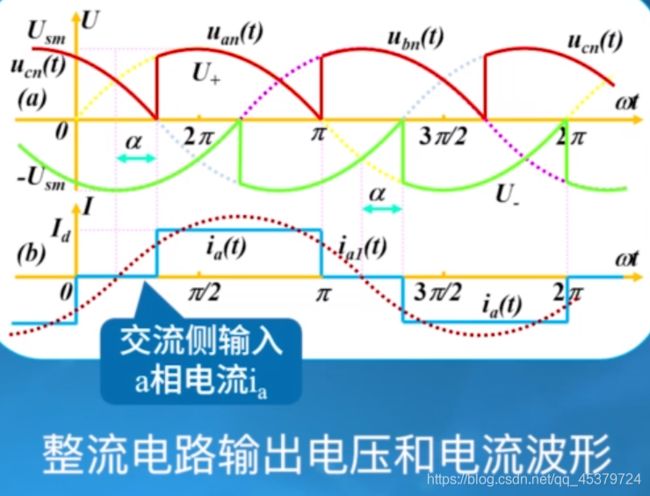
与输入电流单相不同,有缺口
交流侧输入a相电流 i a , i_{a}, ia, 用傅里叶级数展开: i a = 2 3 π I d [ sin ω t − 1 5 sin 5 ω t − 1 7 sin 7 ω t + 1 11 sin 11 ω t + 1 13 sin 13 ω t − ⋯ ] i_{a}=\frac{2 \sqrt{3}}{\pi} I_{d}\left[\sin \omega t-\frac{1}{5} \sin 5 \omega t-\frac{1}{7} \sin 7 \omega t+\frac{1}{11} \sin 11 \omega t+\frac{1}{13} \sin 13 \omega t-\cdots\right] ia=π23Id[sinωt−51sin5ωt−71sin7ωt+111sin11ωt+131sin13ωt−⋯]
基波幅值为: I s 1 m = 2 3 I d π I_{s 1 m}=\frac{2 \sqrt{3} I_{d}}{\pi} Is1m=π23Id
基波分量有效值 I s l : I s 1 = 6 I d π = 0.78 I d I_{s l}: I_{s 1}=\frac{\sqrt{6} I_{d}}{\pi}=0.78 I_{d} Isl:Is1=π6Id=0.78Id
谐 波 分 量 有 效 值 I s h : I s h = I s 1 h 谐波分量有效值 I_{s h}: I_{s h}=\frac{I_{s 1}}{h} 谐波分量有效值Ish:Ish=hIs1((h为奇数,不包含3及3 的整数倍, 且 h = 6 k ± 1 h=6 k \pm 1 h=6k±1, k = 1 , 2 , 3 … … ) k=1,2,3 \ldots \ldots) k=1,2,3……))
该交流方波仅含有奇数次谐波,不含偶数次及3 次和3的整数倍次的谐波(与单相相比,减少了后面的偶次,3次部分,功率因数提高了)。
电流的总谐波畸变率
T H D i = I v I s 1 × 100 % = I s 2 − I s 1 2 I s 1 × 100 % = ∑ h = 2 ∞ ( I s h I s 1 ) 2 × 100 % = 31.08 % T H D_{i}=\frac{I_{v}}{I_{s 1}} \times 100 \%=\frac{\sqrt{I_{s}^{2}-I_{s 1}^{2}}}{I_{s 1}} \times 100 \%=\sqrt{\sum_{h=2}^{\infty}\left(\frac{I_{s h}}{I_{s 1}}\right)^{2}} \times 100 \%=31.08 \% THDi=Is1Iv×100%=Is1Is2−Is12×100%=∑h=2∞(Is1Ish)2