Tensorflow入门(五)——损失函数
上一节
《Tensorflow入门(四)——激活函数》
下一节
《Tensorflow入门(六)——初识卷积神经网络(CNN)》
原文链接:https://my.oschina.net/u/876354/blog/1940819
本文在原文基础上进行细微的修改和完善。
文章目录
-
- 1. 什么是损失函数
- 2. 怎样使用损失函数
-
- 2.1 回归模型的损失函数
- 2.2 分类模型的损失函数
- 2.3 总结
1. 什么是损失函数
损失函数(loss function)是机器学习中非常重要的内容,它是度量模型输出值与目标值的差异,也就是作为评估模型效果的一种重要指标,损失函数越小,表明模型的鲁棒性就越好。
2. 怎样使用损失函数
在TensorFlow中训练模型时,通过损失函数告诉TensorFlow预测结果相比目标结果是好还是坏。在多种情况下,我们会给出模型训练的样本数据和目标数据,损失函数即是比较预测值与给定的目标值之间的差异。
下面将介绍在TensorFlow中常用的损失函数。
2.1 回归模型的损失函数
首先讲解回归模型的损失函数,回归模型是预测连续因变量的。
为方便介绍,先定义预测结果(-1至1的等差序列)、目标结果(目标值为0),代码如下:
import tensorflow as tf
sess = tf.Session()
y_pred = tf.linspace(-1., 1., 100)
y_target = tf.constant(0.)
注意:在实际训练模型时,预测结果是模型输出的结果值,目标结果是样本提供的。
(1)L1正则损失函数(即绝对值损失函数)
L1正则损失函数是对预测值与目标值的差值求绝对值,公式如下:
L ( Y , f ( X ) ) = ∣ Y − f ( X ) ∣ L(Y, f(X))=|Y-f(X)| L(Y,f(X))=∣Y−f(X)∣
在TensorFlow中调用方式如下:
loss_l1_vals = tf.abs(y_pred - y_target)
loss_l1_out = sess.run(loss_l1_vals)
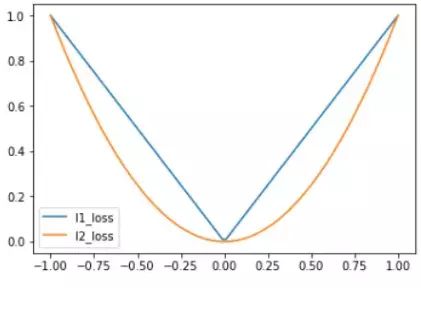
L1正则损失函数在目标值附近不平滑,会导致模型不能很好地收敛。
(2)L2正则损失函数(即欧拉损失函数)
L2正则损失函数是预测值与目标值差值的平方和,公式如下:
L ( Y , f ( X ) ) = ∑ i = 1 n ( Y − f ( X ) ) 2 L(Y, f(X))=\sum_{i=1}^{n}(Y-f(X))^2 L(Y,f(X))=i=1∑n(Y−f(X))2
当对L2取平均值,就变成均方误差(MSE, mean squared error),公式如下:
M S E ( y , y ′ ) = ∑ i = 1 n ( y i − y i ′ ) 2 n MSE(y, y')=\frac{\sum_{i=1}^{n}(y_i-y_i')^2}{n} MSE(y,y′)=n∑i=1n(yi−yi′)2
在TensorFlow中调用方式如下:
# L2损失
loss_l2_vals = tf.square(y_pred - y_target)
loss_l2_out = sess.run(loss_l2_vals)
# 均方误差
loss_mse_vals = tf.reduce.mean(tf.square(y_pred - y_target))
loss_mse_out = sess.run(loss_mse_vals)
L2正则损失函数在目标值附近有很好的曲度,离目标越近收敛越慢,是非常有用的损失函数。
L1、L2正则损失函数如下图所示:
(3)Pseudo-Huber 损失函数
Huber损失函数经常用于回归问题,它是分段函数,公式如下:
L δ ( y , f ( x ) ) = { 1 2 ( y − f ( x ) ) 2 f o r ∣ y − f ( x ) ∣ ≤ δ , δ ∣ y − f ( x ) ∣ − 1 2 δ 2 o t h e r w i s e . L_\delta(y,f(x))=\begin{cases} \frac{1}{2}(y-f(x))^2 & for|y-f(x)|\le\delta,\\ \delta|y-f(x)|-\frac{1}{2}\delta^2 & otherwise. \end{cases} Lδ(y,f(x))={21(y−f(x))2δ∣y−f(x)∣−21δ2for∣y−f(x)∣≤δ,otherwise.
从这个公式可以看出:
当残差(预测值与目标值的差值,即y-f(x) )很小的时候,损失函数为L2范数;残差大的时候,为L1范数的线性函数。
Peseudo-Huber损失函数是Huber损失函数的连续、平滑估计,在目标附近连续,公式如下:
L δ ( a ) = δ 2 ( 1 + ( a / δ ) 2 − 1 ) L_\delta(a)=\delta^2(\sqrt{1+(a/\delta)^2}-1) Lδ(a)=δ2(1+(a/δ)2−1)
该公式依赖于参数delta,delta越大,则两边的线性部分越陡峭。
在TensorFlow中的调用方式如下:
delta = tf.constant(0.25)
loss_huber_vals = tf.mul(tf.square(delta), tf.sqrt(1. + tf.square(y_target - y_pred) / delta) - 1.)
loss_huber_out = sess.run(loss_huber_vals)
L1、L2、Huber损失函数的对比图如下,其中Huber的delta取0.25、5两个值:

2.2 分类模型的损失函数
分类损失函数主要用于评估预测分类结果,重新定义预测值(-3至5的等差序列)和目标值(目标值为1),如下:
y_pred = tf.linspace(-3., 5., 100)
y_target = tf.constant(1.)
y_targets = tf.fill([100, ], 1.)
(1)Hinge损失函数
Hinge损失常用于二分类问题,主要用来评估向量机算法,但有时也用来评估神经网络算法,公式如下:
l ( y ) = max ( 0 , 1 − t ⋅ y ) l(y)=\max(0,1-t\cdot y) l(y)=max(0,1−t⋅y)
在TensorFlow中的调用方式如下:
loss_hinge_vals = tf.maximum(0., 1. - tf.mul(y_target, y_pred))
loss_hinge_out = sess.run(loss_hinge_vals)
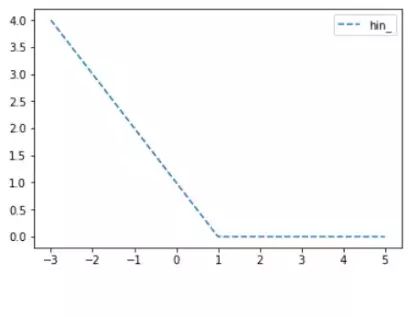
上面的代码中,目标值为1,当预测值离1越近,则损失函数越小,如下图:
(2)两类交叉熵(Cross-entropy)损失函数
交叉熵来自于信息论,是分类问题中使用广泛的损失函数。交叉熵刻画了两个概率分布之间的距离,当两个概率分布越接近时,它们的交叉熵也就越小,给定两个概率分布p和q,则距离如下:
H ( p , q ) = − ∑ x p ( x ) log q ( x ) H(p,q)=-\sum_xp(x)\log q(x) H(p,q)=−x∑p(x)logq(x)
对于两类问题,当一个概率p=y,则另一个概率q=1-y,因此代入化简后的公式如下:
H ( p , q ) = − ∑ i p i log q i = − y log y ^ − ( 1 − y ) log ( 1 − y ^ ) H(p,q)=-\sum_ip_i \log q_i =-y\log \hat{y}-(1-y)\log(1-\hat{y}) H(p,q)=−i∑pilogqi=−ylogy^−(1−y)log(1−y^)
在TensorFlow中的调用方式如下:
loss_ce_vals = tf.mul(y_target, tf.log(y_pred)) - tf.mul((1. - y_target), tf.log(1. - y_pred))
loss_ce_out = sess.run(loss_ce_vals)
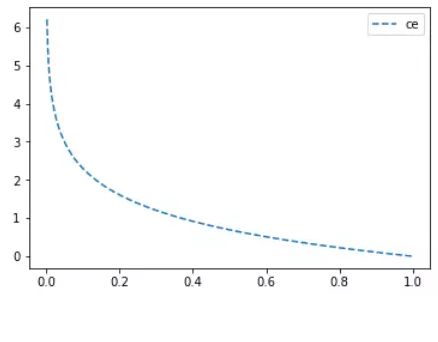
Cross-entropy损失函数主要应用在二分类问题上,预测值为概率值,取值范围为[0,1],损失函数图如下:
(3)Sigmoid交叉熵损失函数
与上面的两类交叉熵类似,只是将预测值y_pred值通过sigmoid函数进行转换,再计算交叉熵损失。在TensorFlow中有内置了该函数,调用方式如下:
loss_sce_vals = tf.nn.sigmoid_cross_entropy_with_logits(y_pred, y_targets)
loss_sce_out = sess.run(loss_sce_vals)
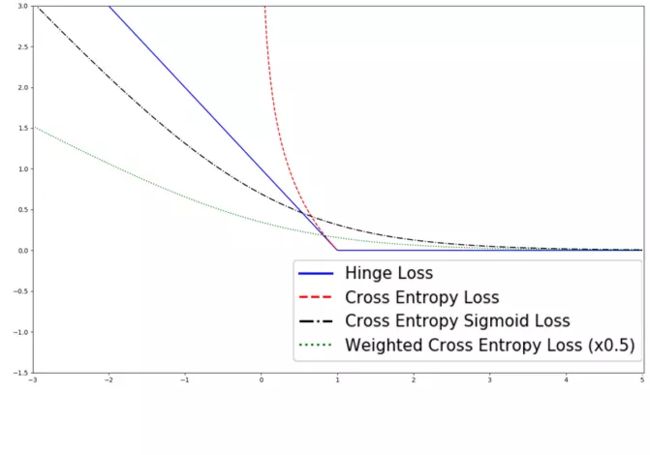
由于sigmoid函数会将输入值变小很多,从而平滑了预测值,使得sigmoid交叉熵在预测值离目标值比较远时,其损失的增长没有那么的陡峭。与两类交叉熵的比较图如下:
(4)加权交叉熵损失函数
加权交叉熵损失函数是Sigmoid交叉熵损失函数的加权,是对正目标的加权。假定权重为0.5,在TensorFlow中的调用方式如下:
weight = tf.constant(0.5)
loss_wce_vals = tf.nn.weighted_cross_entropy_with_logits(y_pred, y_targets, weight)
loss_wce_out = sess.run(loss_wce_vals)
(5)Softmax交叉熵损失函数
Softmax交叉熵损失函数是作用于非归一化的输出结果,只针对单个目标分类计算损失。
通过softmax函数将输出结果转化成概率分布,从而便于输入到交叉熵里面进行计算(交叉熵要求输入为概率),softmax定义如下:
σ ( z ) j = e z j ∑ k = 1 K e z k f o r j = 1 , . . . , K \sigma(z)_j=\frac{e^{z_j}}{\sum_{k=1}^{K}e^{z_k}} \quad\text for \quad j=1,...,K σ(z)j=∑k=1Kezkezjforj=1,...,K
结合前面的交叉熵定义公式,则Softmax交叉熵损失函数公式如下:
L i = − log ( e f y i ∑ j e f j ) or equivalently L i = − f y i + log ∑ j e f j L_i=-\log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) \quad \text{or equivalently} \quad L_i=-f_{y_i}+\log \sum_je^{f_j} Li=−log(∑jefjefyi)or equivalentlyLi=−fyi+logj∑efj
在TensorFlow中调用方式如下:
y_pred = tf.constant([[1., -3., 10.]])
y_target = tf.constant([[0.1, 0.02, 0.88]])
loss_sce_vals = tf.nn.softmax_cross_entropy_with_logits(y_pred, y_target)
loss_sce_out = sess.run(loss_sce_vals)
用于回归相关的损失函数,对比图如下:
2.3 总结
下面对各种损失函数进行一个总结,如下表所示:
| 损失函数 | 使用类型 | 优点 | 缺点 |
|---|---|---|---|
| L1 | 回归 | 更健壮 | 缺少稳定 |
| L2 | 回归 | 更稳定 | 缺少健壮 |
| Psuedo-Huber | 回归 | 更健壮、稳定 | 参数多 |
| Hinge | 分类 | 常用于SVM的最大距离 | 异常值导致无边界损失 |
| Cross-entropy | 分类 | 更稳定 | 缺少健壮、出现无边界损失 |
在实际使用中,对于回归问题经常会使用MSE均方误差(L2取平均)计算损失,对于分类问题经常会使用Sigmoid交叉熵损失函数。
大家在使用时,还要根据实际的场景、具体的模型,选择使用的损失函数。