【算法-LeetCode】718. 最长重复子数组(动态规划)
718. 最长重复子数组 - 力扣(LeetCode)
发布:2021年9月6日16:40:45
问题描述及示例
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
输入:
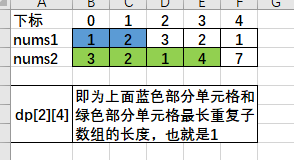
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出:3
解释:
长度最长的公共子数组是 [3, 2, 1] 。
提示:
1 <= len(A), len(B) <= 1000
0 <= A[i], B[i] < 100
我的题解
这里应该最先注意的一个点就是【子数组】和【子序列】的区别,具体一点就是元素是否连续的问题。因为题目没有明确说明,所以我一开始也不敢确定,所以就往评论区瞄了一眼,看是否有人讨论这个问题,没想到第一个评论就是。这里借用题友【@蒲境瑞】的总结:
子序列默认不连续,子数组默认连续。

其实一开始我并没有意识到要用动态规划来做,因为上一道做的LeetCode是滑动窗口的题目,于是我思维惯性地往那个方向开始思考了,虽然后来看到官方题解里确实有滑动窗口的解法,但是很可惜的是我并没有想出思路。所以偷瞄了一眼【相关标签】看到“动态规划”的标签后开始往这个方向思考。但是一开始确定dp的下标含义时就碰了壁,因为一开始我并没有想到是用二维的dp数组解决,后来才尝试着往二维的方向开始思考。
动态规划的套路总结可以参看我此前写的相关博客:
参考:【算法-LeetCode】53. 最大子序和(动态规划初体验)_赖念安的博客-CSDN博客
此前遇到的其他几个动态规划相关题解可以到下方【有关参考】处查看。
我的题解1(动态规划—二维数组)
①根据此前总结的几个动态规划套路。第一步就是要明确 dp 数组的下标含义(我一开始在这里碰了壁,好在后面回过了神)。dp[i][j] 就是指 nums1[0] ~ nums1[i-1] 与 nums2[0] ~ nums2[j-1] 的最长重复子数组的长度。
这里可以思考一下为什么不直接让
dp[i][j]代表nums1[0]~nums1[i]与nums2[0]~nums2[j]的最长重复子数组的长度呢?其实也可以这样表示,但是不方便后续状态转移方程的计算。可以结合后续的分析来体会。
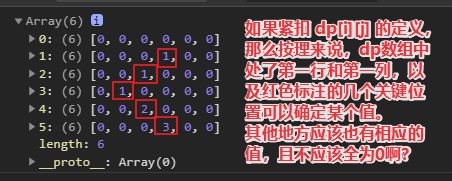
但是要注意的是,下面的程序里并没有体现出当 nums1[i-1] 和 nums2[j-1] 不相等时 dp[i][j] 的值该如何确定,而是将其保持为初始值 0。但是这并不会影响最后的结果,因为我们要求的是连续子数组,当 nums1[i-1] 和 nums2[j-1] 不相等时,我们并不需要考虑将其纳入子数组,但是在理解整个过程时,我们应当明白每一个 dp[i][j] 的取值依据,这样才能对整个动态规划过程有更好的理解。
说实话,在我尝试手动逐步计算
dp[i][j]的值时,我对这道题的理解陷入了难以解释的局面。我根据dp数组的定义手动获得了每个dp[i][j]的值,但是当我将其与控制台输出的dp数组做比较时,我发现我手动计算的结果并不与程序运行结果完全一致。于是我开始怀疑自己是不是对于 dp 数组的下标含义没有理解清楚。这里我卡了很久……
其实出现这个问题的原因就是程序中只在nums1[i-1] === nums2[j-1]时对dp数组的值进行了更新。而这样做已经完全可以满足解题需求了,如果需要把剩余的部分也补充完整的话也可以,但是那属于不必要的冗余代码。
②勉强 弄懂 dp 数组的下标含义后,就要考虑初始化了。这一步我觉得要结合状态转移方程来思考会更好。因为状态转移方程中用到了 nums1[i-1] 和 nums2[j-1] ,所以必须要保证 dp[0][j] (dp数组第一行)和 dp[i][0] (dp数组第一列)有值可取,也就是我们初始化的目标。但是根据dp数组的定义仔细思考 dp[0][j] 和 dp[i][0] 取值却发现它们是无意义的。此时就可以这样看: dp[0][j] 就是指 nums1 为空数组时的情况,此时可以推断 dp[0][j] 应该取 0;dp[i][0] 就是指 nums2 为空数组时的情况,此时可以推断 dp[i][0] 应该取 0。也就是说 dp 数组的第一行和第一列都应该取 0。(也就是上面我手动填充的dp数组中的浅灰色单元格)
③开始考虑状态转移方程。如果当前遍历的 nums1[i-1] 和 nums2[j-1] 相等时,此后可以分为两种情况:
- a、
nums1[i-2]和nums2[j-2]也相等。也就是说明当前遍历的nums1[i-1]和nums2[j-1]的各自的前一位也恰好相等(前缀重复子数组),这时就可以让目标子数组的长度在前缀重复子数组的长度基础上(也就是dp[i-1][j-1])加一,也即是dp[i][j] = dp[i-1][j-1] + 1。 - b、
nums1[i-2]和nums2[j-2]不相等。此时计算子数组长度时就只要考虑当前遍历的nums1[i-1]和nums2[j-1]所组成的子数组长度了,也就是1,即:dp[i][j] = 1。但是恰好此时dp[i-1][j-1]的值恰好为0,所以也可以写成dp[i][j] = dp[i-1][j-1] + 1。
④接下来就是确定遍历顺序了。根据动态转移方程,我们可以知道计算 dp[i][j] 时是从左至右,从上至下逐个计算的。所以可以比较清晰地发现遍历顺序应该是:nums1 和 nums2 都应该由前向后遍历。
一定要注意在每次 dp 数组更新之后都要比较 result 和 dp[i][j] 的大小,并将较大值赋值给 result 。这样才可以保证最后返回结果是最长重复子数组的长度。
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number}
*/
var findLength = function(nums1, nums2) {
// result 用于动态存储nums1和nums2的重复子数组的长度,
// 由于有Math.max,故可以保证程序最后一定可以返回最长的重复子数组长度
let result = 0;
// 创建dp数组并做初始化
let dp = Array.from({length: nums1.length + 1}).map(
() => Array.from({length: nums2.length + 1}).fill(0)
);
// 由前向后遍历nums1数组,注意是从 i=1 开始的
for(let i = 1; i <= nums1.length; i++) {
for(let j = 1; j <= nums2.length; j++) {
if(nums1[i-1] === nums2[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
// 每次dp数组更新之后都要同时更新result的值
result = Math.max(result, dp[i][j]);
}
}
}
return result;
};
提交记录
56 / 56 个通过测试用例
状态:通过
执行用时:1124 ms, 在所有 JavaScript 提交中击败了7.78%的用户
内存消耗:65.9 MB, 在所有 JavaScript 提交中击败了39.52%的用户
时间:2021/09/06 16:42
可以看到这种解法的时间表现和空间表现都不怎么好,如果要优化的话就是通过滚动数组来优化空间消耗。但是在进行数组空间的重复利用时应当注意遍历顺序对取值结果的影响。
我的题解2(暴力解法)
仔细想想的话这道题也还是有暴力解法的。那就是穷举 nums1 中的所有子数组,同时判断其是否为 nums2 的子数组(即判断当前子数组是否为重复子数组),并用一个变量来记录这些重复子数组长度的历史最小值,穷举完 nums1 中的所有子数组后将该变量记录的结果返回。但是之前做那道动态规划的题目时我一开始用的就是暴力解法,结果因为超出时间限制而无法通过,所以这次就不试了。
官方题解
更新:2021年7月29日18:43:21
因为我考虑到著作权归属问题,所以【官方题解】部分我不再粘贴具体的代码了,可到下方的链接中查看。
更新:2021年9月6日16:43:55
参考:最长重复子数组 - 最长重复子数组 - 力扣(LeetCode)
【更新结束】
有关参考
更新:2021年9月6日16:52:50
参考:【算法-LeetCode】53. 最大子序和(动态规划初体验)_赖念安的博客-CSDN博客
参考:【算法-LeetCode】70. 爬楼梯(动态规划入门)_赖念安的博客-CSDN博客
参考:【算法-LeetCode】300. 最长递增子序列(动态规划)_赖念安的博客-CSDN博客
参考:【算法-剑指 Offer】10- I. 斐波那契数列(递归;动态规划)_赖念安的博客-CSDN博客
更新:2021年9月6日23:53:52
参考:「手画图解」动态规划 思路解析 | 718 最长重复子数组 - 最长重复子数组 - 力扣(LeetCode)