【文献阅读笔记】M2MRF: Many-to-Many Reassembly of Features for Tiny Lesion Segmentation in Fundus Images
文章目录
- 摘要
- 1.介绍
- 2、相关工作
-
- 2.1. 深度网络中的特征重组算子
- 2.2. 眼底图像中的微小病变分割
- 2.3. 深度语义分割
- 3. 方法
-
- 3.1. 分析M2ORF运算符
- 3.2. 多对多特征重组(M2MRF)
-
- 3.2.1. 模块概述
- 3.2.2. M2MRF
- 3.2.3. 用于微小病变分割的 M2MRF
- 4. 实验和讨论
-
- 4.1. 实施细节
-
- 4.1.1. 数据集和增强
- 4.1.2. 实验设置
- 4.2. IDRiD数据集上的结果
-
- 4.2.1. 与SOTA的RF上采样算子比较
- 4.2.2. 与SOTA的分割方法的比较
- 5. 结论
摘要
特征重组是现代基于 CNN 的分割方法的重要组成部分,其中包括特征下采样和特征上采样算子。现有的方法将多个特征从一个小的预定义区域独立地为每个目标位置重组一个对应的特征。这可能会导致空间信息丢失,从而使微小病变引起的激活消失,特别是当它们聚集在一起时。
提出的算子many-to-many reassembly of features (M2MRF) 可以减少上述遇到的难题。
(1) 我们的 M2MRF 优于现有的特征重组算子;
(2) 配备 M2MRF,HRNetv2 能够实现比基于 CNN 的分割方法明显更好的性能,并且比最近两种基于 Transformer 的分割方法具有更好的性能。
代码地址: https://github.com/CVIU-CSU/M2MRF-Lesion-Segmentation
2021年12月2日
1.介绍
本文关注的微小病变分割有:
彩色眼底图像中①软渗出物(soft exudates, SEs),②硬渗出物(hard exudates, EXs),③微动脉瘤(microaneurysms, MAs),④出血(hemorrhages, HEs) ,如图1所示:
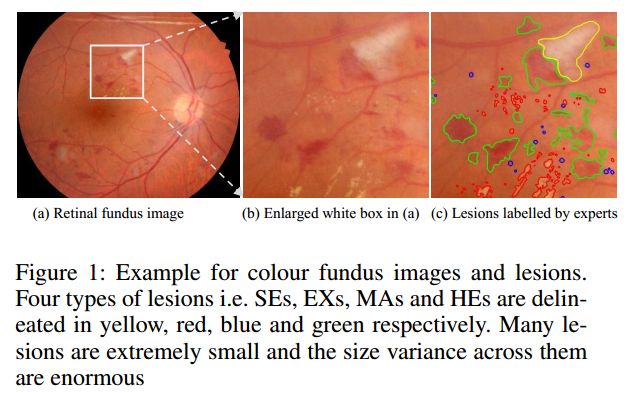
问题:微调的HRNetV2进行眼底图像四类病变分割的mIoU只有47%,这个指标比在自然场景中应用的结果低了很多(19类的Cityscapes的mIoU达到81%)。
可能的原因:两个可能因素是病灶尺寸极小和病灶之间的大规模变化。IDRiD (Porwal et al 2020) 数据集中,尺寸为 4288 × 2848 的图像中,几乎 50% 的病变小于 256 像素。如此微小的病变尺寸对基于 CNN 的分割方法提出了极大的挑战。更糟糕的是,IDRiD 中最小的 10% 病变仅包含不到 74 个像素,而最大的 10% 病变包含超过 1920 个像素。
微小的病变需要 CNN 在较小的感受野内保留尽可能多的局部信息,而大的病变则需要 CNN 在较大的感受野上利用大范围的全局信息。
提出的特征重组(reassembly of features)算子模型应满足:
(1)提升对微小病变的分割;
(2)易于集成到现有的基于CNN的分割模型中。
M2MRF它考虑了微小病变的共存,并通过将大的预定义区域内的多个特征重新组装成多个目标来相互增强其微妙的激活同时具有特征(见图2.b)
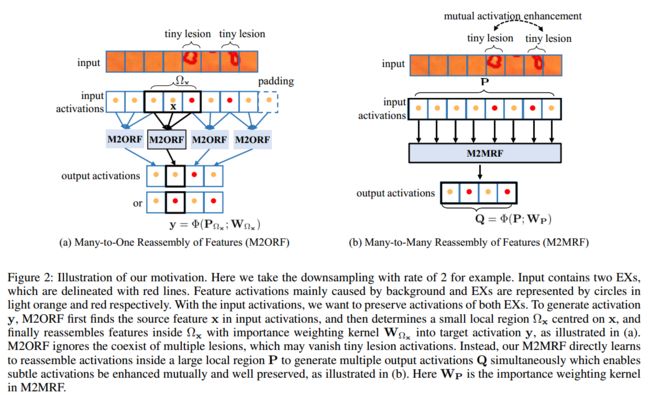
实验证明了 M2MRF 在两个公共微小病变分割数据集上的有效性,即 DDR(Li et al 2019)和 IDRiD(Porwal et al 2020)。实验表明,我们的 M2MRF 的性能优于最先进的特征重组算子。特别是与强大的分割基线 HRNetv2相比,我们的 M2MRF 表现出显着的改进,参数和推理时间的增加可以忽略不计。
2、相关工作
2.1. 深度网络中的特征重组算子
在现有的深度网络中:
(1)广泛采用的特征下采样算子:
①strided max-pooling(跨步最大池化);②strided convolution(跨步卷积)。
(2)广泛采用的特征上采样算子:
①Bilinear interpolation(双线性插值);②deconvolution(反卷积)③unpooling(反池化)
这些算子的总体思想是通过使用重要性核(importance kernels)在预定义区域内重新组装多个特征来为每个目标位置生成特征向量。特别是,用于跨步最大池化、非池化和双线性插值的重要性内核是手工制作的,并且特征图可以逐通道高效地处理。然而,他们忽略了跨通道的上下文依赖性和本地模式(local patterns)的多样性。相反,跨步卷积和反卷积的重要性内核,它们的维度取决于输入特征,在 CNN 中输入特征总是很高。当使用重要度较高的内核时,这使得重组的计算负担很重。因此很难从大区域重新组装特征。
然而最近提出的特征重组算子仍然遵循多对一特征重组(many-to-one feature reassembly, M2ORF)的范式,并且容易稀释甚至消失微小病变的特征。
2.2. 眼底图像中的微小病变分割
该分割从手工制作特征(或深度学习提取的特征)的单一类别病变分割发展成多类病灶分割。例如,在(Li et al 2019)中,PSPNet(Zhao et al 2017)和DeeplabV3+(Chen et al 2018)直接针对多类型病变分割进行微调。 Guo 等人(Guo et al 2019)在 FCN 之上开发了一个名为 L-Seg 的网络(Long、Shelhamer 和 Darrell 2015)。最近,多任务学习框架(Foo et al 2020)(Wang et al 2021b)被提出来利用病变分割和其他任务之间的相关性来提高所有任务的性能。但是上述方法都是采用 many-to-one RF operators,容易忽略病灶中的微小病变。
2.3. 深度语义分割
深度语义分割发展主要可分为三条。
(1)第一条思路重点关注如何生成和聚合多尺度表示。FCN(Long、Shelhamer 和 Darrell 2015)提供了一种自然的解决方案,它重用中层特征来补偿高层特征中的空间细节。UNet (Ronneberger, Fischer, and Brox 2015) 通过跳跃连接将低层信息传播到高层信息,这也激发了许多专门用于医学图像分割的变体,例如 VNet (Milletari, Navab, and Ahmadi 2016)、UNet++ (Zhou et al 2019)、MNet(Fu et al 2018)和 SAN(Liu et al 2019)。在(Li et al 2020)中,提出了门控完全融合(gated fully fusion)来选择性地融合多级特征。
(2)第二条路线侧重于高分辨率表示学习。例如,在(Ronneberger, Fischer, and Brox 2015; Noh, Hong, and Han 2015; Badrinarayanan, Kendall, and Cipolla 2017)中,采用编码器-解码器架构风格来逐渐恢复特征分辨率,而HRNet (Sun et al 2019) ; Wang et al 2020)是专门为学习高分辨率表示而设计的。
(3)第三条路线引入注意力机制和变体模块,例如 DANet (Fu et al 2019)、DRANet (Fu et al 2020)、CCNet (Huang et al 2019)、RecoNet(Chen 等人 2020)、HANet(Choi、Kim 和 Choo 2020)和 DNL(Yin 等人 2020)是为了探索远程依赖而开发的。最近,vision transformer,如 Swin (Liu et al 2021b)、Twins (Chu et al 2021)和 CSWin(Dong et al 2021)是为分割而开发的。然而,这些方法是为了将对象分割为适当的尺寸而不是微小的尺寸而设计的。
3. 方法
- 首先,分析M2ORF运算符
- 然后,详细介绍M2MRF运算符
- 最后,以HRNetV2为例,将M2MRF集成到CNN架构中,完成微小病变的分割。
3.1. 分析M2ORF运算符
输入特征图 X ∈ R H × W × C X\in R^{H×W×C} X∈RH×W×C,采样率 δ \delta δ( δ > 0 \delta >0 δ>0),特征重组的目标是生成目标特征图 Y ∈ R ⌊ δ H ⌋ × ⌊ δ W ⌋ × C Y∈R^{\lfloorδH\rfloor×\lfloorδW\rfloor×C} Y∈R⌊δH⌋×⌊δW⌋×C, Y Y Y由重要性核(importance kernels) W W W参数化的函数映射 Φ \Phi Φ 求得:
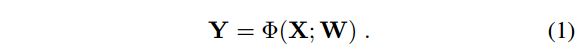
这里的 δ < 1 \delta<1 δ<1为下采样; δ > 1 \delta>1 δ>1为上采样。
为了使特征重组计算高效,大多数现有方法将其降级为多对一局部采样问题,即将预定义局部区域中的多个特征重新组装为一个目标特征。具体来说,对于 Y Y Y中位置 ( i ′ i' i′ , j ′ j' j′ ) 处的目标特征 y ∈ R C y∈R^C y∈RC ,大多数现有方法都假设 X X X 中位置 ( i i i, j j j) 处存在对应的源特征 x ∈ R C x∈R^C x∈RC ,其中 i i i = ⌊ i ′ / δ ⌋ \lfloor i'/δ \rfloor ⌊i′/δ⌋和 j j j = ⌊ j ′ / δ ⌋ \lfloor j'/δ \rfloor ⌊j′/δ⌋。它们按照三个步骤来获得 y :
(1) 根据 x ∈ R C x∈R^C x∈RC, 设置/学习局部区域 Ω x Ω_x Ωx ;
(2)以 Ω x Ω_x Ωx,设定/学习对应的重要性核 W i ′ , j ′ W_{i',j'} Wi′,j′ ;
(3) 得到 y y y,通过下面公式:

其中, P Ω x P_{Ω_x} PΩx表示在 Ω x Ω_x Ωx里的特征。
显然,M2ORF算子假设 Y Y Y 中的每个目标特征是独立的,并且忽略了多个病变的共存。此外,考虑到计算效率,以前的 RF 算子,如跨步卷积、反卷积、CARAFE++ (Wang et al 2021a) 和 A 2 ^2 2U (Dai, Lu, and Shen 2021) 通常考虑小尺寸 Ω x Ω_x Ωx,这使得它们无法利用长范围依赖。结果,微小病变引起的激活很容易被稀释甚至消失。为了减轻微小病变激活的稀释,一种自然的解决方案是放弃 M2ORF 的假设,并同时为多个目标位置生成多个特征,其中的特征位于较大的局部区域内。为此,我们提出多对多特征重组(M2MRF)。
3.2. 多对多特征重组(M2MRF)
3.2.1. 模块概述
图3表明输入特征图 X ∈ R H × W × C X\in R^{H×W×C} X∈RH×W×C经过采样率为 δ \delta δ 的M2MRF算子,得到输出特征图 Y ∈ R ⌊ δ H ⌋ × ⌊ δ W ⌋ × C Y∈R^{\lfloorδH\rfloor×\lfloorδW\rfloor×C} Y∈R⌊δH⌋×⌊δW⌋×C。

(1)首先,对输入特征图 X X X进行通道压缩,使其通道数由 C C C到 C r \frac{C}{r} rC,以提高计算效率,输出记为 X C C X_{CC} XCC。
(2)然后,将 X C C X_{CC} XCC划分为大小为 S h × S w × C r S_h×S_w×\frac{C}{r} Sh×Sw×rC的多个特征块{ P l P_l Pl} l = 1 L _{l=1}^L l=1L,这里 L = ⌊ H / S h ⌋ ⋅ ⌊ W / S h ⌋ L=\lfloor H/S_h\rfloor·\lfloor W/S_h\rfloor L=⌊H/Sh⌋⋅⌊W/Sh⌋。
(3)对每个特征块进行M2MRF操作,输出大小为 ⌊ δ H ⌋ × ⌊ δ W ⌋ × C r \lfloor \delta H\rfloor×\lfloor \delta W\rfloor×\frac{C}{r} ⌊δH⌋×⌊δW⌋×rC的{ Q l Q_l Ql} l = 1 L 的特征块 _{l=1}^L的特征块 l=1L的特征块。
(4)之后,这些特征块被合并成大小为 ⌊ δ H ⌋ × ⌊ δ W ⌋ × C r \lfloor \delta H\rfloor×\lfloor \delta W\rfloor×\frac{C}{r} ⌊δH⌋×⌊δW⌋×rC的特征图 Y C C Y_{CC} YCC。
(5)最后,经过通道恢复(channel recover)将特征通道变为 C C C。
通道压缩和通道恢复操作只需使用1×1的常规卷积即可完成
3.2.2. M2MRF
局部特征块由 P ∈ P∈ P∈{ P l P_l Pl} l = 1 L _{l=1}^L l=1L,生成尺寸大小为 ⌊ δ S h ⌋ × ⌊ δ S w ⌋ × C r \lfloor \delta S_h\rfloor×\lfloor \delta S_w\rfloor×\frac{C}{r} ⌊δSh⌋×⌊δSw⌋×rC的 Q Q Q:
![]()
令 M = ⌊ δ S h ⌋ × ⌊ δ S w ⌋ M=\lfloor \delta S_h\rfloor×\lfloor \delta S_w\rfloor M=⌊δSh⌋×⌊δSw⌋, N = ⌊ S h ⌋ × ⌊ S w ⌋ N=\lfloor S_h\rfloor×\lfloor S_w\rfloor N=⌊Sh⌋×⌊Sw⌋,可以把任务看作为:从含有 N N N个源特征 P = P= P={ x n x_n xn} n = 1 N _{n=1}^N n=1N生成 M M M个特征的 Q = Q= Q={ y m y_m ym} m = 1 M _{m=1}^M m=1M,这里 y m , x n ∈ R 1 × C r y_m,x_n∈R^{1×\frac{C}{r}} ym,xn∈R1×rC。为了实现该任务,一个方法是采用线性映射,因此公式(3)可以改写成:

其中 W 1 , ⋅ ⋅ ⋅ , W M W_1,···,W_M W1,⋅⋅⋅,WM是要学习的参数,其的尺寸大小为 N C r × C r \frac{NC}{r}×\frac{C}{r} rNC×rC。所以 W p a t c h = [ W 1 , ⋅ ⋅ ⋅ , W M ] W_{patch}=[W_1,···,W_M] Wpatch=[W1,⋅⋅⋅,WM]的尺寸大小为 N C r × M C r \frac{NC}{r}×\frac{MC}{r} rNC×rMC。简单起见,可以表示 p = [ x 1 , ⋅ ⋅ ⋅ , x N ] , q = [ y 1 , ⋅ ⋅ ⋅ , y M ] p=[x_1,···,x_N],q=[y_1,···,y_M] p=[x1,⋅⋅⋅,xN],q=[y1,⋅⋅⋅,yM],公式(4)可改写为:
![]()
为了利用远程依赖关系, S h S w S_hS_w ShSw 需要很大。因此,N 和 M 很大并且 W p a t c h W_{patch} Wpatch 将是一个很大的矩阵。一方面,优化如此大的矩阵总是很困难;另一方面,存储大矩阵会导致高内存消耗。为了减少要学习的参数数量,论文通过两层线性投影将 W p a t c h W_{patch} Wpatch 分解为两个小矩阵。因此公式 (4) 可以改写为:
![]()
其中, W P ′ ∈ R N C r × N C α r W'_P∈R^{\frac{NC}{r}×\frac{NC}{αr}} WP′∈RrNC×αrNC, W P ′ ′ ∈ R N C α r × M C r W''_P∈R^{\frac{NC}{αr}×\frac{MC}{r}} WP′′∈RαrNC×rMC是两个线性投影中的参数。α ≥ 1 \geq1 ≥1,使得 W P ′ W'_P WP′和 W P ′ ′ W''_P WP′′矩阵的维度远小于 W p a t c h W_{patch} Wpatch。
3.2.3. 用于微小病变分割的 M2MRF
由于 HRNetV2(Wang et al 2020)最初是为高分辨率表示学习而设计的,并且在语义分割任务上取得了最先进的性能,因此采用它作为微小病变分割的基线。
在 HRNetV2(Wang et al 2020)中,RF算子参与融合模块以跨多分辨率特征图交换信息。下采样采用步长为2的跨步卷积,上采样采用双线性插值。重复 t 次跨步卷积,特征分辨率降低至 1 / 2 t 1/2^t 1/2t 。为了构建 M2MRF 变体,我们用 M2MRF 替换重复的跨步卷积和双线性插值。
论文提出了两种方式来用我们的 M2MRF 替换重复的 t 层跨步卷积。一种是用我们提出的 δ = 1/2 的 M2MRF 替换每个跨步卷积层,以逐步降低特征分辨率,将其称为cascade M2MRF。另一种是在M2MRF中直接将δ设置为 1 / 2 t 1/2^t 1/2t,以替换整个t层的strided卷积。我们将其称为one-step M2MRF。
同样,也有两种方式来替换比例因子为 2 t 2^t 2t的双线性插值层,一是δ=2的cascade M2MRF,逐步将特征分辨率提高到 2 t 2^t 2t。另一种是 δ = 2 t 2^t 2t 的one-step M2MRF,直接将特征分辨率提高到 2 t 2^t 2t。
以t = 2为例,图4分别示出了cascade M2MRF和one-step M2MRF分别用于下采样和上采样。

通过配备 M2MRF 的 HRNetV2 变体的高分辨率特征图,在其上附加多个二元分类器,以获得每个病变类别的概率图。考虑到微小病变分割中的极端类别不平衡,论文采用 Dice 损失(Milletari、Navab 和 Ahmadi 2016)来训练 M2MRF-HRNetV2 以及基线。
4. 实验和讨论
(1)为了验证 M2MRF 模块在微小病变分割上的有效性,两个公共数据集上进行了实验:
① DDR
② IDRiD。
(2)评估指标:
①精确率-召回率曲线下的面积(AUPR)
②mean F-score (mF)
③mean IoU (mIoU)
4.1. 实施细节
4.1.1. 数据集和增强
Ⅰ.数据集
- DDR共757张彩色眼底图像:
(1)尺寸范围:1088×1920~3456×5184;
(2)训练集:383张;
(3)验证集:149张;
(4)测试集:225张;
(5)专家将 24154、13035、1354 和 10563 个连通区域分别标注为 EX、HE、SE 和 MA。 - IDRiD共81张彩色眼底图像:
(1)尺寸:4288×2848;
(2)训练集:54张;
(3)测试集:27张;
(4)专家将 11716、1903、150 和 3505 个连通区域分别标注为 EX、HE、SE 和 MA。
Ⅱ.数据增强
-
图像预处理方法:
(1)DDR:对图像进行下采样:长边为1024,短边补0将其长度扩大到1024;
(2)IDRiD:图像大小调整为 1440 × 960。 -
数据增强方法:
①多尺度(0.5-2.0);
②旋转(90°、180°和270°);
③翻转(水平和垂直)。
4.1.2. 实验设置
M2MRF-HRNetV2 建立在 MMSegmentation (Contributors 2020) 提供的 HRNetV2 (Wang et al 2020) 实现之上。
我们使用高斯分布(零均值和标准差为 0.01)初始化与 M2MRF 和密集分类层(dense classification)相关的参数,其余参数使用 ImageNet 上的预训练模型(Krizhevsky、Sutskever 和 Hinton 2012)。
优化器:SGD。
超参数包括:
①初始学习率 (0.01 poly policy with power of 0.9)
②权重衰减 (0.0005)
③动量 (0.9)
④批量大小 (4)
⑤迭代周期(DDR 上为 60k,IDRiD 上为 40k)
下面只介绍有关IDRiD数据集相关的实验内容
4.2. IDRiD数据集上的结果
4.2.1. 与SOTA的RF上采样算子比较
为了验证论文提出的 M2MRF 的有效性,在 IDRiD (Porwal et al 2020) 上进行了实验,并与现有的八对 RF 算子进行了比较。表 5 报告了结果:

结果表明:
(1)M2MRF-C(即用于下采样的级联 M2MRF 和用于上采样的单步 M2MRF)在表中排名第一,而我们的 M2MRF-D(即用于下采样和上采样的级联 M2MRF)排名第二。
(2)M2MRF-C 在 mAUPR(67.24% vs. 65.01%)、mF(65.71% vs. 63.14%)和 mIoU(49.94% vs. 47.52%)方面持续大幅超过基线。
(3)还有一项有意思的结果:MaxPool/Bilinear interpolation 和 MaxPool/Unpooling这两对基于规则的RF算子比之前基于学习的RF算子取得更好的效果。可能的原因:基于学习的RF算子可能很难通过从感受野大小有限的小局部区域进行学习来保留微小病变引起的激活。
4.2.2. 与SOTA的分割方法的比较
论文将 M2MRF 与四种微小病变分割方法(VRT、PATech、iFLYTEK (Porwal et al 2020) 和 L-seg (Guo et al 2019))、六种最先进的基于 CNN 的方法和两种最新的基于Transformer的方法(Swinbase (Liu et al 2021b) 和 Twins-SVT-B (Chu et al 2021))进行比较。
在四种微小病变分割方法中:①L-Seg(Guo et al 2019)的性能直接借鉴了原始论文,其余的前三种方法借鉴了2018年ISBI大挑战。②六种基于 CNN 的分割方法和 Twins-SVT-B (Chu et al 2021) 的结果是通过使用 IDRiD (Porwal et al 2020) 在 ImageNet1K (Krizhevsky, Sutskever, and Hinton 2012) 上微调预训练获得的;Swin 基(Liu 等人2021b) 是 ImageNet-22K微调预训练获得的。
表 6 显示了比较结果,如下图所示:

从中我们得到以下观察结果:
(1)M2MRF 的四种变体在 mAUPR、mF 和 mIoU 方面始终优于所有表中的其他模型;
(2)M2MRF 的四种变体对指标 MA 分割有显着贡献,并且优于普通 HRNetV2(Wang 等人)2020)AUPR 提高了 4% 以上,F 分数提高了 5%,IoU 提高了 4%,这表明我们的 M2MRF 能够对微小病变保持更微妙的激活;
(3)四种变体中,M2MRF-C取得了最好的性能,在mAUPR、mF和mIoU上分别超过了最新的基于Transformer的分割方法 Swin-base(Liu et al 2021b)2.33%、1.67%和1.58%;
(4)专门为病灶分割设计的方法在 mAUPR 中比基于 CNN 的方法取得更好的效果(HRNetV2 除外)(Wang et al 2020);
(5)HRNetV2 (Wang et al 2020) 是微小病变分割任务的强大基线,并且在学习具有详细空间信息的高分辨率表示时,实现了与参与重大挑战的方法可竞争的 mAUPR。
我们还对最先进(SOTA)的方法进行了定性比较,并将其结果可视化在图 8 中:
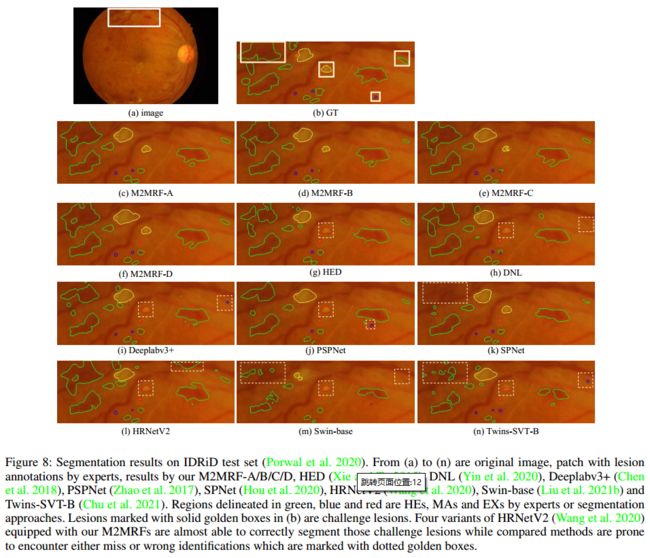
5. 结论
论文提出了一种名为 M2MRF 的简单 RF 算子,用于特征重组,它将特征下采样和上采样统一在一个框架中。我们的 M2MRF 考虑了长距离空间依赖性的贡献,并同时将大区域中的多个特征重组为多个目标特征。因此,它能够在特征重组过程中维持由微小病变引起的激活。它显示了两个公共微小病变分割数据集的显着改进,即 DDR和 IDRiD。此外,我们的 M2MRF 仅引入了额外的边际参数(marginal extra parameters),可用于替换现有 CNN 架构中的任意 RF 算子。