Pymoo：优化算法的性能指标(Performance Indicators)

• Github 仓库： Pymoo: 基于 Python 的多目标优化仓库 (MOO, Multi-objective Optimization)。
• Pymoo文档首页：Multi-objective Optimization in Python

✨ 注意：本文使用Pymoo版本为0.6.0。

一、Pymoo中提供的多目标优化算法的性能指标简介

对于单目标优化算法，由于每次优化运行都会产生一个最优解，因此算法的性能比较相当简单。然而，在多目标优化算法中，每次运行都会返回一组非支配解集（non-dominated set of solutions）。为了比较多组解的性能¹，Pymoo实现了以下常用的性能指标：

• 1、GD / IGD：给定一个Pareto前沿，这两个指标衡量了非支配集合(non-dominated set)与最优集(optimum)之间的偏差(deviation)。

  • （1）GD (Generational Distance)指标计算目标空间(objective space)中从非支配解集合中的每个解到Pareto前沿中距离自己最近解的平均欧几里德距离(Average Euclidean Distance)。该指标评价了非支配解集的收敛性，但是并没有对逼近Pareto前沿分散性(Diversity)的好坏。
  • （2）IGD(Inverted Generational Distance)指标计算目标空间(objective space)中从Pareto前沿中的每个解到非支配解集合中距离自己最近解的平均欧几里德距离(Average Euclidean Distance)。
  • 但是对于多目标优化问题的性能评价，不仅需要DG/IGD尽可能小，还需要非支配解集的解需要尽可能覆盖整个Pareto前沿，因此GD / IGD指标并不能全面的衡量多目标优化性能。

• 2、GD+ / IGD+²：GD与IGD指标的变体，在该指标中，欧几里德距离被一个考虑支配关系的距离度量所替代，并实现了与弱Pareto的相容性。

• 3、Hypervolume：目标空间的支配部分(dominated portion)可用于衡量非支配解的质量。Hypervolume指标越大表示解的性能越好。并且由于实际应用中我们并不能得到Pareto前沿，而该指标只需要提供参考点而不是Pareto前沿，这也是这个指标的一大优点。

二、Pymoo中优化算法的性能指标实现方法

算法的性能衡量是算法设计的基础。通常情况下在多目标优化场景中，我们无法计算得到真实的全局最优的距离，有时候甚至不知道最优解集，此时我们需要使用其他技术实现。但是，本文的重点在于入门Pymoo的优化算法性能指标代码实现方法，所以下面以一个Pareto前沿已知的情况。

首先定义一个zdt1问题，后面性能指标的实现都基于该问题：

import numpy as np
from pymoo.problems import get_problem
from pymoo.visualization.scatter import Scatter

# 得到zdt1问题的Pareto前沿
pf = get_problem("zdt1").pareto_front()

# 假设一个优化算法得到的非支配解集，从zdt1问题的Pareto前沿
# 中每隔10个抽一个，并乘以1.1
A = pf[::10] * 1.1

# 绘制结果
Scatter(legend=True).add(pf, label="Pareto Front").add(A, label="Non-Dominated Set Result").show()

代码执行结果如下图所示：

2.1 GD (Generational Distance)性能指标

GD性能指标测量多目标优化算法求得最优解集到Pareto前沿的距离³。假设优化算法得到的目标向量集合为$A=\{a_1,a_2,...,a_{|A|}\}$，参考点集合(reference points set)也成为Pareto 前沿为$Z=\{z_1,z_2,...,z_{|Z|}\}$，此时GD可以表示为：

$$\mathrm{GD}(A)=\frac{1}{|A|}(\sum _{i=1}^{|A|}{d}_i^p{)}^{1/p}$$
其中，$d_i$为$a_i$到参考点$Z$（Pareto前沿）中距离最近点的Euclidean距离。其结果表示目标向量集合$A$到Pareto前沿中最近点的平均距离。Pymoo的GD实现方法如下所示：

from pymoo.indicators.gd import GD

ind = GD(pf)
print("GD", ind(A))

代码执行结果如下图所示：

2.2 GD+ (Generational Distance Plus)性能指标

GD+的数学表达式如下所示：

$${\mathrm{GD}}^{+}(A)=\frac{1}{|A|}(\sum _{i=1}^{|A|}{d}_i^{{+}^2}{)}^{1/2}$$
其中，$d_i^{+}=max\{a_i-z_i,0\}$为对应于$z_i$的$a_i$到参考点$Z$（Pareto前沿）中距离最近点的修正距离，Pymoo的GD实现方法如下所示：

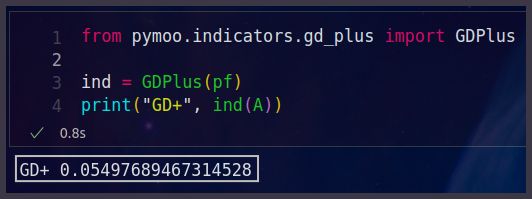
from pymoo.indicators.gd_plus import GDPlus

ind = GDPlus(pf)
print("GD+", ind(A))

代码执行结果如下图所示：

2.3 IGD(Inverted Generational Distance)性能指标

IGD性能指标表示GD的反向距离，即Pareto前沿$Z$中的点到目标向量集合$A$中距离最近点的GD距离，IGD的数学表达式如下所示：

$$\mathrm{IGD}(A)=\frac{1}{|Z|}(\sum _{i=1}^{|Z|}{{\hat{d}}_i}^p{)}^{1/p}$$
其中，${\hat{d}}_i$为$z_i$到目标向量集合$A$中距离最近点的Euclidean距离，Pymoo的IGD实现方法如下所示：

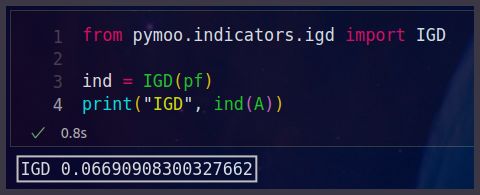
from pymoo.indicators.igd import IGD

ind = IGD(pf)
print("IGD", ind(A))

代码执行结果如下图所示：

2.4 IGD+ (Inverted Generational Distance Plus)性能指标

IGD+实现了IGD不具有的弱Pareto相容性，其数学表达式如下所示：

$${\mathrm{IGD}}^{+}(A)=\frac{1}{|Z|}(\sum _{i=1}^{|Z|}{d}_i^{{+}^2}{)}^{1/2}$$
其中，$d_i^{+}=max\{a_i-z_i,0\}$为对应于$z_i$的$a_i$到参考点$Z$（Pareto前沿）中距离最近点的修正距离，Pymoo的IGD+实现方法如下所示：

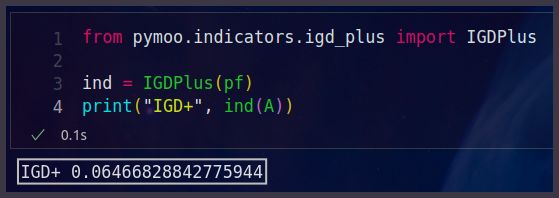
from pymoo.indicators.igd_plus import IGDPlus

ind = IGDPlus(pf)
print("IGD+", ind(A))

代码执行结果如下图所示：

2.5 Hypervolume性能指标

上面四种优化算法性能指标都是需要知道一个目标集。然而对于Hypervolume性能指标，我们只需要提供一个参考点即可。Pymoo是基于DEAP实现Hypervolume指标的。它通过计算面积/体积，这些面积/体积主要由参考点的一组解决定。

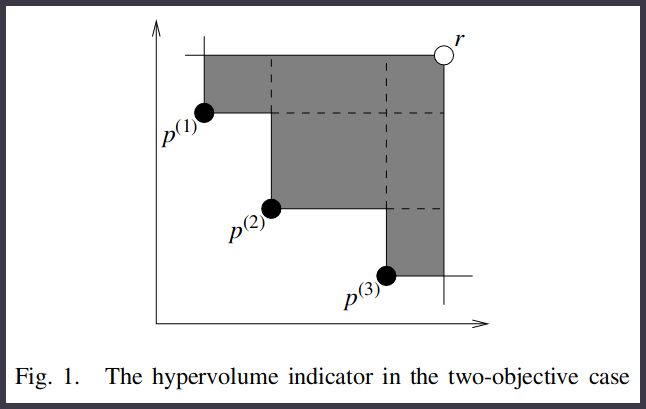
上图是来自于文献⁴，它展示了一个带有两个目标的例子，其中灰色面积表示被一个点集支配的区域。相比较于其他指标，目标是最小化Pareto前沿的距离，而这里我们希望最大化性能指标，Pymoo中实现Hypervolume性能指标的代码如下所示：

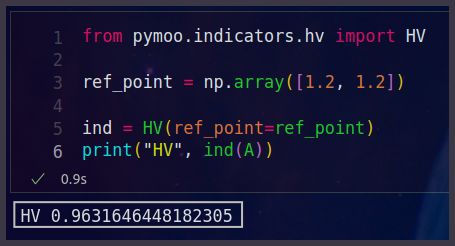
from pymoo.indicators.hv import HV

ref_point = np.array([1.2, 1.2])

ind = HV(ref_point=ref_point)
print("HV", ind(A))

参考文献

---

1. Quality Evaluation of Solution Sets in Multiobjective Optimisation: A Survey ↩︎

2. Modified Distance Calculation in Generational Distance and Inverted Generational Distance ↩︎

3. David A. Van Veldhuizen and David A. Van Veldhuizen. Multiobjective evolutionary algorithms: classifications, analyses, and new innovations. Technical Report, Evolutionary Computation, 1999. ↩︎

4. Carlos M. Fonseca, Luís Paquete, and Manuel López-Ibáñez. An improved dimension sweep algorithm for the hypervolume indicator. In Proceedings of the 2006 Congress on Evolutionary Computation (CEC 2006), pages 1157–1163. IEEE Press, Piscataway, NJ, July 2006. doi:10.1109/CEC.2006.1688440. ↩︎