-------------------2022.3.1更新----------------
感谢大家的厚爱,都一万多赞了,受宠若惊,帅地2023这一年也写了一个算法课程,发布在自己的网站(http://www.playoffer.cn)

如果你感兴趣,那么欢迎来看看哦:
拿下中大厂算法面试,14大算法专题 www.playoffer.cn/?p=1356
--------------------------------以下正文----------------------------
动态规划难吗?说实话,我觉得很难,特别是对于初学者来说,我当时入门动态规划的时候,是看 0-1 背包问题,当时真的是一脸懵逼。后来,我遇到动态规划的题,看的懂答案,但就是自己不会做,不知道怎么下手。就像做递归的题,看的懂答案,但下不了手,关于递归的,我之前也写过一篇套路的文章,如果对递归不大懂的,强烈建议看一看:为什么你学不会递归,告别递归,谈谈我的经验
对于动态规划,春招秋招时好多题都会用到动态规划,一气之下,再 leetcode 连续刷了几十道题
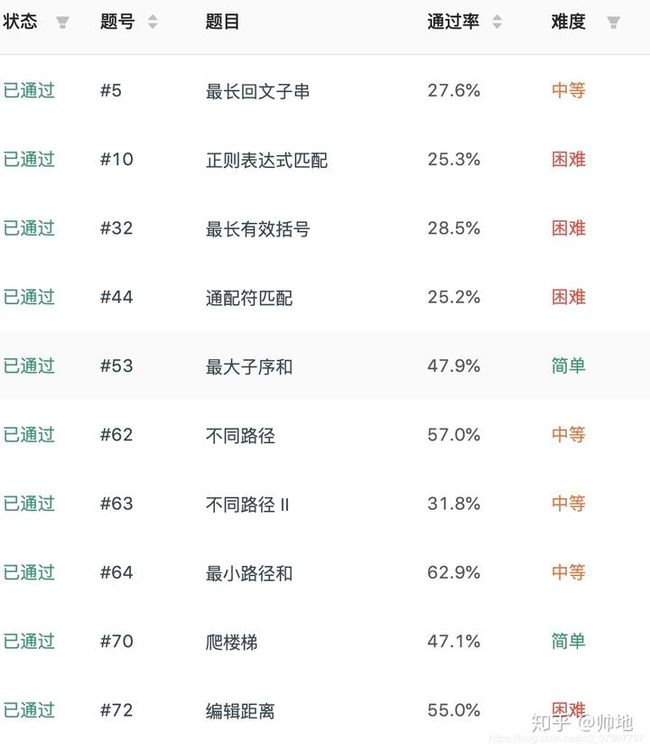
之后,豁然开朗 ,感觉动态规划也不是很难,今天,我就来跟大家讲一讲,我是怎么做动态规划的题的,以及从中学到的一些套路。相信你看完一定有所收获
如果你对动态规划感兴趣,或者你看的懂动态规划,但却不知道怎么下手,那么我建议你好好看以下,这篇文章的写法,和之前那篇讲递归的写法,是差不多一样的,将会举大量的例子。如果一次性看不完,建议收藏,同时别忘了素质三连。
为了兼顾初学者,我会从最简单的题讲起,后面会越来越难,最后面还会讲解,该如何优化。因为 80% 的动规都是可以进行优化的。不过我得说,如果你连动态规划是什么都没听过,可能这篇文章你也会压力山大。
一、动态规划的三大步骤
动态规划,无非就是利用历史记录,来避免我们的重复计算。而这些历史记录,我们得需要一些变量来保存,一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤,
如果你听不懂,也没关系,下面会有很多例题讲解,估计你就懂了。之所以不配合例题来讲这些步骤,也是为了怕你们脑袋乱了
第一步骤:定义数组元素的含义,上面说了,我们会用一个数组,来保存历史数组,假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点,就是规定你这个数组元素的含义,例如你的 dp[i] 是代表什么意思?
第二步骤:找出数组元素之间的关系式,我觉得动态规划,还是有一点类似于我们高中学习时的归纳法的,当我们要计算 dp[n] 时,是可以利用 dp[n-1],dp[n-2].....dp[1],来推出 dp[n] 的,也就是可以利用历史数据来推出新的元素值,所以我们要找出数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],这个就是他们的关系式了。而这一步,也是最难的一步,后面我会讲几种类型的题来说。
学过动态规划的可能都经常听到 最优子结构,把大的问题拆分成小的问题,说时候,最开始的时候,我是对 最优子结构一梦懵逼的。估计你们也听多了,所以这一次,我将 换一种形式来讲,不再是各种子问题,各种最优子结构。所以大佬可别喷我再乱讲,因为我说了,这是我自己平时做题的套路。
第三步骤:找出初始值。学过数学归纳法的都知道,虽然我们知道了数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],我们可以通过 dp[n-1] 和 dp[n-2] 来计算 dp[n],但是,我们得知道初始值啊,例如一直推下去的话,会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了,所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值,而这,就是所谓的初始值。
由了初始值,并且有了数组元素之间的关系式,那么我们就可以得到 dp[n] 的值了,而 dp[n] 的含义是由你来定义的,你想求什么,就定义它是什么,这样,这道题也就解出来了。
不懂?没事,我们来看三四道例题,我讲严格按这个步骤来给大家讲解。
二、案例详解
案例一、简单的一维 DP
问题描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
(1)、定义数组元素的含义
按我上面的步骤说的,首先我们来定义 dp[i] 的含义,我们的问题是要求青蛙跳上 n 级的台阶总共由多少种跳法,那我们就定义 dp[i] 的含义为:跳上一个 i 级的台阶总共有 dp[i] 种跳法。这样,如果我们能够算出 dp[n],不就是我们要求的答案吗?所以第一步定义完成。
(2)、找出数组元素间的关系式
我们的目的是要求 dp[n],动态规划的题,如你们经常听说的那样,就是把一个规模比较大的问题分成几个规模比较小的问题,然后由小的问题推导出大的问题。也就是说,dp[n] 的规模为 n,比它规模小的是 n-1, n-2, n-3.... 也就是说,dp[n] 一定会和 dp[n-1], dp[n-2]....存在某种关系的。我们要找出他们的关系。
那么问题来了,怎么找?
这个怎么找,是最核心最难的一个,我们必须回到问题本身来了,来寻找他们的关系式,dp[n] 究竟会等于什么呢?
对于这道题,由于情况可以选择跳一级,也可以选择跳两级,所以青蛙到达第 n 级的台阶有两种方式
一种是从第 n-1 级跳上来
一种是从第 n-2 级跳上来
由于我们是要算所有可能的跳法的,所以有 dp[n] = dp[n-1] + dp[n-2]。
(3)、找出初始条件
当 n = 1 时,dp[1] = dp[0] + dp[-1],而我们是数组是不允许下标为负数的,所以对于 dp[1],我们必须要直接给出它的数值,相当于初始值,显然,dp[1] = 1。一样,dp[0] = 0.(因为 0 个台阶,那肯定是 0 种跳法了)。于是得出初始值:
dp[0] = 0. dp[1] = 1. 即 n <= 1 时,dp[n] = n.
三个步骤都做出来了,那么我们就来写代码吧,代码会详细注释滴。
int f( int n ){
if(n <= 1)
return n;
// 先创建一个数组来保存历史数据
int[] dp = new int[n+1];
// 给出初始值
dp[0] = 0;
dp[1] = 1;
// 通过关系式来计算出 dp[n]
for(int i = 2; i <= n; i++){
dp[i] = dp[i-1] + dp[i-2];
}
// 把最终结果返回
return dp[n];
}
(4)、再说初始化
大家先想以下,你觉得,上面的代码有没有问题?
答是有问题的,还是错的,错在对初始值的寻找不够严谨,这也是我故意这样弄的,意在告诉你们,关于初始值的严谨性。例如对于上面的题,当 n = 2 时,dp[2] = dp[1] + dp[0] = 1。这显然是错误的,你可以模拟一下,应该是 dp[2] = 2。
也就是说,在寻找初始值的时候,一定要注意不要找漏了,dp[2] 也算是一个初始值,不能通过公式计算得出。有人可能会说,我想不到怎么办?这个很好办,多做几道题就可以了。
下面我再列举三道不同的例题,并且,再在未来的文章中,我也会持续按照这个步骤,给大家找几道有难度且类型不同的题。下面这几道例题,不会讲的特性详细哈。实际上 ,上面的一维数组是可以把空间优化成更小的,不过我们现在先不讲优化的事,下面的题也是,不讲优化版本。
案例二:二维数组的 DP
我做了几十道 DP 的算法题,可以说,80% 的题,都是要用二维数组的,所以下面的题主要以二维数组为主,当然有人可能会说,要用一维还是二维,我怎么知道?这个问题不大,接着往下看。
问题描述
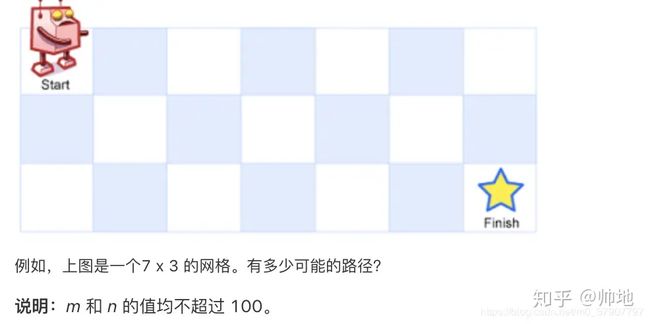
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?

这是 leetcode 的 62 号题: https://leetcode-cn.com/problems/unique-paths/
还是老样子,三个步骤来解决。
步骤一、定义数组元素的含义
由于我们的目的是从左上角到右下角一共有多少种路径,那我们就定义 dp[i] [j]的含义为:当机器人从左上角走到(i, j) 这个位置时,一共有 dp[i] [j] 种路径。那么,dp[m-1] [n-1] 就是我们要的答案了。
注意,这个网格相当于一个二维数组,数组是从下标为 0 开始算起的,所以 右下角的位置是 (m-1, n - 1),所以 dp[m-1] [n-1] 就是我们要找的答案。
步骤二:找出关系数组元素间的关系式
想象以下,机器人要怎么样才能到达 (i, j) 这个位置?由于机器人可以向下走或者向右走,所以有两种方式到达
一种是从 (i-1, j) 这个位置走一步到达
一种是从(i, j - 1) 这个位置走一步到达
因为是计算所有可能的步骤,所以是把所有可能走的路径都加起来,所以关系式是 dp[i] [j] = dp[i-1] [j] + dp[i] [j-1]。
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的,相当于计算机图中的最上面一行和左边一列。因此初始值如下:
dp[0] [0….n-1] = 1; // 相当于最上面一行,机器人只能一直往右走
dp[0…m-1] [0] = 1; // 相当于最左面一列,机器人只能一直往下走
撸代码
三个步骤都写出来了,直接看代码
public static int uniquePaths(int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
int[][] dp = new int[m][n]; //
// 初始化
for(int i = 0; i < m; i++){
dp[i][0] = 1;
}
for(int i = 0; i < n; i++){
dp[0][i] = 1;
}
// 推导出 dp[m-1][n-1]
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
O(n*m) 的空间复杂度可以优化成 O(min(n, m)) 的空间复杂度的,不过这里先不讲
案例三、二维数组 DP
写到这里,有点累了,,但还是得写下去,所以看的小伙伴,你们可得继续看呀。下面这道题也不难,比上面的难一丢丢,不过也是非常类似
问题描述
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
举例:
输入:
arr = [
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
和上面的差不多,不过是算最优路径和,这是 leetcode 的第64题:https://leetcode-cn.com/problems/minimum-path-sum/
还是老样子,可能有些人都看烦了,哈哈,但我还是要按照步骤来写,让那些不大懂的加深理解。有人可能觉得,这些题太简单了吧,别慌,小白先入门,这些属于 medium 级别的,后面在给几道 hard 级别的。
步骤一、定义数组元素的含义
由于我们的目的是从左上角到右下角,最小路径和是多少,那我们就定义 dp[i] [j]的含义为:当机器人从左上角走到(i, j) 这个位置时,最下的路径和是 dp[i] [j]。那么,dp[m-1] [n-1] 就是我们要的答案了。
注意,这个网格相当于一个二维数组,数组是从下标为 0 开始算起的,所以 由下角的位置是 (m-1, n - 1),所以 dp[m-1] [n-1] 就是我们要走的答案。
步骤二:找出关系数组元素间的关系式
想象以下,机器人要怎么样才能到达 (i, j) 这个位置?由于机器人可以向下走或者向右走,所以有两种方式到达
一种是从 (i-1, j) 这个位置走一步到达
一种是从(i, j - 1) 这个位置走一步到达
不过这次不是计算所有可能路径,而是计算哪一个路径和是最小的,那么我们要从这两种方式中,选择一种,使得dp[i] [j] 的值是最小的,显然有
dp[i] [j] = min(dp[i-1][j],dp[i][j-1]) + arr[i][j];// arr[i][j] 表示网格种的值
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n-1] 和所有的 dp[0….m-1] [0]。这个还是非常容易计算的,相当于计算机图中的最上面一行和左边一列。因此初始值如下:
dp[0] [j] = arr[0] [j] + dp[0] [j-1]; // 相当于最上面一行,机器人只能一直往左走
dp[i] [0] = arr[i] [0] + dp[i] [0]; // 相当于最左面一列,机器人只能一直往下走
代码如下
public static int uniquePaths(int[][] arr) {
int m = arr.length;
int n = arr[0].length;
if (m <= 0 || n <= 0) {
return 0;
}
int[][] dp = new int[m][n]; //
// 初始化
dp[0][0] = arr[0][0];
// 初始化最左边的列
for(int i = 1; i < m; i++){
dp[i][0] = dp[i-1][0] + arr[i][0];
}
// 初始化最上边的行
for(int i = 1; i < n; i++){
dp[0][i] = dp[0][i-1] + arr[0][i];
}
// 推导出 dp[m-1][n-1]
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + arr[i][j];
}
}
return dp[m-1][n-1];
}
O(n m) 的空间复杂度可以优化成 O(min(n, m)) 的空间复杂度的,不过这里先不讲
案例 4:编辑距离
这次给的这道题比上面的难一些,在 leetcdoe 的定位是 hard 级别。好像是 leetcode 的第 72 号题。
问题描述
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符 删除一个字符 替换一个字符
示例:
输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
解答
还是老样子,按照上面三个步骤来,并且我这里可以告诉你,90% 的字符串问题都可以用动态规划解决,并且90%是采用二维数组。
步骤一、定义数组元素的含义
由于我们的目的求将 word1 转换成 word2 所使用的最少操作数 。那我们就定义 dp[i] [j]的含义为:当字符串 word1 的长度为 i,字符串 word2 的长度为 j 时,将 word1 转化为 word2 所使用的最少操作次数为 dp[i] [j]。
有时候,数组的含义并不容易找,所以还是那句话,我给你们一个套路,剩下的还得看你们去领悟。
步骤二:找出关系数组元素间的关系式
接下来我们就要找 dp[i] [j] 元素之间的关系了,比起其他题,这道题相对比较难找一点,但是,不管多难找,大部分情况下,dp[i] [j] 和 dp[i-1] [j]、dp[i] [j-1]、dp[i-1] [j-1] 肯定存在某种关系。因为我们的目标就是,**从规模小的,通过一些操作,推导出规模大的。对于这道题,我们可以对 word1 进行三种操作
插入一个字符 删除一个字符 替换一个字符
由于我们是要让操作的次数最小,所以我们要寻找最佳操作。那么有如下关系式:
一、如果我们 word1[i] 与 word2 [j] 相等,这个时候不需要进行任何操作,显然有 dp[i] [j] = dp[i-1] [j-1]。(别忘了 dp[i] [j] 的含义哈)。
二、如果我们 word1[i] 与 word2 [j] 不相等,这个时候我们就必须进行调整,而调整的操作有 3 种,我们要选择一种。三种操作对应的关系试如下(注意字符串与字符的区别):
(1)、如果把字符 word1[i] 替换成与 word2[j] 相等,则有 dp[i] [j] = dp[i-1] [j-1] + 1;
(2)、如果在字符串 word1末尾插入一个与 word2[j] 相等的字符,则有 dp[i] [j] = dp[i] [j-1] + 1;
(3)、如果把字符 word1[i] 删除,则有 dp[i] [j] = dp[i-1] [j] + 1;
那么我们应该选择一种操作,使得 dp[i] [j] 的值最小,显然有
dp[i] [j] = min(dp[i-1] [j-1],dp[i] [j-1],dp[[i-1] [j]]) + 1;
于是,我们的关系式就推出来了,
步骤三、找出初始值
显然,当 dp[i] [j] 中,如果 i 或者 j 有一个为 0,那么还能使用关系式吗?答是不能的,因为这个时候把 i - 1 或者 j - 1,就变成负数了,数组就会出问题了,所以我们的初始值是计算出所有的 dp[0] [0….n] 和所有的 dp[0….m] [0]。这个还是非常容易计算的,因为当有一个字符串的长度为 0 时,转化为另外一个字符串,那就只能一直进行插入或者删除操作了。
代码如下
public int minDistance(String word1, String word2) {
int n1 = word1.length();
int n2 = word2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
// dp[0][0…n2]的初始值
for (int j = 1; j <= n2; j++)
dp[0][j] = dp[0][j - 1] + 1;
// dp[0…n1][0] 的初始值
for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
// 通过公式推出 dp[n1][n2]
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
// 如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
if (word1.charAt(i - 1) == word2.charAt(j - 1)){
p[i][j] = dp[i - 1][j - 1];
}else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
}
}
}
return dp[n1][n2];
}
最后说下,如果你要练习,可以去 leetcode,选择动态规划专题,然后连续刷几十道,保证你以后再也不怕动态规划了。当然,遇到很难的,咱还是得挂。
Leetcode 动态规划直达:https://leetcode-cn.com/tag/dynamic-programming/
三、如何优化?
前两天写一篇长达 8000 子的关于动态规划的文章告别动态规划,连刷40道动规算法题,我总结了动规的套路
这篇文章更多讲解我平时做题的套路,不过由于篇幅过长,举了 4 个案例之后,没有讲解优化,今天这篇文章就来讲解下,对动态规划的优化如何下手,并且以前几天那篇文章的题作为例子直接讲优化,如果没看过的建议看一下(不看也行,我会直接给出题目以及没有优化前的代码):告别动态规划,连刷40道动规算法题,我总结了动规的套路
四、优化核心:画图!画图!画图
没错,80% 的动态规划题都可以画图,其中 80% 的题都可以通过画图一下子知道怎么优化,当然,DP 也有一些很难的题,想优化可没那么容易,不过,今天我要讲的,是属于不怎么难,且最常见,面试笔试最经常考的难度的题。
下面我们直接通过三道题目来讲解优化,你会发现,这些题,优化过后,代码只有细微的改变,你只要会一两道,可以说是会了 80% 的题。
O(nm) 空间复杂度优化成 O(n)
上次那个青蛙跳台阶的 dp 题是可以把空间复杂度 O( n) 优化成 O(1),本来打算从这道题讲起的,但想了下,想要学习 dp 优化的感觉至少都是 小小大佬了,所以就不讲了,就从二维数组的 dp 讲起。
案例1:最多路径数
问题描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?

这是 leetcode 的 62 号题: https://leetcode-cn.com/problems/unique-paths/
这道题的 dp 转移公式是 dp[i] [j] = dp[i-1] [j] + dp[i] [j-1],代码如下
不懂的看我之前文章: 告别动态规划,连刷40道动规算法题,我总结了动规的套路
public static int uniquePaths(int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
int[][] dp = new int[m][n]; //
// 初始化
for(int i = 0; i < m; i++){
dp[i][0] = 1;
}
for(int i = 0; i < n; i++){
dp[0][i] = 1;
}
// 推导出 dp[m-1][n-1]
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
这种做法的空间复杂度是 O(n * m),下面我们来讲解如何优化成 O(n)。
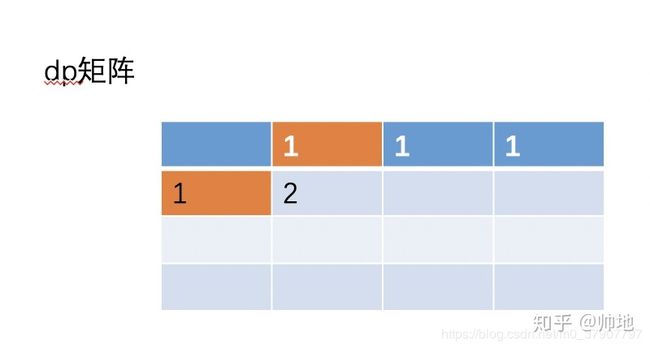
dp[i] [j] 是一个二维矩阵,我们来画个二维矩阵的图,对矩阵进行初始化
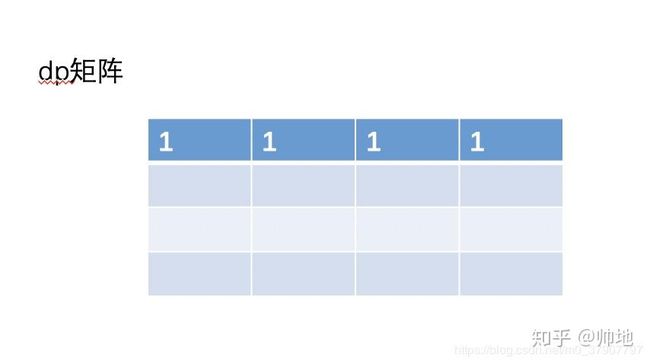
然后根据公式 dp[i][j] = dp[i-1][j] + dp[i][j-1] 来填充矩阵的其他值。下面我们先填充第二行的值。

大家想一个问题,当我们要填充第三行的值的时候,我们需要用到第一行的值吗?答是不需要的,不行你试试,当你要填充第三,第四…第 n 行的时候,第一行的值永远不会用到,只要填充第二行的值时会用到。
根据公式 dp[i][j] = dp[i-1][j] + dp[i][j-1],我们可以知道,当我们要计算第 i 行的值时,除了会用到第 i - 1 行外,其他第 1 至 第 i-2 行的值我们都是不需要用到的,也就是说,对于那部分用不到的值我们还有必要保存他们吗?
答是没必要,我们只需要用一个一维的 dp[] 来保存一行的历史记录就可以了。然后在计算机的过程中,不断着更新 dp[] 的值。单说估计你可能不好理解,下面我就手把手来演示下这个过程。
1、刚开始初始化第一行,此时 dp[0…n-1] 的值就是第一行的值。

2、接着我们来一边填充第二行的值一边更新 dp[i] 的值,一边把第一行的值抛弃掉。
为了方便描述,下面我们用arr (i,j)表示矩阵中第 i 行 第 j 列的值。从 0 开始哈,就是说有第 0 行。
(1)、显然,矩阵(1, 0) 的值相当于以往的初始化值,为 1。然后这个时候矩阵 (0,0)的值不在需要保存了,因为再也用不到了。

这个时候,我们也要跟着更新 dp[0] 的值了,刚开始 dp[0] = (0, 0),现在更新为 dp[0] = (1, 0)。
(2)、接着继续更新 (1, 1) 的值,根据之前的公式 (i, j) = (i-1, j) + (i, j- 1)。即 (1,1)=(0,1)+(1,0)=2。
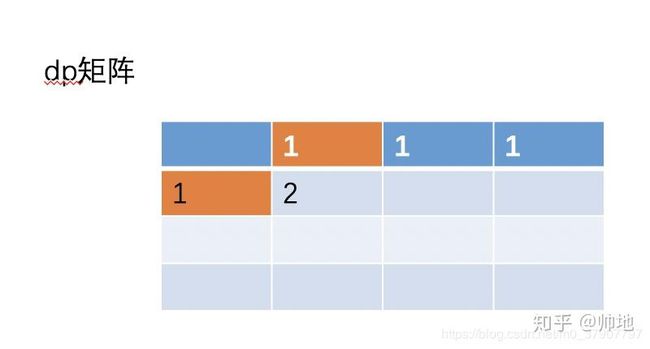
大家看图,以往的二维的时候, dp[i][j] = dp[i-1] [j]+ dp[i][j-1]。现在转化成一维,不就是 dp[i] = dp[i] + dp[i-1] 吗?
即 dp[1] = dp[1] + dp[0],而且还动态帮我们更新了 dp[1] 的值。因为刚开始 dp[i] 的保存第一行的值的,现在更新为保存第二行的值。

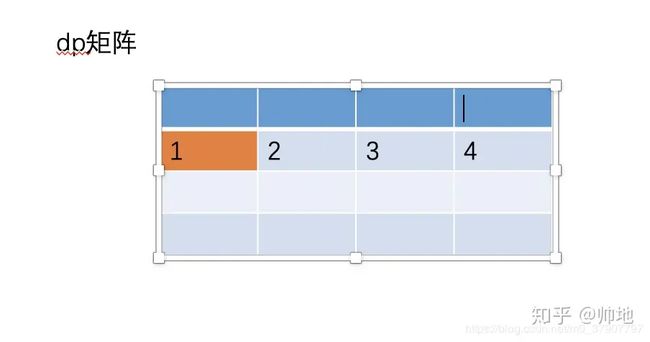
(3)、同样的道理,按照这样的模式一直来计算第二行的值,顺便把第一行的值抛弃掉,结果如下
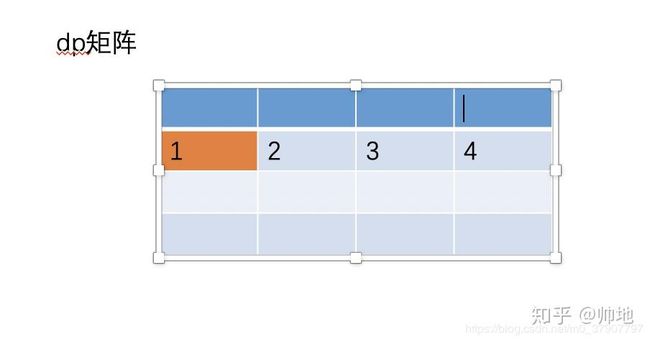
此时,dp[i] 将完全保存着第二行的值,并且我们可以推导出公式
dp[i] = dp[i-1] + dp[i]
dp[i-1] 相当于之前的 dp[i-1][j],dp[i] 相当于之前的 dp[i][j-1]。
于是按照这个公式不停着填充到最后一行,结果如下:

最后 dp[n-1] 就是我们要求的结果了。所以优化之后,代码如下:
public static int uniquePaths(int m, int n) {
if (m <= 0 || n <= 0) {
return 0;
}
int[] dp = new int[n]; //
// 初始化
for(int i = 0; i < n; i++){
dp[i] = 1;
}
// 公式:dp[i] = dp[i-1] + dp[i]
for (int i = 1; i < m; i++) {
// 第 i 行第 0 列的初始值
dp[0] = 1;
for (int j = 1; j < n; j++) {
dp[j] = dp[j-1] + dp[j];
}
}
return dp[n-1];
}
案例2:编辑距离
接着我们来看昨天的另外一道题,就是编辑矩阵,这道题的优化和这一道有一点点的不同,上面这道 dp[i][j] 依赖于 dp[i-1][j] 和 dp[i][j-1]。而还有一种情况就是 dp[i][j] 依赖于 dp[i-1][j],dp[i-1][j-1] 和 dp[i][j-1]。
问题描述
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符 删除一个字符 替换一个字符
示例:
输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
解答
昨天的代码如下所示,不懂的记得看之前的文章哈:告别动态规划,连刷40道动规算法题,我总结了动规的套路
public int minDistance(String word1, String word2) {
int n1 = word1.length();
int n2 = word2.length();
int[][] dp = new int[n1 + 1][n2 + 1];
// dp[0][0…n2]的初始值
for (int j = 1; j <= n2; j++)
dp[0][j] = dp[0][j - 1] + 1;
// dp[0…n1][0] 的初始值
for (int i = 1; i <= n1; i++) dp[i][0] = dp[i - 1][0] + 1;
// 通过公式推出 dp[n1][n2]
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
// 如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
if (word1.charAt(i - 1) word2.charAt(j - 1)){
p[i][j] = dp[i - 1][j - 1];
}else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
}
}
}
return dp[n1][n2];
}
没有优化之间的空间复杂度为 O(n*m)
大家可以自己动手做下,按照上面的那个模式,你会优化吗?

对于这道题其实也是一样的,如果要计算 第 i 行的值,我们最多只依赖第 i-1 行的值,不需要用到第 i-2 行及其以前的值,所以一样可以采用一维 dp 来处理的。
不过这个时候要注意,在上面的例子中,我们每次更新完 (i, j) 的值之后,就会把 (i, j-1) 的值抛弃,也就是说之前是一边更新 dp[i] 的值,一边把 dp[i] 的旧值抛弃的,不过在这道题中则不可以,因为我们还需要用到它。
哎呀,直接举例子看图吧,文字绕来绕去估计会绕晕你们。当我们要计算图中 (i,j) 的值的时候,在案例1 中,我们值需要用到 (i-1, j) 和 (i, j-1)。(看图中方格的颜色)

不过这道题中,我们还需要用到 (i-1, j-1) 这个值(但是这个值在以往的案例1 中,它会被抛弃掉)

所以呢,对于这道题,我们还需要一个额外的变量 pre 来时刻保存 (i-1,j-1) 的值。推导公式就可以从二维的
dp[i][j] = min(dp[i-1][j] , dp[i-1][j-1] , dp[i][j-1]) + 1
转化为一维的
dp[i] = min(dp[i-1], pre, dp[i]) + 1。
所以呢,案例2 其实和案例1 差别不大,就是多了个变量来临时保存。最终代码如下(但是初学者话,代码也没那么好写)
代码如下
public int minDistance(String word1, String word2) {
int n1 = word1.length();
int n2 = word2.length();
int[] dp = new int[n2 + 1];
// dp[0…n2]的初始值
for (int j = 0; j <= n2; j++)
dp[j] = j;
// dp[j] = min(dp[j-1], pre, dp[j]) + 1
for (int i = 1; i <= n1; i++) {
int temp = dp[0];
// 相当于初始化
dp[0] = i;
for (int j = 1; j <= n2; j++) {
// pre 相当于之前的 dp[i-1][j-1]
int pre = temp;
temp = dp[j];
// 如果 word1[i] 与 word2[j] 相等。第 i 个字符对应下标是 i-1
if (word1.charAt(i - 1) word2.charAt(j - 1)){
dp[j] = pre;
}else {
dp[j] = Math.min(Math.min(dp[j - 1], pre), dp[j]) + 1;
}
// 保存要被抛弃的值
}
}
return dp[n2];
}
总结
上面的这些题,基本都是不怎么难的入门题,除了最后一道相对难一点。并且基本 80% 的二维矩阵 dp 都可以像上面的方法一样优化成 一维矩阵的 dp,核心就是要画图,看他们的值依赖,当然,还有很多其他比较难的优化,但是,我遇到的题中,大部分都是我上面这种类型的优化。后面如何遇到其他的,我会作为案例来讲,今天就先讲最普遍最通用的优化方案。记住,画二维 dp 的矩阵图,然后看元素之间的值依赖,然后就可以很清晰着知道该如何优化了。
在之后的文章中,我也会按照这个步骤,在给大家讲四五道动态规划 hard 级别的题,会放在每天推文的第二条给大家学习。如果觉得有收获,不放三连走起来(点赞、感谢、分享),嘻嘻。
--------------------2023.5.14更新-------------
帅地2023这一年也写了一个算法课程:
拿下中大厂算法面试,14大算法专题 www.playoffer.cn/?p=1356
部分目录:
1. 第一章:如何准备一场算法面试?
2. 第二章:时间复杂度分析
3. 第三章:二分查找基础
4. LeetCode704.二分查找 简单
5. LeetCode69.x的平方根. 简单
6. LeetCode27.移除元素 简单
7. LeetCode11.盛最多水的容器 中等
8. LeetCode209. 长度最小的子数组 中等
9. 巧用数组下标法
10. 递归入门与优化 + 例题
11. 第四章:理解链表
12. LeetCode203.移除链表元素 简单
13. LeetCode876. 链表的中间结点 简单
14. 剑指 Offer 22. 链表中倒数第k个节点 中等
15. LeetCode19. 删除链表的倒数第 N 个结点 中等
16. 剑指 Offer 06. 从尾到头打印链表 简单
17. LeetCode160. 相交链表 简单
18. LeetCode206. 反转链表 简单
19. LeetCode92. 反转链表 II 中等
20. LeetCode25. K 个一组翻转链表 困难
21. LeetCode141. 环形链表 简单
22. Leectode142. 环形链表 II 中等
23. LeetCode21. 合并两个有序链表 简单
24. LeetCode61. 旋转链表 中等
25. LeetCode148. 排序链表 中等
26. LeetCode382. 链表随机节点 中等
27. LeetCode138. 复制带随机指针的链表 中等
28. LeetCode146. LRU 缓存 中等
29. 队列和栈的一些说明
30. LeetCode232. 用栈实现队列 简单
31. LeetCode225. 用队列实现栈 简单
32. LeetCode20. 有效的括号 简单
33. LeetCode150. 逆波兰表达式求值 中等
34. LeetCode155. 最小栈 中等
35. 优先队列基础讲解
36. LeetCode215. 数组中的第K个最大元素 中等
37. LeetCode347. 前 K 个高频元素 中等
38. LeetCode295. 数据流的中位数 困难
39. 单调栈科普与例题
40. LeetCode1475. 商品折扣后的最终价格 简单
41. LeetCode239. 滑动窗口最大值 困难
42. 二叉树考点分析
43. 二叉树前序中序后序遍历(递归版本)
44. LeetCode144. 二叉树的前序遍历 简单
45. LeetCode94. 二叉树的中序遍历 简单
46. 二叉树的后序遍历 简单
47. 二叉树层序遍历(基本版) 中等
48. 二叉树的层序遍历(进阶版) 中等
49. 二叉树的最大深度 简单
50. 平衡二叉树 简单
51. 二叉树的镜像 简单
52. 对称二叉树 简单
53. 二叉树的右视图 中等
54. 二叉树最大宽度 中等
55. 从前序与中序遍历序列构造二叉树 中等
56. 从中序与后序遍历序列构造二叉树 中等
57. 二叉搜索树中第K小的元素 中等
58. 序列化二叉树 困难
59. 路径总和1 简单
60. 路径总和2 中等
61. 二叉搜索树的最近公共祖先 中等
62. 二叉树的最近公共祖先 中等
编辑于 2023-06-03 21:55 ・IP 属地广东
赞同 1.3 万 524 条评论
喜欢 收藏 申请转载
文章被以下专栏收录
-
帅地玩编程
一大波原创算法+计算机基础文章即将来袭
LeetCode-JS
复习算法、数据结构为主。有兴趣的可以进群。
































牛逼
这种好东西一般只会在收藏夹吃灰
好哥哥,链接又没了
原题要求“只能向下或者向右”,所以不可能遍历或者返回某处。路径长度都是一样的,是不过是在哪里转弯的问题。
第一个爬楼梯,代码有问题,定义初始值应该是dp[1]=1,dp[2]=2
当然,遇到很难的,咱还是得挂。
那个leetcode困难题有个dp少了’d’
dp[i] = dp[i-1] + dp[i]
dp[i-1] 相当于之前的 dp[i-1][j],dp[i] 相当于之前的 dp[i][j-1]。这里是不是写反了,我感觉是:dp[i-1] 相当于之前的 dp[i][j-1],dp[i] 相当于之前的 dp[i-1][j]