详解C++区间题之线段树（动态开点）框架代码(附加一个有趣的差分有序集合方法)

前言–解决区间问题的各类方法总结！

数组不变，区间查询：前缀和、树状数组、线段树；
数组单点修改，区间查询：树状数组、线段树；
数组区间修改，单点查询：差分数组、线段树；
数组区间修改，区间查询：线段树；

一、线段树的介绍

线段树解决的是「区间和」的问题，且该「区间」会被修改（注意，必须是区间加法，才能将大问题化成小问题）。通常，对于需要多次求某一个区间的和，首先会想到利用「前缀和」，但若区间内的值会被修改，那么利用前缀和就没有那么高效了，因为每一次更新，前缀和数组必须也随之更新。因此需要引入线段树（这里区间和指的是：对于区间【L,R】的答案，可以由【L，M】和【M+1，R】来求出）

二、线段树的实现

由于线段树需要解决的是两个问题，因此实现方法也是两个「求区间和」&&「修改区间」，且时间复杂度均为 O(logn)，其核心是线段树的每个节点代表一个区间，例如：nums = [1, 2, 3, 4, 5]

PS:图中各个节点的值就是该区间的和 (其实还可以根据题目问题，改变表示的含义！！)而根节点代表的区间是问题的总区间，如这个例子，问题的总区间就是数组的长度 [0, 4]。

1 线段树的建立（仅适用于给定具体区间范围的）

从上图其实也可以感觉出来，线段树其实是一棵近似的完全二叉树，因此我们可以用一个数组来表示线段树，而根据完全二叉树的性质：假设根节点为i，那么左孩子为2*i，右孩子为2*i+1

void build(int root,int start,int end){
//这个start和end是根据题目中给定的具体区间范围
    if(start == end){
        tree[root] = num[start];
        return;
    }
    int leftroot = root * 2;//左结点
    int rightroot = root * 2 + 1;//右结点
    int mid = (start+end)/2;
    build(leftroot,start,mid);//递归计算左结点
    build(rightroot,mid+1,end);//递归计算右结点
    tree[root] = tree[leftroot] + tree[rightroot];// **核心计算公式**
    //本题是根结点值=左根（左区间的和）+右根(右区间的和)
}

2 线段树的动态开点

但是很多时候，题目中都没有给出很具体的范围，只有数据的取值范围，一般都很大，所以我们更常用的是「动态开点」，而动态开点正是在更新或查询地时候动态建立的：

2.1 线段树的数据结构

由1中的递归建立可知，其由三个属性，然而想要动态开点，还需要一个额外的属性：「懒惰标记」。这也是实现线段树的插入和查询都是logn 的关键，lazy标记将此区间标记，表示这个区间的值已经更新，但是子区间却没更新，更新的信息就是lazy里存的值。

struct Node {
      int val,lazy;//当前节点值和懒惰标记
      Node *left;
      Node *right;
      Node() : val(0), lazy(0), left(nullptr), right(nullptr) {}

2.2 线段树的查询

在区间 [start, end] 中查询区间 [l, r] 的结果，即 [l ,r] 保持不变
例如我想查询总区间0-4内的2和4，应该这样调用该函数：query(root, 0, 4, 2, 4)
【步骤】其实和更新步骤的思想差不多
1、当我们需要修改下第i个数据(区间[l,r])时，就要从根节点向下深搜。
2.a、如果要修改的区间完全覆盖当前区间，就直接返回这个区间的值
2.b、如果没有完全覆盖，则先下传lazy标记到子区间，
3.1.b、如果修改区间跟左儿子有交集，那么搜索左儿子(递归)
3.2.b、如果修改区间跟右儿子有交集，那么搜索右儿子(递归)
4.b、最后合并处理两边查询的数据

int query(TreeNode* root, int start, int end, int l, int r) {
    // 区间 [l ,r] 完全包含于区间 [start, end]
    // 例如：[2, 4] = [2, 2] + [3, 4]，当 [start, end] = [2, 2] 或者 [start, end] = [3, 4]，直接返回
    if (l <= start && end <= r) return root->val;
    // 把当前区间 [start, end] 均分得到左右孩子的区间范围：因此
    // root 左孩子区间 [start, mid]
    // root 右孩子区间 [mid + 1, end]
    int ans = 0;
    int mid = start+(end - start)/2;
    // 下推标记
    pushDown(root, mid - start + 1, end - mid);//注意这里的+1
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (l <= mid) ans += query(root->left, start, mid, l, r);
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (r > mid) ans += query(root->right, mid + 1, end, l, r);
    // ans 把左右子树的结果都累加起来了，与树的后序遍历同理
    return ans;
}

下推懒惰标记的函数
注意由于时动态开点，因此在下推懒惰标记的时候，如果节点不存在左右孩子节点，那么我们就创建左右孩子节点。
lazy标记的精髓就是延时处理
【输入量：root，左子树节点数以及右子树节点数】
【下推步骤】
1、首先，先动态开点，查询是否左右有自节点，没有直接开点即可。
2、其次就是看看有无lazy，如果没有，那根本没必要下推了，直接退出！
3、更新左右节点的值
4、将标记下推给孩子节点
5、取消当前节点标记

//下推懒惰标记
void pushdown(Node* root, int leftNum, int rightNum) {//下放懒标记
	// 动态开点
    if (root->left == nullptr) root->left = new TreeNode();
    if (root->right == nullptr) root->right = new TreeNode();
    // 如果 lazy 为 0，表示没有标记
    if (root->lazy == 0) return ;
    // 当前节点加上标记值
    // 注意：需要加上该子树所有叶子节点
    root->left->val += root->lazy * leftNum;
    root->right->val += root->lazy * rightNum;
    // 把标记下推给孩子节点
    root>left->lazy = root->lazy;
   	root->right->lazy = root->lazy;
    // 取消当前节点标记
    root->lazy = 0;
}

2.3 线段树的更新

这个由两个部分组成，分别为上下推懒惰标记和更新两个函数。
更新的函数
1、当我们需要修改下第i个数据(区间[l,r])时，就要从根节点向下深搜。
2.a、如果要修改的区间完全覆盖当前区间，就直接修改这个区间，并打上lazy标记。
2.b、如果没有完全覆盖，则先下传lazy标记到子区间，再清除当前区间的lazy标记（下面的pishdown函数）。
3.1.b、如果修改区间跟左儿子有交集，那么搜索左儿子(递归)
3.2.b、如果修改区间跟右儿子有交集，那么搜索右儿子(递归)
4.b、最后将当前区间的值更新（第四部分上推）

void update(Node* root, int start, int end, int l, int r, int val) {
    // 找到满足要求的区间
    if (l <= start && end <= r) {
        // 区间节点加上更新值
        // 注意：需要加上该子树所有叶子节点（由于求和嘛，所以区间都要+个val）
        root->val += (end - start + 1) * val;
        // 添加懒惰标记
        root->add += val;
        return ;
    }
    int mid = start+(end - start)/2;
    // 下推标记
    pushDown(root, mid - start + 1, end - mid);
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (l <= mid) update(root->left, start, mid, l, r, val);
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (r > mid) update(root->right, mid + 1, end, l, r, val);
    // 将当前区间的值更新
     pushUp(root);
}

2.4线段树的上推函数

即更新最后一步，这一步其实很简单，但是对于线段树中不同的内容是不一样的。首先是最常见的节点为区间和：

void pushUp(Node* root)
{
	root->val = root->left->val+root->right->val;
}

像前几个博客中699掉落的方块中，就是节点存区间内的最大值，而不是区间和的值。

void pushUp(Node* root)
{
	root->val = max(root->left->val, root->right->val);
}

三、线段树的应用

下面让我们用模板轻松秒杀三困难并加强对模板的理解

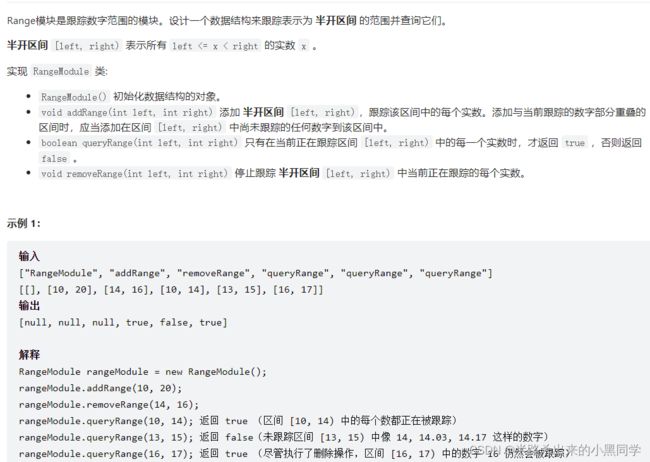
1 第一个题—715. Range 模块

题目

完整代码

class RangeModule {
public:
    RangeModule() {
    }
    void addRange(int left, int right) {
        update(root,1,N,left,right-1,1);//不用改模板，这里就能改变其左开右闭的环境了！
    }
    
    bool queryRange(int left, int right) {
        return query(root,1,N,left,right-1);
    }
    void removeRange(int left, int right) {
        update(root,1,N,left,right-1,-1);
    }
    // 上面是官方的框架，下面是套用的模板
    struct Node{
        bool val;//注意这里不是普通值了，而是布尔的是与否
        int lazy;
        Node* left;
        Node* right;
        Node(): val(false),lazy(0),left(nullptr),right(nullptr){}
    };
    int N = 1e9-1;
    Node* root = new Node();
    bool query(Node*root,int start,int end,int left,int right)
    {
        if(left<=start && right>=end) return root->val;
        int mid = (start + end) >> 1;
        PushDown(root,mid-start+1,end-mid);
        //查询所有子树是否全被覆盖
        bool ans = true;
        if(left<=mid) ans = (ans && query(root->left,start,mid,left,right));
        if(!ans) return ans;//此处加了个优化
        if(right>mid) ans = (ans && query(root->right,mid+1,end,left,right));
        return ans;
    }
    void update(Node* root,int start,int end,int left,int right,int val)
    {
        if(left<=start && right>=end)
        {
            //记住，凡是修改bool，就要==1判断一下子，否则还是会以为是数值！！
            root->val = val == 1?true:false;
            root->lazy = val;
            return;
        }
        int mid = (start + end) >> 1;
        PushDown(root,mid-start+1,end-mid);
        if(left<=mid) update(root->left,start,mid,left,right,val);
        if(right>mid) update(root->right,mid+1,end,left,right,val);
        root->val = root->left->val && root->right->val;
    }
    void PushDown(Node* root ,int leftnum, int rightnum)
    {
        if(root->left==nullptr) root->left = new Node();
        if(root->right==nullptr) root->right = new Node();
        if(root->lazy == 0) return;
        root->left->val = root->lazy==1?true:false;
        root->right->val = root->lazy==1?true:false;
        root->left->lazy = root->lazy;
        root->right->lazy = root->lazy;
        root->lazy = 0;
    }
};

糟糕的C++中new操作

上述的模板如果没有query那里的优化一步，直接cv提交，发现会TLE。难道是线段树不适用于本题吗？其实不然，而是由于c++中的new操作实在是太耗费时间了。因为new分配的内存是在堆区的，而堆区分配内存效率不是很高，涉及到用一定的算法在堆内存中搜索足够用的空间，如果没有满足条件的空间，会合并内存碎片，合并后的内存满足申请要求了才会返回，否则new失败。所以C++中用指针动态开点的方式会造成很大的时间消耗。

template<class T> class CachedObj{
public:
	void *operator new(size_t s){
		if (!head){
			T *a=new T[SIZE];
			for (size_t i=0;i<SIZE;++i)add(a+i);
		}
		T *p=head;head=head->CachedObj<T>::next;return p;
	}
	void operator delete(void *p,size_t){if (p)add(static_cast<T*>(p));}
	virtual ~CachedObj(){}
protected:
	T *next;
private:
	static T *head;static const size_t SIZE;
	static void add(T *p){p->CachedObj<T>::next=head;head=p;}
};
template<class T> T *CachedObj<T>::head=0;
template<class T> const size_t CachedObj<T>::SIZE=10000;
struct Node:public CachedObj<Node>{
        bool val;
        int lazy;
        Node* left;
        Node* right;
        Node(): val(false),lazy(0),left(nullptr),right(nullptr){}
    };

而这个它以 10000 个 Node 为一组(数目可自行调整)一次性分配内存，这是比一个个分配 10000 个 Node 要快的。这一组 Node 用完后自动分配下一组，保证内存动态增长且不浪费太多。另外继承这个 CachedObj 之后，对 Node 的 new 操作就自动变成了 CachedObj 中的 new 操作，非常省事。
但是每次刷题都定义新的new也太烦人了，因此我们可以采用还是动态开点，但是提前申请好内存数，也就是M，这个M是可以试出来。WA了不够再添，直到所有测试用例过了！

class RangeModule {
public:
    RangeModule() {
    }
    void addRange(int left, int right) {
        update(0,1,N,left,right-1,1);//注意，这里成0了！
    }
    
    bool queryRange(int left, int right) {
        return quary(0,1,N,left,right-1);
    }
    void removeRange(int left, int right) {
        update(0,1,N,left,right-1,-1);
    }
    struct Node{
    int left;
    int right;
    int lazy;
    bool val;
    Node(): val(false),lazy(0),left(0),right(0){}//这里左右直接初始为0就行
};
    constexpr static int N = 1e9;
    constexpr static int M = 500000;//这里就是提前申请的内存数，如果WA了，此处就可以在修改
    Node tree[M];
    int idx = 0;//这个就是配合动态开点的关键，通过它和pushdown第一个函数的配合来开点
    bool quary(int index ,int start,int end,int left,int right)
    {
        if(left<=start && right>=end) return tree[index].val;
        int mid = (start + end) >> 1;
        PushDown(index,mid-start+1,end-mid);
        //查询所有子树是否全被覆盖
        bool ans = true;
        if(left<=mid) ans = (ans && quary(tree[index].left,start,mid,left,right));
        if(right>mid) ans = (ans && quary(tree[index].right,mid+1,end,left,right));
        return ans;
    }
    void update(int index,int start,int end,int left,int right,int val)
    {
        if(left<=start && right>=end)
        {
            //记住，凡是修改bool，就要==1判断一下子，否则还是会以为是数值！！
            tree[index].val = val == 1;
            tree[index].lazy = val;
            return;
        }
        int mid = (start + end) >> 1;
        PushDown(index,mid-start+1,end-mid);
        if(left<=mid) update(tree[index].left,start,mid,left,right,val);
        if(right>mid) update(tree[index].right,mid+1,end,left,right,val);
        tree[index].val = tree[tree[index].left].val && tree[tree[index].right].val;
    }
    void PushDown(int index ,int leftnum, int rightnum)
    {
        if(tree[index].left==0) tree[index].left = ++idx;
        if(tree[index].right==0) tree[index].right = ++idx;
        if(tree[index].lazy == 0) return;
         tree[tree[index].left].val = tree[index].lazy==1;
        tree[tree[index].right].val = tree[index].lazy==1;
         tree[tree[index].left].lazy = tree[index].lazy;
        tree[tree[index].right].lazy = tree[index].lazy;
        tree[index].lazy = 0;
    }
};

2 第二个题—699.掉落的方块（节点的值存放最大值的情形1）

题目

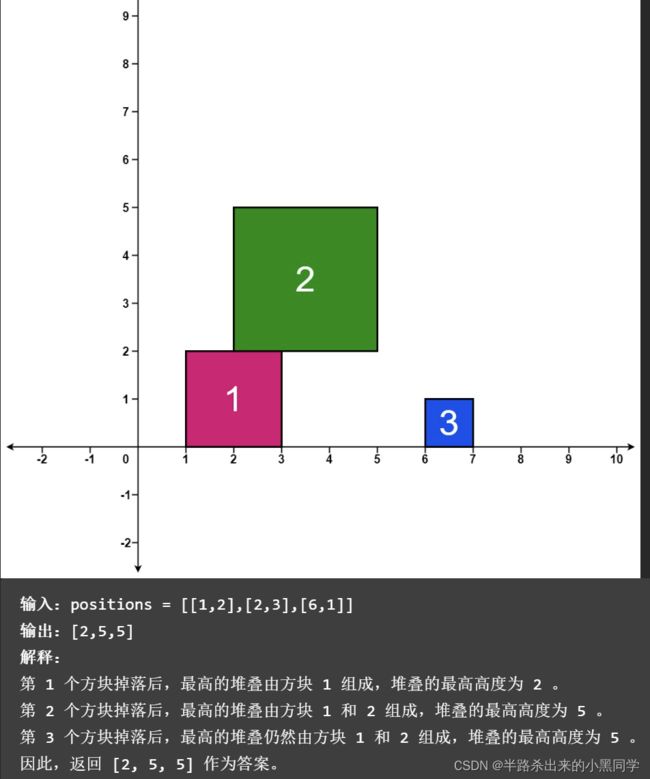
本题为什么节点的值不可以是区间和了呢，因为查询最高高度，其实区间和也可以，就是返回一个根节点的节点值，但那样查询起来复杂度就高了，因此不如直接存放最大值，这样返回的时候直接查看根节点就行了！
【注意】但是这个在分析的时候要注意区间是会影响每个节点的，例如图中2放下后，5的新高度就变成了5。因此该问题根本不是每个节点累加，而是直接一次性的更新一个最高高度（让旧的高度再加上新的高度）

完整代码

class Solution {
public:
    vector<int> fallingSquares(vector<vector<int>>& positions) {
        vector<int>ans;
        for(auto &position:positions)
        {
            int left = position[0],right = position[0]+position[1];
            int val = position[1];
            int h = query(root,1,N,left,right-1);//先查出原来这个区域有多高
            update(root,1,N,left,right-1,val+h);//随后更新值直接是新高度
            ans.push_back(root->val);
        }
        return ans;
    }
    struct Node
    {
        int val,lazy;
        Node* left;
        Node* right;
        Node():val(0),lazy(0),left(nullptr),right(nullptr){}
    };
    int N = 1e8;
    Node* root = new Node();
    void update(Node* root,int start,int end, int l, int r,int val)
    {
        if(l<=start && r>=end) 
        {
            root->val = val;
            root->lazy = val;
            return; 
        }
        int mid = start+(end-start)/2;
        push_down(root);
        if(l<=mid) update(root->left,start,mid,l,r,val);
        if(r>mid)  update(root->right,mid+1,end,l,r,val);
        root->val = max(root->left->val,root->right->val);
    }
    int query(Node* root,int start,int end, int l, int r)
    {
        if(l<=start && r>=end)
        {
            return root->val;
        }
        int mid = start+(end-start)/2;
        push_down(root);
        int ans_l=0,ans_r=0;
        if(l<=mid) ans_l = query(root->left,start,mid,l,r);
        if(r>mid) ans_r = query(root->right,mid+1,end,l,r);
        return max(ans_l,ans_r);
    }
    void push_down(Node* root)
    {
        if(root->left==nullptr) root->left = new Node();
        if(root->right==nullptr) root->right = new Node();
        if(root->lazy==0) return;
        root->left->val =  root->lazy;
        root->right->val = root->lazy;
        root->left->lazy = root->lazy;
        root->right->lazy = root->lazy;
        root->lazy = 0;
    }
};

3 第三个题—732.我的日程表安排III（节点的值存放最大值的情形2）

题目

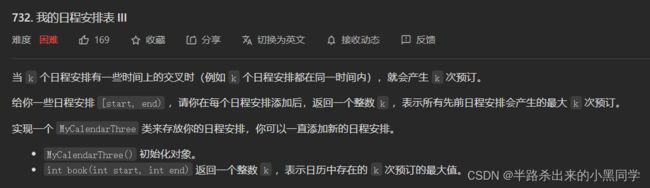
这个题目其实就明确告诉我们是需要求最大值，因此节点的值就需要存放最大值。但是这个跟上个题是有不同点的（他们可以重合！）。因此上一个题，是先查询到该区域的最大高度，然后一次性更新上最新的高度。而这个题可以重合，因此可以直接在符合区间的值直接
进行累加(update函数中)。

完整代码–线段树

class MyCalendarThree {
public:
    MyCalendarThree() {
    }
    
    int book(int start, int end) {
        update(root,0,N,start,end-1,1);//因为不需要知道之前的最大值，因此只需要更新
        return root->val;
    }
    struct Node
    {
        int val,lazy;
        Node* left;
        Node* right;
        Node():val(0),lazy(0),left(nullptr),right(nullptr){}
    };
    int N = 1e9;
    Node* root = new Node();
    void update(Node* root,int start,int end, int l, int r,int val)
    {
        if(l<=start && r>=end) 
        {
            root->val += val;
            root->lazy += val;
            return; 
        }
        int mid = start+(end-start)/2;
        push_down(root);
        if(l<=mid) update(root->left,start,mid,l,r,val);
        if(r>mid)  update(root->right,mid+1,end,l,r,val);
        root->val = max(root->left->val,root->right->val);
    }
    void push_down(Node* root)
    {
        if(root->left==nullptr) root->left = new Node();
        if(root->right==nullptr) root->right = new Node();
        if(root->lazy==0) return;
        root->left->val +=  root->lazy;
        root->right->val += root->lazy;
        root->left->lazy += root->lazy;
        root->right->lazy += root->lazy;
        root->lazy = 0;
    }
};

完整代码—差分数组(常用于不细查询一个区间的情况)

class MyCalendarThree {
public:
    map<int,int>diff;//差分数组
    MyCalendarThree() {
    }
    
    int book(int start, int end) {
        int left = start,right = end;
        diff[left]++;
        diff[right]--;
        int cur=0,max_v=0; 
        for(auto &a:diff)
        {
            cur += a.second;
            max_v = max(max_v,cur); 
        }
        return max_v;
    }
};

【差分法】其实本题就是将一个无限区间长的坐标，start到end之间的值+1，而end之后的再减去1，最终形成查分。为了快速找到并修改此处用到了差分数组的概念----查分数组常用于对区间内元素值的统一修改，也是通过有序集合来模拟区间的差法数组的。 其有两个特性：
1、nums[2] = nums[1] + diff[2] = diff[0] + diff[1] + diff[2];
根据差分数组各项的前缀和，即可还原出原数组的各值
2、而把 nums 数组中 [0,3] 范围到元素值都加 2，普通for循环十分麻烦，而差分法只用两步

diff[0] += 2;// 0 往后到值全部加 2
diff[4] -= 2;// 4 往后到值全部减 2！！注意哦这里是4
//这样就相当于3之后的没变，只有0-3被加了2

注意，本题中，差分有序集合,map分别存放的是坐标值以及其重叠值，而每次cur相加都是该坐标系下的值。注意差分数组就是默认左闭右开的，想改变【0，3】是要对0和4操作的！

四、线段树与差分数组

（PS：关于差分有序集合的解释看上面！！！）
同样能解决区间叠加问题，那么线段树和差分数组有什么不同之处呢？
显然，两者都能进行区间修改和区间查询，但优化方向存在差异。
对于差分数组，区间修改的时间复杂度为o(1)，而区间查询的时间复杂度为o(n)；而对于线段树，区间修改和查询的时间复杂度都为o(logn)。
因此，差分数组适用于多次区间修改，少量次查询的情况，同时适用于数据范围为1e7以内的问题；而线段树则适用于多次区间修改，多次查询的情况，且数据范围通常小于1e5。

五、总的线段树模板

1 易于理解，但是需要一个一个new的慢方法

套用模板的思想就是，只要能够在pushup函数表示的区间问题（如区间求和、最大值，而像众数（知道左右区间的众数，但你不知道左右区间的众数到底谁更多）此类就不可以套用），都可以对模板段落标注的地方进行改造套用模板。

	//1、先建立节点的数据结构
struct Node
    {
        int val,lazy;
        Node* left;
        Node* right;
        Node():val(0),lazy(0),left(nullptr),right(nullptr){}
    };
	//2、根据题目给的取值范围，确定好N，并建立好一个根节点，以供调用
    int N = 1e8;
    Node* root = new Node();
    //3、可以先写更新（反正和查询一个流程）
    void update(Node* root, int start, int end, int l, int r, int val) {
    /*1、这个写法表示每个节点里面存区间求和的形式，需要对应每次调用update时传入的val为该区间的点需要再加的值
    if (l <= start && end <= r) {
        root->val += (end - start + 1) * val;
        root->lazy += val;
        return ;
    }  */
    /*2、这个写法（详见第二题）表示每个节点里面存最大值的形式，需要对应每次调用update时传入的val为该区间新的高度
      if(l<=start && r>=end) 
        {
            root->val = val;
            root->lazy = val;
            return; 
        } */
				/*上面两个地方需要理解，根据题型所规定的节点值意义来具体定义 */
    int mid = start+(end - start)/2;
    // 下推标记
    pushDown(root, mid - start + 1, end - mid);
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (l <= mid) update(root->left, start, mid, l, r, val);
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (r > mid) update(root->right, mid + 1, end, l, r, val);
    // 将当前区间的值更新
     pushUp(root);
}
//4、可以再写查询（反正和更新一个流程）
int query(TreeNode* root, int start, int end, int l, int r) {
    if (l <= start && end <= r) return root->val;
    int mid = start+(end - start)/2;
    pushDown(root, mid - start + 1, end - mid);//注意这里的+1
    /*1、这里由于是查找区间和，因此答案理所当然是左边的值加上右边的值
    int ans = 0;
    if (l <= mid) ans += query(root->left, start, mid, l, r);
    if (r > mid) ans += query(root->right, mid + 1, end, l, r);
    */
    /*2、这里由于节点的值为最大值，因此答案理所当然是左边的值和右边的值大的那一个。
    int ans_l=0,ans_r=0;
    if(l<=mid) ans_l = query(root->left,start,mid,l,r);
    if(r>mid) ans_r = query(root->right,mid+1,end,l,r);
    int ans = max(ans_l,ans_r);
    */
               /*上面两个地方需要理解，根据题型所规定的节点值意义来具体定义 */
    return ans;
}
void pushdown(Node* root, int leftNum, int rightNum) {//下放懒标记
    if (root->left == nullptr) root->left = new TreeNode();
    if (root->right == nullptr) root->right = new TreeNode();
    if (root->lazy == 0) return ;
/*1、这里由于是求区间的和，因此肯定是lazy在乘上该区间个数，毕竟lazy其实是属于每个叶子节点的
    root->left->val += root->lazy * leftNum;
    root->right->val += root->lazy * rightNum;
    root>left->lazy += root->lazy;
   	root->right->lazy += root->lazy;
*/
/*2、这里由于节点的值为最大值，加上由于每次传进来的val都为更新后的值，因此这里直接等于，也不是累加了！
    root->left->val = root->lazy;
    root->right->val = root->lazy;
    root>left->lazy = root->lazy;
   	root->right->lazy = root->lazy;
*/
       /*上面四个地方需要理解，根据题型所规定的节点值意义来具体定义 */
    root->lazy = 0;
}
void pushUp(Node* root)
{
	/*此处就不过多解释了*/
	root->val = root->left->val+root->right->val;
	// or root->val = max(root->left->val, root->right->val);
}

2 相较难理解，但是能够快很多的数组方法

其中root指针一律由整型int标号index来代替。即root->left = tree[index].left

	//1、先建立节点的数据结构
struct Node
    {
        int val,lazy;
        int left,right;
        Node():val(0),lazy(0),left(0),right(0){}//依旧初始0即可
    };
	//2、根据题目给的取值范围，确定好N，并提前建立好申请过内存的一个数组
    constexpr static int N = 1e8;
    constexpr static int M = 500000;这里就是提前申请的内存数，如果WA了，此处就可以在修改
    Node Tree[M];
    int idx = 0;//这个是精髓，它会和pushdown的第一步一起完成动态开点
    //3、可以先写更新（反正和查询一个流程）
    void update(int index, int start, int end, int l, int r, int val) {
    /*1、这个写法表示每个节点里面存区间求和的形式，需要对应每次调用update时传入的val为该区间的点需要再加的值
    if (l <= start && end <= r) {
        tree[index].val += (end - start + 1) * val;
        tree[index].lazy += val;
        return ;
    }  */
    /*2、这个写法（详见第二题）表示每个节点里面存最大值的形式，需要对应每次调用update时传入的val为该区间新的高度
      if(l<=start && r>=end) 
        {
            tree[index].val = val;
            tree[index].lazy = val;
            return; 
        } */
				/*上面两个地方需要理解，根据题型所规定的节点值意义来具体定义 */
    int mid = start+(end - start)/2;
    // 下推标记
    pushDown(index, mid - start + 1, end - mid);
    // [start, mid] 和 [l, r] 可能有交集，遍历左孩子区间
    if (l <= mid) update(tree[index].left, start, mid, l, r, val);
    // [mid + 1, end] 和 [l, r] 可能有交集，遍历右孩子区间
    if (r > mid) update(tree[index].right, mid + 1, end, l, r, val);
    // 将当前区间的值更新--这一步一定要记住，已经不能直接对Tree[index]操作了，需要结合左右孩子
     pushUp(index);
}
//4、可以再写查询（反正和更新一个流程）
int query(int index, int start, int end, int l, int r) {
    if (l <= start && end <= r) return tree[index].val;
    int mid = start+(end - start)/2;
    pushDown(index, mid - start + 1, end - mid);//注意这里的+1
    /*1、这里由于是查找区间和，因此答案理所当然是左边的值加上右边的值
    int ans = 0;
    if (l <= mid) ans += query(tree[index].left, start, mid, l, r);
    if (r > mid) ans += query(tree[index].right, mid + 1, end, l, r);
    */
    /*2、这里由于节点的值为最大值，因此答案理所当然是左边的值和右边的值大的那一个。
    int ans_l=0,ans_r=0;
    if(l<=mid) ans_l = query(tree[index].left,start,mid,l,r);
    if(r>mid) ans_r = query(tree[index].right,mid+1,end,l,r);
    int ans = max(ans_l,ans_r);
    */
               /*上面两个地方需要理解，根据题型所规定的节点值意义来具体定义 */
    return ans;
}
void pushdown(int index, int leftNum, int rightNum) {//下放懒标记
    if (tree[index].left == 0) tree[index].left = ++idx;//注意这里是idx，其会随着动态开点而不断变化
    if (tree[index].right == 0) tree[index].right = ++idx;
    if (tree[index].lazy == 0) return ;
/*1、这里由于是求区间的和，因此肯定是lazy在乘上该区间个数，毕竟lazy其实是属于每个叶子节点的
    tree[tree[index].left].val += root->lazy * leftNum;
    tree[tree[index].right].val += root->lazy * rightNum;
    tree[tree[index].left].lazy += root->lazy;
   	tree[tree[index].right].lazy += root->lazy;
*/
/*2、这里由于节点的值为最大值，加上由于每次传进来的val都为更新后的值，因此这里直接等于，也不是累加了！
    tree[tree[index].left].val = root->lazy;
    tree[tree[index].right].val = root->lazy;
    tree[tree[index].left].lazy = root->lazy;
   	tree[tree[index].right].lazy = root->lazy;
*/
       /*上面四个地方需要理解，根据题型所规定的节点值意义来具体定义 */
    tree[index].lazy = 0;
}
void pushUp(Node* root)
{
	/*此处就不过多解释了*/
	root->val = root->left->val+root->right->val;
	// or root->val = max(root->left->val, root->right->val);
}

引用

1、https://leetcode.cn/problems/range-module/solution/by-lfool-eo50/
LFool大佬写的线段树详解「汇总级别整理 」
2、https://blog.csdn.net/qiancm/article/details/118763889
黑马星云大佬的线段树详解C++
3、力扣大佬hqztrue和杯杯回应的讨论
https://leetcode.cn/circle/discuss/0vjSA9/