day17二叉搜索树中的最小绝对差&二叉搜索树中的众数&二叉树的最近公共节点

        继续学习二叉搜索树的应用，今天题目比昨天的好理解。

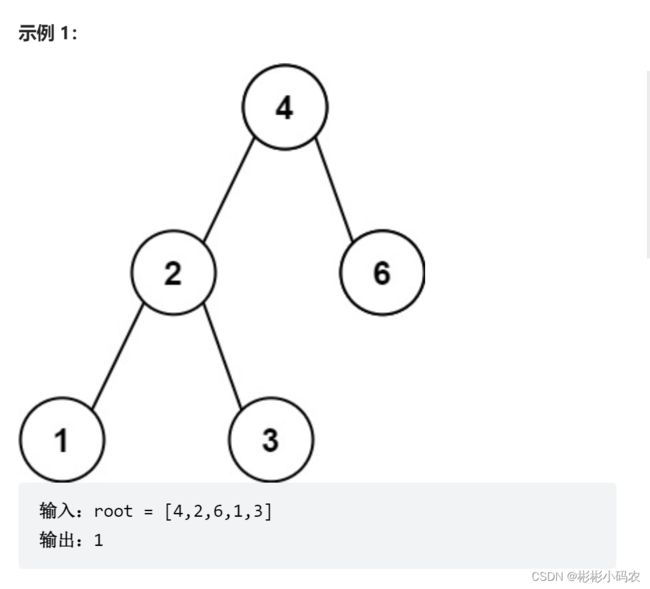
1.力扣530（二叉搜索树中的最小绝对差）

                               

        本题我们利用双指针来遍历二叉树，昨天的题目中也利用到了，也就是二叉树在中序遍历的时候会数值会单调递增，而我们定义一个节点类型的指针，用来指向当前遍历节点的前一个节点，以此来比较下数值。下面利用递归三部曲来解决问题：

• 确定参数和返回值：因为我们定义了一个全局变量来存储最小值，所以我么你这里不需要返回值。

   public void getMin(TreeNode root) 

• 确定结束条件：这里直接变量到重点就进行返回。

        if(root==null){
            return;
        }

• 确定单层的逻辑：我们采用中序遍历，所以写出中序遍历的递归后，在中位置处增加我们的逻辑，进行数值相减的操作，然后取最小值

        //左
        getMin(root.left);
        //中
        if(pre!=null){
            res = Math.min(res,root.val-pre.val);
        }
        pre = root;
        //右
        getMin(root.right);

整体代码：

    int res=Integer.MAX_VALUE;
    TreeNode pre =null;
    public int getMinimumDifference(TreeNode root) {
        getMin(root);
        return res;
    }
    public void getMin(TreeNode root) {
        if(root==null){
            return;
        }
        //左
        getMin(root.left);
        //中
        if(pre!=null){
            res = Math.min(res,root.val-pre.val);
        }
        pre = root;
        //右
        getMin(root.right);
    }

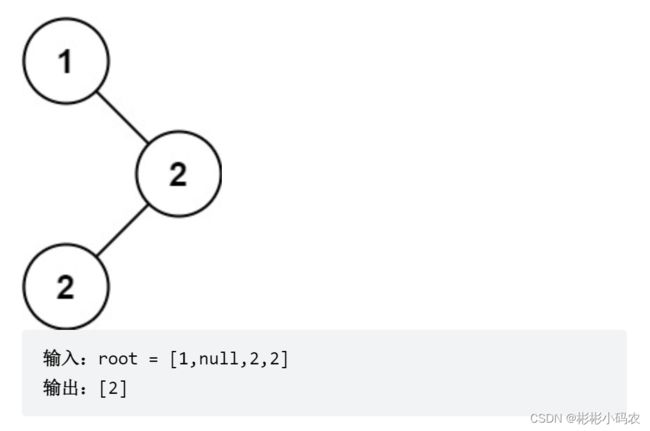
2.力扣501（二叉搜索树中的众数）

                

        其他逻辑不算难，最主要这里面有动态处理的小技巧。我们继续利用中序遍历来遍历二叉搜索树，此时我们需要定义几个全局变量，要有指向前一个节点的头指针，记录出现次数的count，还有记录出现次数最多的次数maxValue，然后进行递归，若pre和root相同就count++，若不相同就重新赋值count=1操作，如果count的值等于maxValue，就是另一个众数所以入队，若pre和root相同，我们就对count进行加1，然后清空集合并重新存储。下面用递归三部曲来实现：

• 确定参数和返回值：这里我们定义了全局变量，不需要返回值

    public void find(TreeNode root)

• 确定结束条件：若为空节点就进行返回

        if(root==null){
            return;
        }

• 确定单层逻辑：进行左右子树递归，中的操作是先对前一个节点和root节点进行判断，若相同就count++，不相同就赋值为count=1；接下来是动态更新的过程，进行判断count和maxValue的值，若相等就相加，大于就清空集合并重新存储。

        //左
        find(root.left);
        //中
        if(pre==null){
            count=1;
        }else if(pre.val==root.val){
            count++;
        }else{
            count=1;
        }
        if(count==maxValue){
            resList.add(root.val);
        }
        if(count>maxValue){
            resList.clear();
            resList.add(root.val);
            maxValue=count;
        }
        pre = root;
        find(root.right);

整体代码：

    int cnt=0;
    int maxValue = 0;
    List resList = new ArrayList();
    int count=0; 
    TreeNode pre =null;
    public int[] findMode(TreeNode root) {
        find(root);
        int[] arr = new int[resList.size()];
        for(int i=0;imaxValue){
            resList.clear();
            resList.add(root.val);
            maxValue=count;
        }
        pre = root;
        find(root.right);
    }

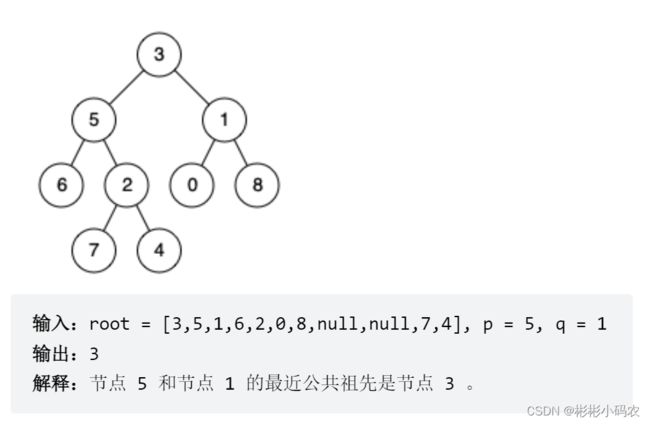
3.力扣236（二叉树的最近公共节点）

        

         本题求得是最近得公共节点，因为本题最起码就根节点这一个公共节点，本题利用后续遍历，因为我们需要先遍历左右子树，最终进行判断左右子树是否不为空。下面是递归三部曲：

• 确定参数和返回值：参数就是节点和p，q，返回值就是公共祖节点

    public TreeNode lowestCommon(TreeNode root, TreeNode p, TreeNode q) 

• 确定结束条件：返回两种情况，一种是没有找到节点，就返回null，若找到就返回此节点

        if(root==null){
            return root;
        }
        if(root==p||root==q){
            return root;
        }

• 确定单层逻辑：我们需要对左右子树得返回值进行判断，若左右子树都不为空，则说明找到了值，若左或者右不为空得话，就返回不为空得那个节点，交给上一层去判断公共祖节点

        //左
        TreeNode left = lowestCommon(root.left,p,q);
        //右
        TreeNode right = lowestCommon(root.right,p,q);
        //中
        if(left!=null&&right!=null){
            return root;
        }else if(left!=null&&right==null){
            return left;
        }else{
            return right;
        }

整体代码：

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return lowestCommon(root,p,q);
    }

    public TreeNode lowestCommon(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null){
            return root;
        }
        if(root==p||root==q){
            return root;
        }
        //左
        TreeNode left = lowestCommon(root.left,p,q);
        //右
        TreeNode right = lowestCommon(root.right,p,q);
        //中
        if(left!=null&&right!=null){
            return root;
        }else if(left!=null&&right==null){
            return left;
        }else{
            return right;
        }
    }