考研：数学二做题套路

文章中的□，代表广义化，就是什么都可以往里面填（但是每个公式中，□的值必须相同，假设一个公式中有两个□，不可以第一个填x第二个填y）

每个类型，都会先总结公式和套路，然后放例题，一般来讲直接看公式很难完全看懂，需要配合例题来理解

0、必会高中公式

完全平方公式（3次方）：$a^3\pm b^3=(a\pm b)(a^2\mp ab+b^2)$

log / ln 相关公式

$\{\begin{array}{ll}lnA\cdot B& =lnA+lnB\\ ln\frac{A}{B}& =lnA-lnB\\ ln{A}^B& =B\cdot lnA\\ {\log }_{a}b& =\frac{lo{g}_{c}b}{lo{g}_{c}a}\\ lo{g}_{a}a& =1\\ 对数恒等式：a^{lo{g}_{a}N}& =N(a>0,a\ne 1,N>0)\end{array}$

三角公式

$\begin{array}{r}\{\begin{array}{l}二角和差：\{\begin{array}{l}cos(\alpha \pm \beta )=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \\ sin(\alpha \pm \beta )=sin\alpha \cdot cos\alpha \pm cos\beta \cdot cos\beta \\ tan(\alpha \pm \beta )=\frac{tan\alpha \pm tan\beta }{1\mp tan\alpha tan\beta }\end{array}\\ 倍角公式：\{\begin{array}{l}由二角和差公式推导(例如sin2\alpha =sin(\alpha +\alpha ))\\ sin2\alpha =2sin\alpha cos\alpha =sin(\alpha +\alpha )=sin\alpha cos\alpha +sin\alpha cos\alpha \\ cos2\alpha =co{s}^2\alpha -si{n}^2\alpha =2co{s}^2\alpha -1=1-2si{n}^2\alpha \\ tan2\alpha =\frac{2tan\alpha }{1-ta{n}^2\alpha }\end{array}\\ 降次公式：\{\begin{array}{l}由倍角公式推导，例如cos2\alpha =1-2si{n}^2\alpha 则si{n}^2\alpha =\frac{1-cos(2\alpha )}{2}\\ si{n}^2\theta =\frac{1-cos(2\theta )}{2}\\ \\ co{s}^2\theta =\frac{1+cos(2\theta )}{2}\\ \\ ta{n}^2\theta =\frac{si{n}^2\theta }{co{s}^2\theta }=\frac{1-cos(2\theta )}{1+cos(2\theta )}\end{array}\\ 半角公式：\{\begin{array}{l}由降次公式推导，例如si{n}^2\theta =\frac{1-cos(2\theta )}{2}则si{n}^2\frac{x}{2}=\frac{1-cos(2\cdot \frac{x}{2})}{2}然后可以开平方得到sin\frac{x}{2}\\ sin\frac{x}{2}=\pm \sqrt{\frac{1-cosx}{2}}\\ cos\frac{x}{2}=\pm \sqrt{\frac{1+cosx}{2}}\\ tan\frac{x}{2}=\pm \sqrt{\frac{1-cosx}{1+cosx}}\end{array}\\ 函数公式：\{\begin{array}{l}si{n}^{2}x+co{s}^{2}x=1\\ 1+ta{n}^{2}x=se{c}^{2}x，(\because si{n}^{2}x+co{s}^{2}x=1\to \frac{si{n}^{2}x}{co{s}^{2}x}+\frac{co{s}^{2}x}{co{s}^{2}x}=\frac{1}{co{s}^{2}x}=ta{n}^{2}x+1=se{c}^{2}x)\end{array}\end{array}\\ \end{array}$

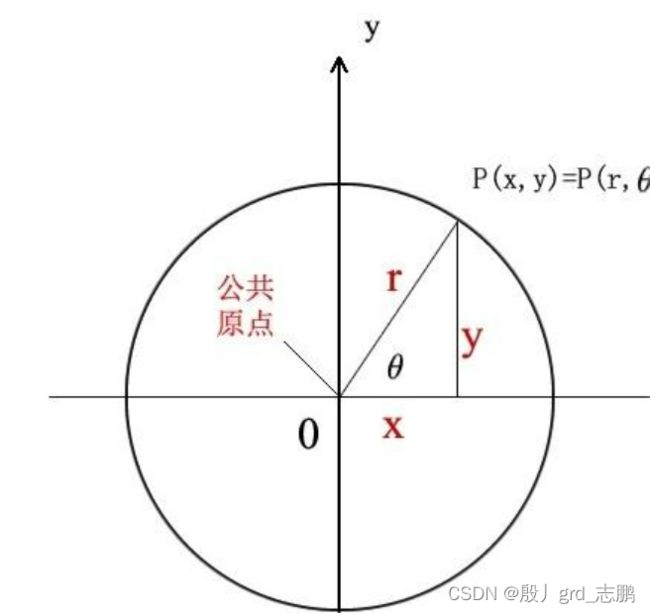
极坐标

一般，都会将r写成$\rho$来让读者知道，是极坐标，而不是圆形，但是要知道$\rho$，代表的就是r这条半径的长度

一、高数

$\begin{array}{r}\lim \int \to \frac{}{}\sim \mp \pm \alpha \beta \theta \rho \cdot \\ \end{array}$

0.0导数公式

求导法则

$\{\begin{array}{l}基本求导法则：\{\begin{array}{l}1、(u\pm v{)}^{\prime }=u^{\prime }\pm v^{\prime }\\ 2、(u\cdot v{)}^{\prime }=u^{\prime }\cdot v+v^{\prime }\cdot u\\ 3、(\frac{u}{v}{)}^{\prime }=\frac{v\cdot u^{\prime }-u\cdot v^{\prime }}{v^2},v\ne 0\end{array}\\ \\ 反函数求导法则\{\begin{array}{l}(反函数{)}^{\prime }=\frac{1}{(原函数{)}^{\prime }}\end{array}\\ \\ \end{array}$

基本导数公式，证明过程略

$\{\begin{array}{llcc}1、(C{)}^{\prime }=0& 2、(x^a{)}^{\prime }=a{x}^{a-1}& 2.1、(\frac{1}{x}{)}^{\prime }=-(\frac{1}{x^2})& 2.2、(\sqrt{x}{)}^{\prime }=\frac{1}{2\sqrt{x}}\\ 3、(a^x{)}^{\prime }=(a^x)lna& 3.3、(e^x{)}^{\prime }=e^x& & \\ 4、(lo{g}_{a}x{)}^{\prime }=\frac{1}{xlna}& 4.1、(lnx{)}^{\prime }=\frac{1}{x}& & \\ & & & \end{array}$

三角函数求导，证明过程给出部分

$\{\begin{array}{llcc}& 1、(sinx{)}^{\prime }=cosx& 2、(cosx{)}^{\prime }=-sinx& 3、(tanx{)}^{\prime }=se{c}^{2}x\\ & 4、(cotx{)}^{\prime }=-cs{c}^{2}x& 5、(secx{)}^{\prime }=secx\cdot tanx& 6、(cscx{)}^{\prime }=-cscx\cdot cotx\\ & & & \end{array}$

证明过程如下：

$\{\begin{array}{l}1、(tanx{)}^{\prime }=(\frac{sinx}{cosx}{)}^{\prime }=\frac{cosx\cdot cosx-sinx\cdot (-sinx)}{co{s}^{2}x}=\frac{1}{co{s}^{2}x}=se{c}^{2}x\\ \\ 2、(cotx{)}^{\prime }=(\frac{cosx}{sinx}{)}^{\prime }=\frac{sinx\cdot (-sinx)-cosx\cdot cosx}{si{n}^{2}x}=-\frac{1}{si{n}^{2}x}=-cs{c}^{2}x\\ \\ 3、(secx{)}^{\prime }=(\frac{1}{cosx}{)}^{\prime }=\frac{cosx\cdot 0-1\cdot (-sinx)}{co{s}^{2}x}=\frac{sinx}{co{s}^{2}x}=secx\cdot tanx\\ \\ 4、(cscx{)}^{\prime }=(\frac{1}{sinx}{)}^{\prime }=\frac{sinx\cdot 0-1\cdot (cosx)}{si{n}^{2}x}=\frac{-cosx}{si{n}^{2}x}=-cscx\cdot cotx\\ \\ 5、(sinx{)}^{\prime }=(\frac{1}{\frac{1}{sinx}}{)}^{\prime }=(\frac{1}{cscx}{)}^{\prime }=\frac{cscx\cdot 0-1\cdot (-cscx\cdot cotx)}{cs{c}^{2}x}=\frac{cotx}{cscx}=\frac{cosx}{sinx}\cdot sinx=cosx\\ \end{array}$

反三角函数求导

$\{\begin{array}{llc}& 1、(arctanx{)}^{\prime }=\frac{1}{1+x^2}& 2、(arccot{)}^{\prime }=-\frac{1}{1+x^2}\\ & 3、(arcsinx{)}^{\prime }=\frac{1}{\sqrt{1-x^2}}& 4、(arccosx{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}\\ & & \end{array}$

证明过程如下：$(反函数{)}^{\prime }=\frac{1}{(原函数{)}^{\prime }}$

$\{\begin{array}{l}1、(arcsinx{)}^{\prime }(x\in [-1,1])=\{\begin{array}{l}\because y=arcsinx\therefore 原函数为x=siny且y\in [-\frac{\pi }{2},\frac{\pi }{2}]\\ \frac{dy}{dx}=(arcsinx{)}^{\prime }=\frac{1}{(siny{)}^{\prime }}=\frac{1}{cosy}=\frac{1}{\sqrt{1-si{n}^{2}y}}\\ \because x=siny\therefore si{n}^{2}y=x^2，\frac{1}{\sqrt{1-si{n}^{2}y}}=\frac{1}{\sqrt{1-x^2}}\end{array}\\ 2、(arctanx{)}^{\prime }=\{\begin{array}{l}\because y=arctanx\therefore x=tany\\ \frac{dy}{dx}=(arctanx{)}^{\prime }=\frac{1}{(tany{)}^{\prime }}=\frac{1}{se{c}^{2}y}=\frac{1}{1+ta{n}^{2}y}=\frac{1}{1+x^2}\end{array}\\ \end{array}$

常用的复合函数求导（现场求费时间，最好记住）

$\{\begin{array}{llc}& 1、(ln|cosx|{)}^{\prime }=-tanx& 2、(ln|sinx|{)}^{\prime }=cotx\\ & 3、(ln|secx+tanx|{)}^{\prime }=secx& 4、(ln|cscx-cotx|{)}^{\prime }=cscx\\ & 5、(ln|x+\sqrt{x^2\pm a^2}|{)}^{\prime }=\frac{1}{\sqrt{x^2\pm a^2}}& \\ & & \end{array}$

证明过程如下:

$\{\begin{array}{l}1、(ln|cosx|{)}^{\prime }=\frac{1}{cosx}\cdot (-sinx)=-tanx\\ 2、(ln|sinx|{)}^{\prime }=\frac{1}{sinx}\cdot (cosx)=cotx\\ 3、(ln|cscx-cotx|{)}^{\prime }=\frac{1}{cscx-cotx}\cdot (-cscxcotx+cs{c}^{2}x)=\frac{cscx(cscx-cotx)}{cscx-cotx}=cscx\\ 4、(ln|secx+tanx|{)}^{\prime }=\frac{1}{secx+tanx}\cdot (secxtanx+se{c}^{2}x)=\frac{secx(tanx+secx)}{secx+tanx}=secx\\ 5、(ln|x+\sqrt{x^2\pm a^2}|{)}^{\prime }=\frac{1}{x+\sqrt{x^2\pm a^2}}\cdot (1+\frac{1}{2\sqrt{x^2\pm a^2}}\cdot 2x)=\frac{1}{x+\sqrt{x^2\pm a^2}}\cdot (\frac{\sqrt{x^2\pm a^2}}{\sqrt{x^2\pm a^2}}+\frac{x}{\sqrt{x^2\pm a^2}})\\ =\frac{1}{x+\sqrt{x^2\pm a^2}}\cdot (\frac{\sqrt{x^2\pm a^2}+x}{\sqrt{x^2\pm a^2}})=\frac{1}{\sqrt{x^2\pm a^2}}\\ \end{array}$

1.极限

求极限，要先判断是什么类型，就是把极限带进去，看看是哪种类型，然后选择方法做出，或者化简为$\frac{0}{0}（可以等价代换和洛必达）或\frac{\infty }{\infty }型（洛必达或抓大头）,$

1.0.0 极限4则运算

$\{\begin{array}{l}设\underset{x\to \square }{\lim }f(x)=A,\underset{x\to \square }{\lim }g(x)=B\\ \underset{x\to \square }{\lim }(f(x)\pm g(x))=A\pm B\\ \underset{x\to \square }{\lim }f(x)\cdot g(x)=A\cdot B\\ \underset{x\to \square }{\lim }\frac{f(x)}{g(x)}=\frac{A}{B}(B\ne 0)\end{array}$

1.0.1 等价代换

等价代换是用泰勒展开式推导出来的，下面是做题经常会用到的，记下来会很大程度提高做题效率，而不用每次都用泰勒展开式推导。

$\{\begin{array}{ll}1、sinx\sim x& ：arcsinx\sim x：tanx\sim x：arctanx\sim x\\ 2、a^x-1\sim xlna& ：e^x-1\sim x：ln(1+x)\sim x：(1+x{)}^{\alpha }-1\sim \alpha x\stackrel{常用形式}{}(\sqrt{1+x}-1\sim \frac{1}{2}x)\\ 3、x-ln(1+x)\sim \frac{1}{2}{x}^2& ：1-co{s}^{\alpha }x\sim \frac{\alpha }{2}{x}^2\stackrel{常用形式}{}1-cosx\sim \frac{1}{2}{x}^2\\ 4、x-sinx\sim \frac{1}{6}{x}^3& ：x-arcsinx\sim -\frac{1}{6}{x}^3\\ 5、x-tanx\sim -\frac{1}{3}{x}^3& ：x-arcthanx\sim \frac{1}{3}{x}^3\\ 6、tanx-sinx\sim \frac{1}{2}{x}^3& ：arctanx-arcsinx\sim -\frac{1}{2}{x}^3\end{array}$
注意：上面公式中的所有x，都可以看做任意变量□，也就是填什么都行，比如把所有x都换成sinx，例如：$e^x-1\sim x$ 换成 $e^{sinx}-1\sim sinx$也一样成立。
注意2：上面公式 “~” 两边都可以同乘同除（比如两边同乘-1），灵活使用不要死板

1. 什么是等价为最简形式

当$x\to 0$时，我们知道$e^{sinx}-1\sim sinx$，但此时我们没有化为最简，因为sin x还有$sinx\sim x$，而x是最简形式（无法继续向下代换），所以当$e^{sinx}-1\sim x$才称 等价为了最简形式，而$e^{sinx}-1\sim sinx$ ，因为$sinx$还可以继续等价为x，所以不是最简形式

2. 乘除可以等价代换，但是加减只能在特定条件下才可以等价代换，特定条件如下：

1. 在等价成最简形式后，无法抵消成0，加减可以代换（不推荐）
   $\{\begin{array}{l}\underset{x\to 0}{\lim }\frac{tanx-sinx}{x^3}\stackrel{tanx和sinx等价最简形式都是x}{}\underset{x\to 0}{\lim }\frac{x-x}{x^3}分子消为0，不可代换\\ 因为x-tanx\sim -\frac{1}{3}{x}^3\stackrel{两边乘-1}{}tanx-x\sim \frac{1}{3}{x}^3\\ 同理sinx-x\sim -\frac{1}{6}{x}^3为最简形式\\ 则：\underset{x\to 0}{\lim }\frac{tanx-sinx}{x^3}\stackrel{配分（加一个x再减一个x）}{}\underset{x\to 0}{\lim }\frac{(tanx-x)-(sinx-x)}{x^3}\\ =\underset{x\to 0}{\lim }\frac{(\frac{1}{3}{x}^3)-(-\frac{1}{6}{x}^3)}{x^3}=\frac{1}{2}\\ \end{array}$
2. 等价成最简形式后，为了描述方便，这里设+/-号两边等价后最简形式为□和△，则满足以下条件可代换：

1. 符号为减号“-”时：$\underset{x\to ▽}{\lim }\frac{\square }{△}极限存在，且不等于1$。则可以代换
2. 符号为加号“+”时：$\underset{x\to ▽}{\lim }\frac{\square }{△}极限存在，且不等于-1$。则可以代换

例子：$\underset{x\to 0}{\lim }\frac{tanx-sinx}{x^3}$ 都等价为x最简形式后，因为符号为减号“-”，则判断是否$\underset{x\to ▽}{\lim }\frac{\square }{△}极限存在，且不等于1。$此时代入发现$\underset{x\to 0}{\lim }\frac{x}{x}=1，因此不可代换$

1.0.2 泰勒展开

泰勒公式具体展开到多少项：反正展开后不要比分母大，比如分母是x^4,你展开后，最高次分子就不要超过4次，只能比4次小或等于4次。

公式：$f(x)=f(x_0)+\frac{f^{{}^{\prime }}(x_0)}{1!}\cdot (x-x_0{)}^1+\frac{f^{{}^{\prime \prime }}(x_0)}{2!}\cdot (x-x_0{)}^2+\frac{f^{{}^{\prime \prime \prime }}(x_0)}{3!}\cdot (x-x_0{)}^3+...+\frac{f^n(x_0)}{n!}\cdot (x-x_0{)}^n+RN(余项O((x-x^0{)}^n))$
考研涉及到很多需要的泰勒展开来做题，你可以只记住上面这个公式，然后现场推导。但是考研题量大，时间紧，我们需要保证一秒推导完成。那此时记下来才是更好的选择。下面的常用展开，只需记住4个，剩下的都可以通过这4个快速推导。注意：所有展开只考虑$x_0=0$时

1. 需要记忆的4个：$\begin{array}{r}\{\begin{array}{l}1、e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...+\frac{x^n}{n!}+O(x^n)\\ 2、sinx=x-\frac{x^3}{3!}+\frac{x^5}{5!}-...+\frac{(-1{)}^n{x}^{2n+1}}{(2n+1)!}+O(x^{2n+1})\\ 3、\frac{1}{1-x}=1+x+x^2+x^3+...+x^n+O(x^n)\\ 4、(1+x{)}^a=1+ax+\frac{a(a-1)}{2!}{x}^2+\frac{a(a-1)(a-2)}{3!}{x}^3+...+\frac{\alpha (\alpha -1)...(\alpha -n+1)}{n!}+O(x^n)\end{array}\\ \end{array}$
2. 可推导的4个$\begin{array}{r}\{\begin{array}{l}1、cosx=(sinx{)}^{{}^{\prime }}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-...+\frac{(-1{)}^n{x}^{2n}}{(2n)!}+O(x^{2n})没错，就是根据上面sinx的公式，每一项求导\\ 2、\frac{1}{1+x}=\frac{1}{1-(-x)}=1-x+x^2-x^3+...+(-1{)}^n{x}^n+O(x^n)没错，就是把分母的1-x换成1-(-x)\\ 3、ln(1+x)=\int \frac{1}{1+x}dx=x-\frac{1}{2}{x}^2+\frac{1}{3}{x}^3-\frac{1}{4}{x}^4+...+(-1{)}^n\frac{1}{n+1}{x}^{n+1}+O(x^n)没错，就是把\frac{1}{1+x}每项求积分\\ 4、ln(1-x)=ln(1+(-x))=-x-\frac{1}{2}{x}^2-\frac{1}{3}{x}^3-\frac{1}{4}{x}^4+...+(-1{)}^n\frac{1}{n+1}(-x{)}^{n+1}+O(x^n)没错，就是把1-x换成1+(-x)\\ 5、-ln(1-x)=x+\frac{1}{2}{x}^2+\frac{1}{3}{x}^3+\frac{1}{4}{x}^4+...+(-(-1{)}^n)\frac{1}{n+1}(-x{)}^{n+1}+O(x^n)我怕你们翻不过来，泰勒展开式也可以两边同乘同除（比如同乘-1）\end{array}\\ \end{array}$
3. 拔高的3个（不在考纲，但是算极限等价无穷小很好用），最好背下来，这3个直接用泰勒展开式推导非常麻烦$\begin{array}{r}\{\begin{array}{l}1、tanx=x+\frac{1}{3}{x}^3+\frac{2}{15}{x}^5+\frac{17}{315}{x}^7+...+O(x^n)记住前两项就够用\\ 2、arctanx=x-\frac{1}{3}{x}^3+\frac{1}{5}{x}^5+...+O(x^n)写3项是为了告诉大家，不是tanx推过来的\\ 3、arcsinx=x+\frac{1}{6}{x}^3+\frac{3}{40}{x}^5+...+O(x^n)没错，就是把\frac{1}{1+x}每项求积分\end{array}\\ \end{array}$

1.0.3 拉格朗日中值定理

$\begin{array}{r}拉格朗日中值定理：\{\begin{array}{l}f(b)-f(a)=f^{{}^{\prime }}(\xi )\cdot (b-a)\\ 其中\xi 位于a,b之间，根据夹逼准则，a和b都趋向于0时，\xi 也趋于0\\ a<\xi <b\end{array}\\ \end{array}$

1.0.4积分中值定理

$\begin{array}{r}积分中值定理：\{\begin{array}{l}{\int }_a^{b}f(x)dx=f(\xi )\cdot (b-a),a<\xi <b.\end{array}\\ \end{array}$

1.1.1 $\frac{0}{0}$型

方法

1. 洛必达(看书)
2. 等价代换(前面总结了)
3. 泰勒展开(前面终结了)
4. 导数定义（看书）
5. 拉格朗日中值定理(前面总结了)
6. 抓大头：和$\frac{\infty }{\infty }型$一样，也可以抓大头，只不过在x$\to 0$时，$x^2>x^3$，这和x$\to \infty$时正好相反

例题
https://blog.csdn.net/grd_java/article/details/132735036

1.1.2 $\frac{\infty }{\infty }型$

方法

1. $\frac{\infty }{\infty }型抓类型/大头\{\begin{array}{l}先抓类型：对数函数{\log }_{a}x\ll 幂函数x^{\alpha }\ll 指数函数a^x(\ll 表示远远小于)\\ 类型相同，抓大头\{\begin{array}{l}{x}^{\alpha }或a^x抓高次，留下高次，其它可以省略\\ log对数，抓底数，留下底数大，其它可以省略\end{array}\\ 最后比较：\{\begin{array}{l}\frac{大}{小}=\infty (例如\frac{a^x}{x^{\alpha }}=\infty 、\frac{x^5}{x^4+x^3}\stackrel{分母抓大头，留下高次}{}=\frac{x^5}{x^4}=\infty )\\ \\ \frac{小}{大}=0(例如\frac{x^{\alpha }}{a^x}=0)\end{array}\\ \end{array}$
2. 洛必达

1.2.1 $\infty -\infty 和0\cdot \infty$

方法套路($\infty -\infty 怎么做0\cdot \infty 就怎么做$)

$\infty -\infty \{\begin{array}{l}有分母通分\\ 无分母造分母\{\begin{array}{l}有理化\\ 倒代换\end{array}\\ 注意：\{\begin{array}{l}如果0或\infty 有一个远远大于另一个。那么大的是啥就是啥。\\ 例如\alpha >0,x\to 0^{+}.则x^{\alpha }\to 0.ln(x^2+x)\to \infty 。\\ 那么\underset{x\to 0^{+}}{\lim }{x}^{\alpha }ln(x^2+x)为0\cdot \infty ，但是lnx远远小于\ll x^a,所以\underset{x\to 0^{+}}{\lim }{x}^{\alpha }ln(x^2+x)=0\end{array}\end{array}$
泰勒公式
拉格朗日中值定理

例题
https://blog.csdn.net/grd_java/article/details/132753102

1.1.1 $1^{\infty }$型

方法

1. $恒等变形\{\begin{array}{llc}{e}^{\ln \square }& \text{=}& \square \\ ln{e}^{\square }& \text{=}& \square \end{array}$

1. $log/ln相关公式\{\begin{array}{ll}lnA\cdot B& =lnA+lnB\\ ln\frac{A}{B}& =lnA-lnB\\ ln{A}^B& =B\cdot lnA\\ {\log }_{a}b& =\frac{lo{g}_{c}b}{lo{g}_{c}a}\end{array}$
2. $技巧：利用等价无穷\{\begin{array}{l}当\underset{△\to 1}{\lim }时有ln△\sim △-1\sim 0:(因为ln1=0，1-1=0)\\ 则\underset{△\to 1}{\lim }时有ln△=ln[1+△-1]\sim △-1：（因为ln[1+△-1]\sim ln[1+0]=ln1=0）\end{array}$
3. $综合利用就有\lim u^v=\lim e^{ln{u}^v}=lim{e}^{v\cdot lnu}=\lim e^{v\cdot (u-1)}=e^{\lim v(u-1)}:(因为是1^{\infty }型，u无限趋近于1，则lnu=ln[1+u-1]\sim u-1)$

2. $模板法(武忠祥教授的三步走)：遇到1^{\infty }极限直接\lim u^v=e^{\lim 指数(底-1)}=e^{\lim v(u-1)}:(可以发现就是上面的恒等变形法的综合利用，大家觉得上面理解不了可以直接记住这个)$
3. $凑第二个重要极限\underset{\square \to 0}{\lim }(1+\square {)}^{\frac{1}{\square }}=e：此方法已经不常用了，就是想方设法将原题凑成这个极限$

例题
https://blog.csdn.net/grd_java/article/details/132753237

1.1.2 ${\infty }^0/0^0$

方法套路

和$1^{\infty }$型一样，但是只能用恒等变形法

例题
https://blog.csdn.net/grd_java/article/details/132753296

1.1.3含变限积分的

化简，就是一种化简题目的方法，一般都需要先化简，再用公式求

$\{\begin{array}{l}1、{\int }_{sinx}^{0}f(t)dt=-{\int }_0^{sinx}f(t)dt；sinx\ge 0，遇到上限(sinx)在下面的时候，可以通过提一个负号，将上限放到上面\\ \\ 2、{\int }_{sinx}^{x^2}f(t)dt={\int }_{sinx}^{0}f(t)dt+{\int }_0^{x^2}f(t)dt；可以选择上限和下限之间的常数，来分成两个积分。不用考虑上下限到底颠没颠倒\\ \end{array}$

求变限积分导数的公式

$\{\begin{array}{l}大家体会一下规律，x^{{}^{\prime }}=1,常数a^{{}^{�}}\end{array}$