只使用位运算实现加减乘除
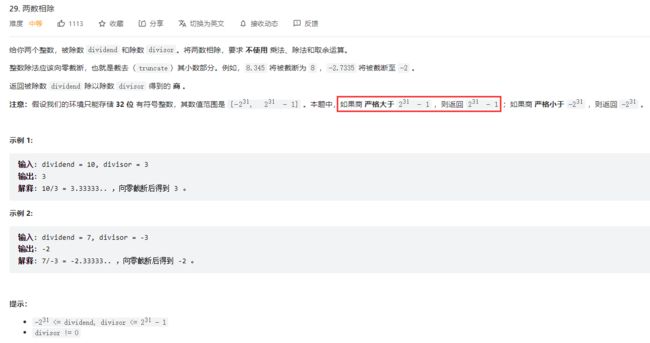
在线OJ: LeetCode 29. 两数相除
原题目的要求是不能使用乘法, 除法和取余运算符实现除法.
在本篇博客中把题目要求提高一点, 这里只使用位运算来实现, 顺便的也就把只使用位运算实现加减乘除实现了.
1 . 实现加法
首先我们需要知道两数之和可以是两个数位相加和不进位相加之和, 而两数进行异或(^)运算其实就是两个数对应二进制值的无进位相加.
我们可以把思路可以转换一下, 把加法用异或替换, 如果我们能够得到两个数相加的二进制进位信息为0, 那么此时的无进位结果就是两数相加的最终结果了.
只有二进制无进位信息, 相加的结果; 然后把这个结果加上进位信息, 就是两个数相加的最终结果.
抽象一下:
我们要计算 a + b
先算 a ^ b = a' 得到的结果就是无进位相加的结果, 然后我们再得到 a 和 b 相加的进位信息 b’, 那么此时 a + b = a' + b' 就是两数之和, 但我们这里是不能用加号, 所以我们需要逐个把进位信息再继续叠加 (即让a’ 和 b’ 再继续运算, 得到进位信息和不进位信息…), 直到进位信息为 0 结束.
那么进位信息如何计算?
只有当 a 和 b 的二进制对应位置上都是1, 才会产生进位, 只需要 通过 (a & b) << 1 就可得到进位结果.
所以, 只使用位运算实现加法的代码如下:
// 不使用算数运算实现两数相加
public static int add (int a, int b) {
// 两个数的和等于两个数不进位相加和进位相加的和
// a ^ b 得到的就是两数不进位相加的和
// (a & b) << 1 得到的就是两数只相加进位的值
// 一直循环至进位值为0计算结束
int sum = a;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
}
return sum;
}
2 . 实现减法
两数相减, 等价于一个数加上另一个数的相反数, 即 a - b = a + (-b), 但这里是不能不能出现减号的, 所以, 可以用加法来模拟一个数的相反数, 因为 x 的相反数等于 x 取反再加 1 (~x + 1), 即 add(~x, 1).
所以, 只使用位运算实现减法可以在加法代码的基础上进行:
// 计算一个数字的相反数
public static int oppNum (int num) {
return add(~num, 1);
}
// 不使用算数运算实现两数相减
public static int minus(int a, int b) {
// a - b 就相当于 a + (-b)
// 一个数的相反数等于这个数取反再加1
return add(a, oppNum(b));
}
3 . 实现乘法
看下面计算两个十进制数的乘法用的方法是不是很熟悉, 以 a = 12, b = 22 为例, a * b 通过如下方式计算;
19
x 22
------
38
38
------
418
这样的方法也适用于二进制, 19 的二进制是 10011, 22 的二进制是 10110, 计算过程如下;
10011
x 10110
-------------
00000
10011
10011
00000
10011
------------
110100010
得到的计算结果 110100010 就是 418.
其实这里的二进制计算就对应着这样一个过程, 要求 a * b 的结果, 就从右往左开始遍历 b 的每一位二进制值, 如果 b 的第 i 位是 1, 则把 a 左移 i 位的累值加到结果中; 如果 b 的第 i 位是 0, 不需要处理, 最后累加完的结果就是 a * b 的答案.
只使用位运算实现乘法的代码如下:
// 不使用算数运算实现两数相乘
public static int mulit (int a, int b) {
// 就小学手算十进制类似
// 让 a 的每一位去乘 b 的每一位
int res = 0;
while (b != 0) {
if ((b & 1) != 0) {
res = add(res, a);
}
a <<= 1;
// 要注意 b 必须是无符号右移
b >>>= 1;
}
return res;
}
4 . 实现除法
在实现除法的时候, 为了防止溢出, 我们可以先把两数转换成正数来进行计算; 最后在计算末尾再判断两个数的符号决定是否把由正数计算出来的结果取其相反数.
假设 a / b = c, 则 a = b * c, 使用位运算就需要结合二进制来思考, 这里假设:
a = b * (2^7) + b * (2^4) + b * (2^1), 则 c 的二进制一定是10010010.
抽象一下, 如果a = b * (2 ^ m1) + b * (2 ^ m2) + b * (2 ^ m3), 则 c 的 m1 位置, m2 位置, m3 位置一定是 1, 其他位置都是 0.
所以, 我们实现除法的思路可以转换成 a 是由几个 ( b * 2 的某次方) 的结果组成.
所以, 只使用位运算实现除法的核心代码如下:
// 判断是不是负数
public static boolean isNegavit(int num) {
return num < 0;
}
// 这个适用于a和b都不是系统最小值的情况下
public static int div(int a, int b) {
// 这里的除法一定要保证两个数都是正数, 如果有负数在计算逻辑最后加上即可
int x = isNegavit(a) ? oppNum(a) : a;
int y = isNegavit(b) ? oppNum(b) : b;
int res = 0;
// 计算的是 x / y
// 每次循环 y 向左移动到和 x 最接近的值, 但要满足 y <= x, 如果是这个条件下, 也就是让 y 左移, 可能会溢出到符号位, 就可能会出错
// 实际上将 x 向右移动到和 y 最接近的值, 移动的位数和上面也是一样的, 不过要满足 x >= y;
for (int i = 30; i >= 0; i = minus(i, 1)) {
if ((x >> i) >= y) {
// 这个比特位一定是1
res |= (1 << i);
// x 减去 y << i;
x = minus(x, y << i);
}
}
// isNegavit(a) != isNegavit(b) 这个也可以用 isNegavit(a) ^ isNegavit(b) 来实现效果
return isNegavit(a) != isNegavit(b) ? oppNum(res) : res;
}
其中
if ((x >> i) >= y) {
// 这个比特位一定是1
res |= (1 << i);
// x 减去 y << i;
x = minus(x, y << i);
}
就是让 a 不断尝试其值是否由 (b * 2的某个次方) 相加得到.
但只有上面的实现还不够, 这里是有一些特殊情况需要考虑的, 比如在 Java 中, int 类型的系统最小值Integer.MIN_VALUE取相反数的结果依然是Integer.MIN_VALUE.
所以, 除法的两个操作数如果有系统最小值的话需要单独的进行计算处理.
- 如果两操作数都是系统最小值, 结果就是
1; - 如果只有除数 (b) 为系统最小值, 结果就是
0; - 如果被除数 (a) 为系统最小值, 除数为
-1时, 根据 LeetCode 题目要求, 结果就是Integer.MIN_VALUE / (-1) == Integer.MAX_VALUE; - 如果被除数 (a) 为系统最小值, 除数为
-1和Integer.MIN_VALUE时 (即a = Integer.MIN_VALUE且b != -1 && b != Integer.MIN_VALUE),a / b应该通过如下方式来计算;
- 可以先让先让系统最小值 +1 (
a + 1), 此时就可以按照正常上面的正常流程去计算除法了, 即(a + 1) / b = c. - 接着计算
a - (b * c) = d, 得到由于a + 1少/多算的. - 然后
d / b = e - 最后将
c和e相加就得到了 a / b 的值,c + e = ((a + 1)/b) + ((a - (b * c)) / b) = a / b
除了这些特殊, 就是正常的流程了, 所以, 加上针对系统最小值的特殊判断的代码如下:
// 除法的计算如果有系统最小值需要进行特殊判断(因为Integer.MAX_VALUE取反再+1得到的还是原来值), 也就是没办法计算相反数
public static int divide(int a, int b) {
if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
// 如果两数都是系统最小值
return 1;
} else if (b == Integer.MIN_VALUE){
// 如果除数为系统最小值
return 0;
} else if (a == Integer.MIN_VALUE) {
// 被除数为系统最小值
// 且除数为-1
if (b == oppNum(1)) {
// 答案应该是 Integer.MAX_VALUE + 1 的这个值的, 但力扣系统返回 Integer.MAX_VALUE 就行了
return Integer.MAX_VALUE;
} else {
// 系统最小值没法取相反数计算
// 1. c = (Integer.MAX_VALUE + 1) / b , 先让系统最小值 +1 后再除以 b
// 2. (Integer.MAX_VALUE - c * b) / b
// 3. 再将 1 和 2 的结果相加节课
int c = div(add(a, 1), b);
return add(c, div(minus(a, mulit(c, b)), b));
}
} else {
// 两数都不是系统最小值
return div(a, b);
}
}
完整实现的代码如下:
class Solution {
// 不使用算数运算实现两数相加
public static int add (int a, int b) {
// 两个数的和等于两个数不进位相加和进位相加的和
// a ^ b 得到的就是两数不进位相加的和
// (a & b) << 1 得到的就是两数只相加进位的值
// 一直循环至进位值为0计算结束
int sum = a;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
}
return sum;
}
// 计算一个数字的相反数
public static int oppNum (int num) {
return add(~num, 1);
}
// 不使用算数运算实现两数相减
public static int minus(int a, int b) {
// a - b 就相当于 a + (-b)
// 一个数的相反数等于这个数取反再加1
return add(a, oppNum(b));
}
// 不使用算数运算实现两数相乘
public static int mulit (int a, int b) {
// 就和小学手算十进制类似
// 让 a 的每一位去乘 b 的每一位
int res = 0;
while (b != 0) {
if ((b & 1) != 0) {
res = add(res, a);
}
a <<= 1;
// 要注意 b 必须是无符号右移
b >>>= 1;
}
return res;
}
// 不使用算数运算实现除法
// 判断是不是负数
public static boolean isNegavit(int num) {
return num < 0;
}
// 这个适用于a和b都不是系统最小值的情况下
public static int div(int a, int b) {
// 这里的除法一定要保证两个数都是正数, 如果有负数在计算逻辑最后加上即可
int x = isNegavit(a) ? oppNum(a) : a;
int y = isNegavit(b) ? oppNum(b) : b;
int res = 0;
// 计算的是 x / y
// 每次循环 y 向左移动到和 x 最接近的值, 但要满足 y <= x, 如果是这个条件下, 也就是让 y 左移, 可能会溢出到符号位, 就可能会出错
// 实际上将 x 向右移动到和 y 最接近的值, 移动的位数和上面也是一样的, 不过要满足 x >= y;
for (int i = 30; i >= 0; i = minus(i, 1)) {
if ((x >> i) >= y) {
// 这个比特位一定是1
res |= (1 << i);
// x 减去 y << i;
x = minus(x, y << i);
}
}
// isNegavit(a) != isNegavit(b) 这个也可以用 isNegavit(a) ^ isNegavit(b) 来实现效果
return isNegavit(a) != isNegavit(b) ? oppNum(res) : res;
}
// 除法的计算如果有系统最小值需要进行特殊判断(因为Integer.MAX_VALUE取反再+1得到的还是原来值), 也就是没办法计算相反数
public static int divide(int a, int b) {
if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
// 如果两数都是系统最小值
return 1;
} else if (b == Integer.MIN_VALUE){
// 如果除数为系统最小值
return 0;
} else if (a == Integer.MIN_VALUE) {
// 被除数为系统最小值
// 且除数为-1
if (b == oppNum(1)) {
// 答案应该是 Integer.MAX_VALUE + 1 的这个值的, 但力扣系统返回 Integer.MAX_VALUE 就行了
return Integer.MAX_VALUE;
} else {
// 系统最小值没法取相反数计算
// 1. c = (Integer.MAX_VALUE + 1) / b , 先让系统最小值 +1 后再除以 b
// 2. (Integer.MAX_VALUE - c * b) / b
// 3. 再将 1 和 2 的结果相加节课
int c = div(add(a, 1), b);
return add(c, div(minus(a, mulit(c, b)), b));
}
} else {
// 两数都不是系统最小值
return div(a, b);
}
}
}
当然, 按照原本的题意, 只是不能使用乘法, 除法和取余运算, 其他可以正常使用, 代码就简单了不少, 思路是一样的, 代码实现如下:
class Solution29 {
public static boolean isNegavit(int num) {
return num < 0;
}
public static int oppNum (int num) {
return (~num) + 1;
}
public static int mulit (int a, int b) {
// 就和小学手算十进制类似
// 让 a 的每一位去乘 b 的每一位
int res = 0;
while (b != 0) {
if ((b & 1) != 0) {
res += a;
}
a <<= 1;
// 要注意 b 必须是无符号右移
b >>>= 1;
}
return res;
}
public static int div(int a, int b) {
// 这里的除法一定要保证两个数都是正数, 如果有负数在计算逻辑最后加上即可
int x = isNegavit(a) ? oppNum(a) : a;
int y = isNegavit(b) ? oppNum(b) : b;
int res = 0;
// 计算的是 x / y
// 每次循环 y 向左移动到和 x 最接近的值, 但要满足 y <= x, 如果是这个条件下, 也就是让 y 左移, 可能会溢出到符号位, 就可能会出错
// 实际上将 x 向右移动到和 y 最接近的值, 移动的位数和上面也是一样的, 不过要满足 x >= y;
for (int i = 30; i >= 0; i--) {
if ((x >> i) >= y) {
// 这个比特位一定是1
res |= (1 << i);
// x 减去 y << i;
x -= (y << i);
}
}
// isNegavit(a) != isNegavit(b) 这个也可以用 isNegavit(a) ^ isNegavit(b) 来实现效果
return isNegavit(a) != isNegavit(b) ? oppNum(res) : res;
}
// 除法的计算如果有系统最小值需要进行特殊判断(因为Integer.MAX_VALUE取反再+1得到的还是原来值), 也就是没办法计算相反数
public static int divide(int a, int b) {
if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) {
// 如果两数都是系统最小值
return 1;
} else if (b == Integer.MIN_VALUE) {
// 如果除数为系统最小值
return 0;
} else if (a == Integer.MIN_VALUE) {
// 被除数为系统最小值
// 且除数为-1
if (b == -1) {
// 答案应该是 Integer.MAX_VALUE + 1 的这个值的, 但力扣系统返回 Integer.MAX_VALUE 就行了
return Integer.MAX_VALUE;
} else {
// 系统最小值没法取相反数计算
// 1. c = (Integer.MAX_VALUE + 1) / b , 先让系统最小值 +1 后再除以 b
// 2. (Integer.MAX_VALUE - c * b) / b
// 3. 再将 1 和 2 的结果相加节课
int c = div(a + 1, b);
return c + ((a - mulit(c, b)) / b);
}
} else {
// 两数都不是系统最小值
return div(a, b);
}
}
}
上述代码都是可以通过OJ的