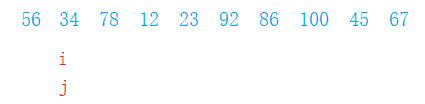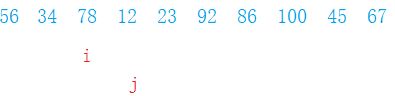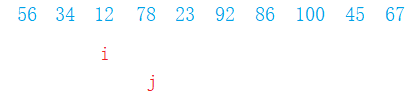快速排序—非递归、链表

                          快速排序—非递归、链表

对于快速排序相信大家都非常的清楚，对于越有序的数据，时间复杂度就越大。对于快排，时间复杂度为O(nlogn)，空间复杂度为O(nlogn)，是一种不稳定的排序算法。

对于递归的实现方法，在上篇博客中有，我们在这就不做介绍，我们就看一下，当我们的数据越有序的时候，时间复杂度就会越高，那怎么办呢，我们就可以采取以下的几种方式：

随机取值法：随机取一个值作为基准，进行划分

            srand(time(NULL));

            int pos = rand() % (right - left + 1) + left;

            swap(ar[pos], ar[left]);

            Partition(ar, left, right);

三位取中法：找到中间值，如何让他作为基准，进行划分：

            int mid = (right - left + 1)/2 + left;

             Partition(ar, left, right);

 

 

接下来，我们来实现非递归的形式。

1：我们使用一个栈来模拟递归，将他的左右下标放进去。代码如下：

template
void SNiceQuickPass(Type *ar, int left, int right)
{
	queue st;
	st.push(left);
	st.push(right);
	while (!st.empty())
	{

		left = st.front();
		st.pop();
		right = st.front();
		st.pop();
		int mid = Partition(ar,left ,right );
		if (left < mid - 1)
		{
			st.push(left);
			st.push(mid - 1);
		}
		if (mid + 1 < right)
		{
			st.push(mid+1);
			st.push(right);
		}
	}
}

2：既然栈是可以的，我们也可以使用队列来进行模拟，大同小异，注意进出顺序。

3：我们也可以使用STL下的 pair，就可以实现。

 

这个非递归是很容易理解的，接下来我们如果要将一个单链表，进行快排，我们应该怎样去解决呢？（单向划分）

我们定义两个下标，两个都是是当前下标的下一个下标。

以下列的规则进行变换：

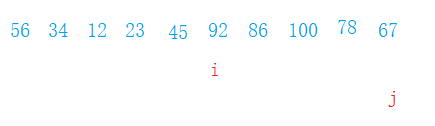
1. 如果下标j的值小于等于最左边的值，那么就让i和j的值交换，i、j ++；
2. 如果j大于最左边的值，那么j++；
3. 结束条件就是j大于最右边的下标就结束；
4. 最后i-1和最右边交换就完成了一次划分；

 

template
int OnePartition(Type *ar, int left, int right)
{
	int i = left+1 , j = i;
	while (j <= right)
	{
		if (ar[j] <= ar[left])
		{
			swap(ar[j], ar[i]);
			++j;
			++i;
		}
		else
		{
			++j;
		}
	}
	i = i - 1;
	swap(ar[left], ar[i]);
	return i;
}

 

这就是 单向划分的过程。在数组中很容易实现，但是我们看一下，我们的这个方法要完成单链表的快排，在单链表中怎样进行i=i-1呢，这时候我们就应该这样的处理我们的i和j；

 

struct Node * ListPartition(struct Node *begin, struct Node *end)
{
	struct Node *i = begin, *j = i->next;
	while (j != end)
	{
		if (j->data <= begin->data)
		{
			swap(i->next->data, j->data);
			i = i->next;
			j = j->next;
		}
		else
			j = j->next;
	}
	swap(begin->data, i->data);
	return i;
}