加减乘除求余 利用 位运算实现(详细)
用位运算实现除法和求余运算?这一下子把不了解二进制的小白搞蒙了。
因此,查阅许多资料,写出用位运算实现的加减乘除以及求余的代码,附详细思路,权当笔记,也分享给大家。
首先,我们得了解位运算符:
| 符号 |
描述 |
运算规则 |
| & |
与 |
两个位都为1时,结果才为1 |
| | |
或 |
两个位都为0时,结果才为0 |
| ^ |
异或 |
两个位相同为0,相异为1 |
| ~ |
取反 |
0变1,1变0 |
| << |
左移 |
各二进位全部左移若干位,高位丢弃,低位补0 |
| >> |
右移 |
各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移) |
(1) 首先是&,按位与运算符,两个位都为1时,结果才为1。
例:
2 & 3 ==> 0000 0010 & 0000 0011 = 0000 0010 即2 & 3 = 2
可见,对于十进制转换成的二进制数,按照相应位的比对而得出结果。
(2)其次是 | ,按位或运算符,两个位都为0时,结果才为0,
例:
2 & 3 ==> 0000 0010 | 0000 0011 = 0000 0011 即2 | 3 = 3
(3)按位异或运算符^,两个位相同为0,相异为1。
例:
2 ^ 3 ==> 0000 0010 ^ 0000 0011 = 0000 0001 即2 ^ 3 = 1
(4)取反~,很好理解,0变1,1变成0.
例:
~3 即 0000 0011 ==> 1111 1100
(5)最后,按位左移 和 按位右移 的意思就是字面意思。
例:
3<<1 即 0000 0011 ==> 0000 0110
3<<2 即 0000 0011 ==> 0000 1100
好了,基础知识到位,开始理论研究!
加法
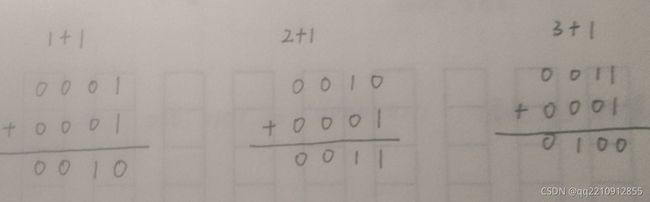
我们先从加法开始,先看一个二进制加法图:
研究1+1 可以看出,最低位满2进1,即1 和 1 => 0 (1^1=0)
然后前进一位加上1,即 0 和 0 => 1 (应由前一位的1&1=1来获得进位数,此时按位左移即进位)
研究2+1 可以看出,因为不需要进位,即 0 和 1 => 1
研究3+1 运用研究1+1 和 2+1的结论,可以发现只是前两者的嵌套。
因此,我们发现,1 和 1 的运算 ,同位变成0,上一位由0变1,或由1变0
,以1+1为例,得到:
最后,代码实现:
int Add(int a,int b)//加法位运算a+b
{
if(b)
{
return Add(a ^ b, (a & b) << 1);
}
else
{
return a;
}
}
减法
很容易想到,减法就是加上一个数的负数
而二进制负数如何得来?这里转载一些资料:
在二进制里,最高位为符号位,用0和1 来表示正负,最高位为 1 代表负数,最高位为 0 代表正数。
负数的二进制表示分为三步:
1 把这个负数的绝对值转换为二进制,即求原码
2 把原码取反,即求反码
3 把反码加1,即求补码
例如把 -5 转换为二进制,假设-5为Java中的byte类型。
bytei=5;
1 求原码:即把-5的绝对值5转换为二进制 为 00000101
2 求反码:为 11111010
3 求补码:为 11111011
来自 <计算机基础知识 | 负数的二进制表示 - 知乎>
因此,代码只需要将减数求反以及补码即可
int Subt(int a, int b)//减法位运算a-b
{
return Add(a, Add(~b, 1));
}乘法
按照小学的理解,其实就是被乘数进行乘数次的累加而已:
如:3*3 就是3+3+3
代码实现:
int Multi(int a, int b)//乘法位运算a*b
{
int i,sum=0;
for (i=b;i>0;i--)
{
sum=Add(sum,a);
}
return sum;
}
后面转载乘法的另一种思路:
一开始考虑到乘法其实是加法的延续,是一种累加运算,只要将被乘数进行乘数次相加即可,但这样的做法存在一个很明显的问题即当乘数很大时需要进行多次加法运算。下面介绍一种改进的乘法思路,这种思路由手作乘法的过程的方法而来。在进行手动乘法时,我们根据乘数的尾数是否为1来确定是否需要相加。即若乘数的尾数是1,那么就要加上被乘数,否则则不需要加上被乘数。在本次判断之后,我们需要将被乘数左移一位,乘数逻辑右移一位。整个过程在乘数为0时停止。
同时需要注意符号的问题,这里我们首先进行绝对值的运算,再通过a^b是否小于0判断符号的异同性。
int Multiply(int a, int b){
int a1 = a > 0 ? a : Add(~a, 1);
int b1 = b > 0 ? b : Add(~b, 1);
int sum = 0;
while(b1){
if(b1 & 0x1){
sum = Add(sum, a1);
}
a1 = a1 << 1;
b1 = b1 >> 1;
}
if((a ^ b) < 0)
return Add(~sum, 1);
else return sum;
}
转自 位运算实现加减乘除运算——超详细C语言描述_Pe_99y的博客-CSDN博客
除法
除法同理,即是乘法的逆运算,重复减除数,知道被除数小于除数
代码实现:
int Divide(int a,int b)
{
int i=0;
while(a下面再转载另一种思路的文章:
跟加法、减法一样,除法是乘法的逆运算,那么除法就是做有限次的减法,直到被减数小于减数为止。这种思路类似于乘法中的简单思路,问题同样是在被除数远大于除数时,需要做多次除法。
改良的除法思路如下,考虑到int型整数占32位,那么用i = 31开始比较被除数与除数的2i的大小,若被除数大,则在商处直接加上i从而减小减法的次数。
int Divide(int a, int b){
int quotient = 0;
if(!b){
cout << "Error" << endl;
return 1;
}
for(int i = 31; i --; i > 0){
if((a >> i) >= b)
{
quotient = Add(quotient, 1 << i);
a = Minus(a, b << i);
}
}
if((a ^ b) < 0)
quotient = Add(~quotient, 1);
return quotient;
}
原文链接:https://blog.csdn.net/qq_41716838/article/details/92193515
求余
求余即是用除法的结果乘上原除数,与被除数做差
代码实现:
int fish(int a,int b)//求余位运算a%b
{
int c,f;
c = Divide(a,b);
f = a - (Multiply(b,c));
return f;
}
最后,我们可以进行5种运算,做开始那道题更是毫无压力。
本文除了引用(以附原链接)均原创,谢谢大家支持和学习!