二叉树笔记 2023.2.28复习
目录
-
-
- 1 树的概念
- 2 分治算法
- 二分收索树(Binary Search Tree, BST):
-
- 判断是否是一颗二分搜索树 Is Binary Search Tree ?
- 判断是否是一颗二叉平衡树 Balanced Binary Tree
- 树2是否为树1的子树 Subtree
- 计算二叉树的深度Tree Depth
- Tree的Path问题
- 找出二叉树中,所有路径和为sum的路径 Path Sum
- 找出二叉树中,所有路径和(以叶子节点结尾)为sum的路径 Path Sum2
- 有序数组转为二叉搜索树 Sorted Array to Binary Search Tree
- 寻找特定节点
- 给定一个节点,找下一个节点 Find Next in Binary Tree
- 给定一个节点,找下一个节点 (没有指向父节点的指针)Find Next in Binary Search Tree
- 找两个节点的最近祖先Lowest Common Ancestor(LCA)
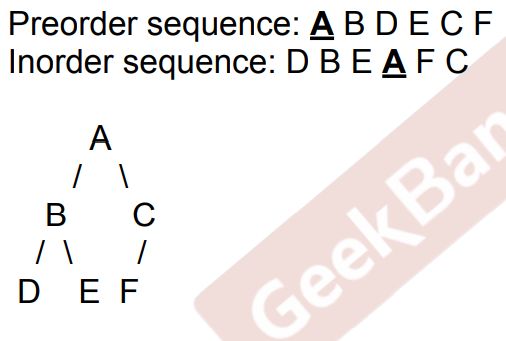
- 根据前序和中序遍历重建二叉树 Rebuild Binary Tree
- 二叉树的水平遍历 Binary Tree Level Order Traversal
- 打印k1,k2之间的二叉树节点 Print Range in a Binary Search Tree
- Trie Tree
-
1 树的概念
class TreeNode {
public:
TreeNode* left;
TreeNode* right;
//TreeNode* parent;
int val;
};
class BinaryTree {
public:
BinaryTree(int rootValue);
~BinaryTree();
bool insertNodeValue(int value);
bool deleteNodeWithValue(int value);
void printTree();
private:
TreeNode* root;
};
-
前序遍历: [ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
-
中序遍历: [ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
-
后序遍历: [ [左子树的后序遍历结果], [右子树的后序遍历结果] ,根节点]
递归实现
void visit(TreeNode* root){
cout << root->val << endl;
}
void preOrderTraversal(TreeNode* root) {
if (!root) {
return;
}
visit(root);
preOrderTraversal(root->left);
preOrderTraversal(root->right);
}
void inOrderTraversal(TreeNode* root) {
if (!root) {
return;
}
inOrderTraversal(root->left);
visit(root);
inOrderTraversal(root->right);
}
void postOrderTraversal(TreeNode* root) {
if (!root) {
return;
}
postOrderTraversal(root->left);
postOrderTraversal(root->right);
visit(root);
}
⾮递归实现
vector<int> preOrderTraversal(TreeNode* root, vector<int>& result) {
if (root == NULL) return result;
stack<TreeNode* > sta;
sta.push(root);
while (!sta.empty()) {
TreeNode* node = sta.top();
sta.pop();
result.push_back(node->val);
//先进后出,先放右边
if (root->right!=NULL)
sta.push(root->right);
if (root->left!=NULL)
sta.push(root->left);
}
return result;
}
水平遍历
BFS
void levelTraversal(TreeNode* root) {
queue <TreeNode*> nodeQueue;
if (root==NULL) {
return;
}
nodeQueue.push(root);
while (!nodeQueue.empty())
{
TreeNode* temp = nodeQueue.front();
nodeQueue.pop();
visit(temp);
if (temp->left != NULL)
nodeQueue.push(temp->left);
if (temp->right != NULL)
nodeQueue.push(temp->right);
}
}
2 分治算法
⼆分搜索、 ⼤整数乘法、 归并排序、 快速排序
二分收索树(Binary Search Tree, BST):
O(logn)~O(n)
判断方法:
- 中序遍历是不是增序的
- 可以同时传⼊最⼩/最⼤值,并且将初始值设为INT_MIN,INT_MAX,这样,其左⼦树所有节点的值必须在 INT_MIN及根节点的值之间,其右⼦树所有节点的值必须在根节点的值以及INT_MAX之间。
判断是否是一颗二分搜索树 Is Binary Search Tree ?
bool helper(TreeNode* root, int min, int max) {
if (root!=NULL)return true;
//如果有元素INT_MAX,必须在最右边
//如果有元素INT_MIN,必须在最左边
if ((root->val < max || (root->val == INT_MAX && root->right == NULL))
&& (root->val > min || (root->val == INT_MIN && root->left== NULL))
&& helper(root->left, min, root->val)
&& helper(root->right, root->val, max)
)
return true;
return false;
}
bool isValidBST(TreeNode* root) {
return helper(root, INT_MAX, INT_MIN);
}
判断是否是一颗二叉平衡树 Balanced Binary Tree
⼀颗⼆叉树(Balanced Binary Tree)是平衡的,当且仅当左右两个⼦树的⾼度差的绝对值不超过 1,并且左右两个⼦树都是⼀棵平衡⼆叉树。
Is Balanced Binary Tree ?
int level(TreeNode* root) {
if (root == NULL) return 0;
return max(level(root->left), level(root->right)) + 1;
}
bool isBalanced(TreeNode* root) {
if (root == NULL)
return true;
int factor = abs(level(root->left) - level(root->right));
return factor <= 1 && isBalanced(root->right) && isBalanced(root->left);
}
更好的实现?
⼀种改进⽅式是,可以考虑利⽤动态规划的思想,将TreeNode指针作为key,⾼度作为value,⼀旦发现节点已经被计算过,直接返回结果,这样,level函数对每个节点只计算⼀次。
另⼀种更为巧妙的⽅法是,isBalanced返回当前节点的⾼度,⽤-1表⽰树不平衡。 将计算结果⾃底向上地传递,并且确保每个节点只被计算⼀次,复杂度O(n)。
//isBalanced返回当前节点的⾼度,返回-1代表树不平衡
int isBalanceHelper(TreeNode* root) {
if (root == NULL)return 0;
int leftHeight = isBalanceHelper(root->left);
if (leftHeight == -1)return -1;
int rightHeight = isBalanceHelper(root->right);
if (rightHeight == -1)return -1;
if (abs(leftHeight - rightHeight) > 1)return -1;
return max(leftHeight, rightHeight)+1;
}
bool isBalanceTree(TreeNode* root) {
return isBalanceTree(root) != -1;
}
树2是否为树1的子树 Subtree
Tree1 and Tree2 are both binary trees nodes having value, determine if Tree2 is a subtree of Tree1.
//matchtree:判断以root1和root2为根节点的两个树是否相等
bool matchTree(TreeNode* root1, TreeNode* root2) {
if (root1 == NULL && root2 == NULL)return true;
if (root1 == NULL || root2 == NULL)return false;
if (root1->val != root2->val)return false;
return matchTree(root1->left, root2->left) && matchTree(root1->right , root2->right);
}
//tree1当前节点和tree2的root相等的时候,调用matchtree ; 不相等时,递归:当前节点的左子树和由指数是否包含tree2_root
bool subTree(TreeNode *root1,TreeNode *root2) {
if (root2 == NULL)return true;
if (root1 == NULL)return false;
if (root1->val == root2->val)return matchTree(root1, root2);
return subTree(root1->left, root2) || subTree(root1->right, root2);
}
计算二叉树的深度Tree Depth
Compute the depth of a binary tree
int treeDepth(TreeNode* node) {
if (node == NULL)return 0;
return max(treeDepth(node->left), treeDepth(node->right)) + 1;
}
Tree的Path问题
找出⼀条满⾜特定条件的路径 。对于这类问题,通常都是传⼊⼀个vector记录当 前⾛过的路径(为尽可能模版化,统⼀记为path), 还需要传⼊另⼀个vector引⽤记录所有符合条件的path(为尽可能模版化,统⼀记 为result)。
注意, result可以⽤引⽤或指针形式,相当于⼀个全局变量,或者就开辟⼀个独⽴于函数的成员变量。由于path通常是vector ,那么result就是 vector
找出二叉树中,所有路径和为sum的路径 Path Sum
Get all the paths (always starts from the root) in a binary tree, whose sum would be equal to given value.
//从根节点开始,遍历左右子树,path记录所有的路径,result记录符合条件的路径
void pathSumHelper(vector<int> path, vector<vector<int>>& ans, TreeNode* root, int sum) {
if (root == NULL)return;
path.push_back(root->val);
if (root->val == sum)ans.push_back(path);
pathSumHelper(path,ans,root->right,sum-root->val);
pathSumHelper(path, ans, root->left, sum - root->val);
}
找出二叉树中,所有路径和(以叶子节点结尾)为sum的路径 Path Sum2
Get all the paths (always starts from the root and ends at leaf) in a binary tree, whose sum would be equal to given value.
void pathSumHelper(vector<int> path, vector<vector<int>>& ans, TreeNode* root, int sum) {
if (root == NULL)return;
path.push_back(root->val);
if (root->val == sum && root->left ==NULL && root->right == NULL)ans.push_back(path);//区别sum1加了叶子结点的条件
pathSumHelper(path,ans,root->right,sum-root->val);
pathSumHelper(path, ans, root->left, sum - root->val);
}
有序数组转为二叉搜索树 Sorted Array to Binary Search Tree
TreeNode* helper(vector<int>num, int first, int last) {
if (first == last) {
TreeNode* root = new TreeNode(num[first]);
return root;
}
if (first > last) {
return NULL;
}
int mid = (first + last) / 2;
TreeNode* root = new TreeNode(num[mid]);
root->left = helper(num, first, mid - 1);
root->right = helper(num, mid + 1, last);
return root;
}
TreeNode* sortedArray2BTS(vector<int> num) {
if (num.size() == 0)return NULL;
if (num.size() == 1) {
TreeNode* root = new TreeNode(num[0]);
return root;
}
int first = 0, last = num.size() - 1;
return helper(num, first, last);
}
寻找特定节点
此类题⽬通常会传入一个当前节点,要求找到与此节点具有⼀一定关系的 特定节点:例如前驱,后继,左/右兄弟等。
了解一下常见特定节点的定义及性质。
在存在指向父节点指针的情况下, 通常可以由当前节点出发,向上倒推解决。
如果节点没有父节点指针,一般需要从根节点出发向下搜索,搜索的过程就是DFS。
给定一个节点,找下一个节点 Find Next in Binary Tree
给定一棵树,给定一个节点,寻找指定节点在中序遍历中的下一个节点。
例子:
中序遍历:4 8 10 12 14 20 22
给定14,找出20
In-order traverse a binary tree with parent links, find the next node to visit given a specific node.
思路:
该节点有无右子树:
有,找到右子树的最左孩子;
无,找到根,而且该根是左孩子,这个根的父节点为所求;
值得再写几遍!!!
//找最左的孩子
TreeNode* leftMostNode(TreeNode* node) {
if (node == NULL)return NULL;
if (node->left == NULL)return node;
return leftMostNode(node->left);
}
//判断node是不是root的左孩子
bool isLeftchild(TreeNode* node, TreeNode* root) {
return (root->left==node);
}
TreeNode* inOrderSuccessor(TreeNode* node) {
if (node == NULL)return NULL;
//不能这样写,叶子结点右子树为null,但中序遍历有下一个节点
//if (node->right == NULL)return NULL;
if(node->right) return leftMostNode(node->right);
//node->right为空,找到node对应的根节点
TreeNode* parent = node->parent;
//while这里相当于递归
while (parent&& !isLeftchild(node,parent)) {
node = parent;
parent = parent->parent;
}
return parent;
}
给定一个节点,找下一个节点 (没有指向父节点的指针)Find Next in Binary Search Tree
In-order traverse a binary search tree with parent links, find the next node to visit given a specific node
condition: without parent link
思路:
该节点有无右子树:
有,找到右子树的最左孩子;
无,找到根,遍历根的左子树,找到大于node的最小点为所求;
值得再写几遍!!!
//找最左的孩子
TreeNode* leftMostNode(TreeNode* node) {
if (node == NULL)return NULL;
if (node->left == NULL)return node;
return leftMostNode(node->left);
}
//要找比当前节点大的所有的最小的那个
TreeNode* inOrderSuccessor(TreeNode* node,TreeNode* root) {
if (root == NULL)return NULL;
if (node->right)return leftMostNode(node->right);
TreeNode* ans = NULL;
//根节点大于当前节点的条件下, 存储当前节点为答案
while (root){
if (root->val > node->val) {
ans = root;
root = root->left;
}
else {
root = root->right;
}
}
return ans;
}
找两个节点的最近祖先Lowest Common Ancestor(LCA)
Given a binary tree and two nodes. Find the lowest common ancestor of the two nodes in the tree
法1:
//构建辅助函数:确定节点是不是在某节点的子树中
bool cover(TreeNode* root, TreeNode* node) {
if (root->val == NULL)return false;
if (root->val == node->val)return true;
return (cover(root->left, node) || cover(root->right, node));
}
//如果两个节点都在该子树的左子树中,解一定在该节点的左子树中
//如果两个节点都在该子树的右子树中,解一定在该节点的右子树中
//如果两个节点在该子树的一左一右中,解就是该节点
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* A, TreeNode* B) {
if (root == NULL) return NULL;
if (cover(root->left, A) && cover(root->left, B))
return lowestCommonAncestor(root->left, A, B);
if (cover(root->right, A) && cover(root->right, B))
return lowestCommonAncestor(root->right, A, B);
return root;
}
根据前序和中序遍历重建二叉树 Rebuild Binary Tree
Pre-order + In-order
private:
unordered_map<int, int> index;
public:
TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return nullptr;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = index[preorder[preorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
// 构造哈希映射,帮助我们快速定位根节点
for (int i = 0; i < n; ++i) {
index[inorder[i]] = i;
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
二叉树的水平遍历 Binary Tree Level Order Traversal
void printLevelZigZag(TreeNode* root) {
//用栈原因:z型输出
stack<TreeNode*> currentLevel, nextLevel;
bool left2right = true;
currentLevel.push(root);
while (!currentLevel.empty()) {
TreeNode* currNode = currentLevel.top();
currentLevel.pop();
if (currNode) {
cout << currNode->val << " ";
if (left2right) {
nextLevel.push(currNode->left);
nextLevel.push(currNode->right);
}
else {
nextLevel.push(currNode->right);
nextLevel.push(currNode->left);
}
}
if (currentLevel.empty()) {
cout << endl;
left2right = !left2right;
swap(currentLevel, nextLevel);
}
}
}
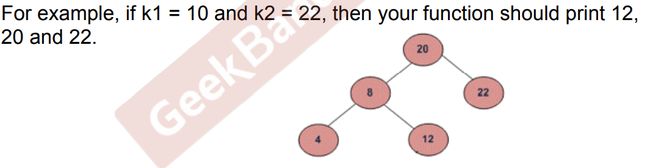
打印k1,k2之间的二叉树节点 Print Range in a Binary Search Tree
Given two values k1 and k2 (where k1 < k2) and a root pointer to a Binary Search Tree. Print all the keys of tree in range k1 to k2. i.e. print all x such that k1<=x<=k2 and x is a key of given BST. Print all the keys in increasing order.
//k1
void Print(TreeNode* root, int k1, int k2) {
if (root == NULL)return ;
//k1在根节点的左侧,一定要打印左子树
if (k1 < root->val)Print(root->left, k1, k2);
if (k1<root->val && k2>root->val)cout << root->val << endl;
//k2在根节点的右侧,一定要打印右子树
if (k2 > root->val)Print(root->right, k1, k2);
}
Trie Tree
字典树(trie or prefix tree)是⼀个26叉树,⽤于在⼀个集合中检索⼀个字符串,或者字符串前缀。字典树的每个节点有⼀个指针数组代表其所有⼦树,其本质上是⼀个hash table,因为⼦树所在的位置(index)本⾝,就代表了节点对应的字母.
代码待补充ing