第 5 章 数组和广义表（稀疏矩阵的三元组顺序表存储实现）

1. 背景说明

为了节省存储空间，可以对这类矩阵进行压缩存储。所谓压缩存储是指：为多个值相同的元只分配一个存储空间，对零元不分配空间。

2. 示例代码

1)status.h

/* DataStructure 预定义常量和类型头文件 */
#include 

#ifndef STATUS_H
#define STATUS_H

#define NONE ""

#define FILE_NAME(X) strrchr(X, '\\') ? strrchr(X,'\\') + 1 : X

#define DEBUG

#define CHECK_NULL(pointer) if (!(pointer)) { \
	printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_NULL_PTR); \
	return NULL; \
}

#define CHECK_FALSE(value, ERR_CODE) if (!(value)) { \
	printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_CODE); \
	return FALSE; \
}

#ifdef DEBUG
#define CHECK_RET(ret, FORMAT, ...) if (ret != RET_OK) { \
		printf("FileName: %-20s FuncName: %-15s Line: %-5d ErrorCode: %-3d" FORMAT "\n", FILE_NAME(__FILE__), __func__, __LINE__, ret, ##__VA_ARGS__); \
		return ret; \
	}
#else
#define CHECK_RET(ret, FORMAT, ...)
#endif

#ifdef DEBUG
#define CHECK_VALUE(value, ERR_CODE, FORMAT, ...) if (value) { \
		printf("FileName: %-20s FuncName: %-15s Line: %-5d ErrorCode: %-3d" FORMAT "\n", FILE_NAME(__FILE__), __func__, __LINE__, ERR_CODE, ##__VA_ARGS__); \
		return ERR_CODE; \
	}
#else
#define CHECK_VALUE(value, ERR_CODE, FORMAT, ...)
#endif

/* 函数结果状态码 */
#define TRUE 					1			/* 返回值为真 */
#define FALSE 					0			/* 返回值为假 */
#define RET_OK 					0			/* 返回值正确 */
#define ERR_MEMORY     		   	2			/* 访问内存错 */
#define ERR_NULL_PTR   			3			/* 空指针错误 */
#define ERR_MEMORY_ALLOCATE		4			/* 内存分配错 */
#define ERR_NULL_STACK			5			/* 栈元素为空 */
#define ERR_PARA				6			/* 函数参数错 */
#define ERR_OPEN_FILE			7			/* 打开文件错 */
#define ERR_NULL_QUEUE			8			/* 队列为空错 */
#define ERR_FULL_QUEUE			9			/* 队列为满错 */
#define ERR_NOT_FOUND			10			/* 表项不存在 */
typedef int Status;							/* Status 是函数的类型,其值是函数结果状态代码，如 RET_OK 等 */
typedef int Bollean;						/* Boolean 是布尔类型,其值是 TRUE 或 FALSE */

#endif // !STATUS_H

2) tripleSparseMatrix.h

/* 稀疏矩阵的三元组顺序表存储表示头文件 */

#include "status.h"

#define MAX_SIZE 100

typedef int ElemType;

typedef struct {
	int i;
	int j;
	ElemType e;
} Triple;

typedef struct {
	Triple data[MAX_SIZE + 1];
	int rowNum;
	int colNum;
	int noneZeroNum;
} TSMatrix;

/* 创建稀疏矩阵 *sMatrix */
Status CreateSMatrix(TSMatrix *sMatrix);

/* 销毁稀疏矩阵 *sMatrix */
Status DestroySMatrix(TSMatrix *sMatrix);

/* 按照矩阵形式输出 *sMatrisx */
Status PrintSMatrix(const TSMatrix *sMatrix);

/* 由稀疏矩阵 *sMatrixA 复制得到 *sMatrixB */
Status CopySMatrix(const TSMatrix *sMatrixA, TSMatrix *sMatrixB);

/* 求稀疏矩阵 *sMatrixA 和 *sMatrixB 的和矩阵 *sMatrixC */
Status AddSMatrix(const TSMatrix *sMatrixA, const TSMatrix *sMatrixB, TSMatrix *sMatrixC);

/* 求稀疏矩阵 *sMatrixA 和 *sMatrixB 的差矩阵 *sMatrixC */
Status SubSMatrix(const TSMatrix *sMatrixA, TSMatrix *sMatrixB, TSMatrix *sMatrixC);

/* 算法 5.1，
   求稀疏矩阵 *sMatrix 的转置矩阵 *sMatrixT */
Status TransposeSMatrix(const TSMatrix *sMatrix, TSMatrix *sMatrixT);

/* 算法 5.2，
   快速求稀疏矩阵 *sMatrix 的转置矩阵 *sMatrixT */
Status FastTransposeSMatrix(const TSMatrix *sMatrix, TSMatrix *sMatrixT);

/* 求稀疏矩阵 *sMatrixA 和 *sMatrixB 的乘积矩阵 *sMatrixC */
Status MultSMatrix(const TSMatrix *sMatrixA, const TSMatrix *sMatrixB, TSMatrix *sMatrixC);

3) tripleSparseMatrix.c

/* 稀疏矩阵的三元组顺序表存储实现源文件 */

#include "tripleSparseMatrix.h"
#include 
#include 

/* 创建稀疏矩阵 *sMatrix */
Status CreateSMatrix(TSMatrix *sMatrix)
{
	CHECK_VALUE(!sMatrix, ERR_NULL_PTR, NONE);
	printf("Please input the row, col, noneZeroElement of the matrix: ");
	scanf_s("%d%d%d", &(sMatrix->rowNum), &(sMatrix->colNum), &(sMatrix->noneZeroNum));
	CHECK_VALUE((sMatrix->rowNum < 1) || (sMatrix->colNum < 1) || (sMatrix->noneZeroNum < 0)
		|| (sMatrix->noneZeroNum > (sMatrix->rowNum * sMatrix->colNum)) || (sMatrix->noneZeroNum > MAX_SIZE),
		ERR_PARA, "rowNum = %d, colNum = %d, noneZeroNum = %d", sMatrix->rowNum, sMatrix->colNum, sMatrix->noneZeroNum);
	sMatrix->data[0].i = 0;
	int row, col;
	ElemType e;
	int i;
	for (i = 1; i <= sMatrix->noneZeroNum; ++i) {
		printf("Please input the row(1 ~ %d), col(1 ~ %d), and the value of %dth element: ", sMatrix->rowNum,
			sMatrix->colNum, i);
		scanf_s("%d%d%d", &row, &col, &e);
		CHECK_VALUE((row < 1) || (row > sMatrix->rowNum) || (col < 1) || (col > sMatrix->colNum) ||
			(row < sMatrix->data[i - 1].i) || ((row == sMatrix->data[i - 1].i) && (col <= sMatrix->data[i - 1].j)),
			ERR_PARA, "row = %d, rowNum = %d, col = %d, colNum = %d, lastRow = %d, lastCol = %d", row, sMatrix->rowNum,
			col, sMatrix->colNum, sMatrix->data[i - 1].i, sMatrix->data[i - 1].j);
		sMatrix->data[i].i = row;
		sMatrix->data[i].j = col;
		sMatrix->data[i].e = e;
	}

	return RET_OK;
}

/* 销毁稀疏矩阵 *sMatrix */
Status DestroySMatrix(TSMatrix *sMatrix)
{
	CHECK_VALUE(!sMatrix, ERR_NULL_PTR, NONE);
	sMatrix->rowNum = sMatrix->colNum = sMatrix->noneZeroNum = 0;

	return RET_OK;
}

/* 按照矩阵形式输出 *sMatrisx */
Status PrintSMatrix(const TSMatrix *sMatrix)
{
	CHECK_VALUE(!sMatrix, ERR_NULL_PTR, NONE);
	int count = 1;
	for (int i = 1; i <= sMatrix->rowNum; ++i) {
		for (int j = 1; j <= sMatrix->colNum; ++j) {
			if ((count <= sMatrix->noneZeroNum) && (sMatrix->data[count].i == i) && (sMatrix->data[count].j == j)) {
				printf("%-3d", sMatrix->data[count].e);
				++count;
				continue;
			}

			printf("%-3d", 0);
		}

		printf("\n");
	}

	return RET_OK;
}

/* 由稀疏矩阵 *sMatrixA 复制得到 *sMatrixB */
Status CopySMatrix(const TSMatrix *sMatrixA, TSMatrix *sMatrixB)
{
	CHECK_VALUE(!sMatrixA || !sMatrixB, ERR_NULL_PTR, "sMatrixA = %p sMatrixB = %p", sMatrixA, sMatrixB);
	errno_t ret = memcpy_s(sMatrixB, sizeof(TSMatrix), sMatrixA, sizeof(TSMatrix));
	CHECK_RET(ret, NONE);

	return RET_OK;
}

/* 返回 num1 和 num2 的大小比较结果 */
int Compare(int num1, int num2)
{
	return (num1 < num2) ? -1 : ((num1 == num2) ? 0 : 1);
}

/* 求稀疏矩阵 *sMatrixA 和 *sMatrixB 的和矩阵 *sMatrixC */
Status AddSMatrix(const TSMatrix *sMatrixA, const TSMatrix *sMatrixB, TSMatrix *sMatrixC)
{
	CHECK_VALUE(!sMatrixA || !sMatrixB || !sMatrixC, ERR_NULL_PTR, "sMatrixA = %p, sMatrixB = %p, sMatrixC = %p",
		sMatrixA, sMatrixB, sMatrixC);
	CHECK_VALUE((sMatrixA->rowNum != sMatrixB->rowNum) || (sMatrixA->colNum != sMatrixB->colNum), ERR_PARA,
		"sMatrixA_rowNum = %d, sMatrixB_rowNum = %d, sMatrixA_colNum = %d, sMatrixB_colNum = %d", sMatrixA->rowNum,
		sMatrixB->rowNum, sMatrixA->colNum, sMatrixB->colNum);
	sMatrixC->rowNum = sMatrixA->rowNum;
	sMatrixC->colNum = sMatrixA->colNum;
	int noneZeroNumA = 1, noneZeroNumB = 1, noneZeroNumC = 0;
	errno_t ret;
	while ((noneZeroNumA <= sMatrixA->noneZeroNum) && (noneZeroNumB <= sMatrixB->noneZeroNum)) {
		switch (Compare(sMatrixA->data[noneZeroNumA].i, sMatrixB->data[noneZeroNumB].i)) {
		case -1:
			ret = memcpy_s(&(sMatrixC->data[++noneZeroNumC]), sizeof(Triple), &(sMatrixA->data[noneZeroNumA++]), sizeof(Triple));
			break;
		case 0:
			switch (Compare(sMatrixA->data[noneZeroNumA].j, sMatrixB->data[noneZeroNumB].j)) {
			case -1:
				ret = memcpy_s(&(sMatrixC->data[++noneZeroNumC]), sizeof(Triple), &(sMatrixA->data[noneZeroNumA++]), sizeof(Triple));
				break;
			case 0:
				ret = memcpy_s(&(sMatrixC->data[++noneZeroNumC]), sizeof(Triple), &(sMatrixA->data[noneZeroNumA++]), sizeof(Triple));
				sMatrixC->data[noneZeroNumC].e += sMatrixB->data[noneZeroNumB++].e;
				if (sMatrixC->data[noneZeroNumC].e == 0) {
					--noneZeroNumC;
				}
				break;
			case 1:
				ret = memcpy_s(&(sMatrixC->data[++noneZeroNumC]), sizeof(Triple), &(sMatrixB->data[noneZeroNumB++]), sizeof(Triple));
				break;
			}

			break;
		case 1:
			ret = memcpy_s(&(sMatrixC->data[++noneZeroNumC]), sizeof(Triple), &(sMatrixB->data[noneZeroNumB++]), sizeof(Triple));
			break;
		}

		CHECK_RET(ret, NONE);
	}

	while (noneZeroNumA <= sMatrixA->noneZeroNum) {
		ret |= memcpy_s(&(sMatrixC->data[++noneZeroNumC]), sizeof(Triple), &(sMatrixA->data[noneZeroNumA++]), sizeof(Triple));
	}

	while (noneZeroNumB <= sMatrixB->noneZeroNum) {
		ret |= memcpy_s(&(sMatrixC->data[++noneZeroNumC]), sizeof(Triple), &(sMatrixB->data[noneZeroNumB++]), sizeof(Triple));
	}

	CHECK_RET(ret, NONE);
	sMatrixC->noneZeroNum = noneZeroNumC;
	CHECK_VALUE(noneZeroNumC > MAX_SIZE, ERR_PARA, "noneZeroNumC = %d", noneZeroNumC);

	return RET_OK;
}

/* 求稀疏矩阵 *sMatrixA 和 *sMatrixB 的差矩阵 *sMatrixC */
Status SubSMatrix(const TSMatrix *sMatrixA, TSMatrix *sMatrixB, TSMatrix *sMatrixC)
{
	CHECK_VALUE(!sMatrixA || !sMatrixB || !sMatrixC, ERR_NULL_PTR, "sMatrixA = %p, sMatrixB = %p, sMatrixC = %p",
		sMatrixA, sMatrixB, sMatrixC);
	CHECK_VALUE((sMatrixA->rowNum != sMatrixB->rowNum) || (sMatrixA->colNum != sMatrixB->colNum), ERR_PARA,
		"sMatrixA_rowNum = %d, sMatrixB_rowNum = %d, sMatrixA_colNum = %d, sMatrixB_colNum = %d", sMatrixA->rowNum,
		sMatrixB->rowNum, sMatrixA->colNum, sMatrixB->colNum);
	sMatrixC->rowNum = sMatrixA->rowNum;
	sMatrixC->colNum = sMatrixA->colNum;
	for (int i = 1; i <= sMatrixB->noneZeroNum; ++i) {
		sMatrixB->data[i].e *= -1;
	}

	Status ret = AddSMatrix(sMatrixA, sMatrixB, sMatrixC);
	CHECK_RET(ret, NONE);

	return RET_OK;
}

/* 算法 5.1，
   求稀疏矩阵 *sMatrix 的转置矩阵 *sMatrixT */
Status TransposeSMatrix(const TSMatrix *sMatrix, TSMatrix *sMatrixT)
{
	CHECK_VALUE(!sMatrix || !sMatrixT, ERR_NULL_PTR, "sMatrix = %p sMatrixT = %p", sMatrix, sMatrixT);
	sMatrixT->rowNum = sMatrix->colNum;
	sMatrixT->colNum = sMatrix->rowNum;
	sMatrixT->noneZeroNum = sMatrix->noneZeroNum;
	if (sMatrixT->noneZeroNum == 0) {
		return RET_OK;
	}

	int noneZeroNumT = 1;
	for (int col = 1; col <= sMatrix->colNum; ++col) {
		for (int i = 1; i <= sMatrix->noneZeroNum; ++i) {
			if (sMatrix->data[i].j != col) {
				continue;
			}

			sMatrixT->data[noneZeroNumT].i = sMatrix->data[i].j;
			sMatrixT->data[noneZeroNumT].j = sMatrix->data[i].i;
			sMatrixT->data[noneZeroNumT].e = sMatrix->data[i].e;
			++noneZeroNumT;
		}
	}

	return RET_OK;
}

/* 算法 5.2，
   快速求稀疏矩阵 *sMatrix 的转置矩阵 *sMatrixT */
Status FastTransposeSMatrix(const TSMatrix *sMatrix, TSMatrix *sMatrixT)
{
	CHECK_VALUE(!sMatrix || !sMatrixT, ERR_NULL_PTR, "sMatrix = %p sMatrixT = %p", sMatrix, sMatrixT);
	sMatrixT->rowNum = sMatrix->colNum;
	sMatrixT->colNum = sMatrix->rowNum;
	sMatrixT->noneZeroNum = sMatrix->noneZeroNum;
	if (sMatrixT->noneZeroNum == 0) {
		return RET_OK;
	}

	int *colNum = (int *)malloc(sizeof(int) * (unsigned long long)(sMatrix->colNum + 1));
	int *firstColNoneZero = (int *)malloc(sizeof(int) * (unsigned long long)(sMatrix->colNum + 1));
	for (int col = 1; col <= sMatrix->colNum; ++col) {
		colNum[col] = 0;
	}

	for (int i = 1; i <= sMatrix->noneZeroNum; ++i) {
		++colNum[sMatrix->data[i].j];
	}

	firstColNoneZero[1] = 1;
	for (int col = 2; col <= sMatrix->colNum; ++col) {
		firstColNoneZero[col] = firstColNoneZero[col - 1] + colNum[col - 1];
	}

	int col, order;
	for (int i = 1; i <= sMatrix->noneZeroNum; ++i) {
		col = sMatrix->data[i].j;
		order = firstColNoneZero[col];
		sMatrixT->data[order].i = sMatrix->data[i].j;
		sMatrixT->data[order].j = sMatrix->data[i].i;
		sMatrixT->data[order].e = sMatrix->data[i].e;
		++firstColNoneZero[col];
	}

	free(colNum);
	free(firstColNoneZero);

	return RET_OK;
}

/* 求稀疏矩阵 *sMatrixA 和 *sMatrixB 的乘积矩阵 *sMatrixC */
Status MultSMatrix(const TSMatrix *sMatrixA, const TSMatrix *sMatrixB, TSMatrix *sMatrixC)
{
	CHECK_VALUE(!sMatrixA || !sMatrixB || !sMatrixC, ERR_NULL_PTR, "sMatrixA = %p, sMatrixB = %p, sMatrixC = %p",
		sMatrixA, sMatrixB, sMatrixC);
	CHECK_VALUE((sMatrixA->colNum != sMatrixB->rowNum), ERR_PARA, "sMatrixA_colNum = %d, sMatrixB_rowNum = %d",
		sMatrixA->colNum, sMatrixB->rowNum);
	TSMatrix tempMatrix = { 0 };
	tempMatrix.rowNum = sMatrixB->colNum;
	tempMatrix.colNum = sMatrixA->rowNum;
	tempMatrix.noneZeroNum = 0;
	ElemType *sMatrixARow = (ElemType *)malloc(sizeof(ElemType) * (unsigned long long)(sMatrixA->rowNum + 1));
	ElemType *sMatrixBCol = (ElemType *)malloc(sizeof(ElemType) * (unsigned long long)(sMatrixB->rowNum + 1));
	CHECK_VALUE(!sMatrixARow || !sMatrixBCol, ERR_MEMORY_ALLOCATE, "sMatrixARow = %p, sMatrixBCol = %p",
		sMatrixARow, sMatrixBCol);
	for (int i = 1; i <= sMatrixB->colNum; ++i) {
		for (int j = 1; j <= sMatrixA->rowNum; ++j) {
			sMatrixARow[j] = 0;
		}

		for (int j = 1; j <= sMatrixB->rowNum; ++j) {
			sMatrixBCol[j] = 0;
		}

		for (int j = 1; j <= sMatrixB->noneZeroNum; ++j) {
			if (sMatrixB->data[j].j == i) {
				sMatrixBCol[sMatrixB->data[j].i] = sMatrixB->data[j].e;
			}
		}

		for (int j = 1; j <= sMatrixA->noneZeroNum; ++j) {
			sMatrixARow[sMatrixA->data[j].i] += sMatrixA->data[j].e * sMatrixBCol[sMatrixA->data[j].j];
		}

		for (int j = 1; j <= sMatrixA->rowNum; ++j) {
			if (sMatrixARow[j] == 0) {
				continue;
			}

			tempMatrix.data[++tempMatrix.noneZeroNum].e = sMatrixARow[j];
			tempMatrix.data[tempMatrix.noneZeroNum].i = i;
			tempMatrix.data[tempMatrix.noneZeroNum].j = j;
		}
	}

	CHECK_VALUE(tempMatrix.noneZeroNum > MAX_SIZE, ERR_PARA, "tempMatrix.noneZeroNum = %d", tempMatrix.noneZeroNum);
	Status ret = TransposeSMatrix(&tempMatrix, sMatrixC);
	CHECK_RET(ret, NONE);
	ret = DestroySMatrix(&tempMatrix);
	CHECK_RET(ret, NONE);
	free(sMatrixARow);
	free(sMatrixBCol);

	return RET_OK;
}

4) main.c

#include "tripleSparseMatrix.h"
#include 

int main(void)
{
	TSMatrix sMatrixA, sMatrixB, sMatrixC, sMatrixCT, sMatrixBT;
	Status ret = CreateSMatrix(&sMatrixA);
	printf("sMatrixA:\n\n");
	ret |= PrintSMatrix(&sMatrixA);
	CHECK_RET(ret, NONE);
	ret = CopySMatrix(&sMatrixA, &sMatrixB);
	printf("\nsMatrixB:\n\n");
	ret |= PrintSMatrix(&sMatrixB);
	CHECK_RET(ret, NONE);
	ret = AddSMatrix(&sMatrixA, &sMatrixB, &sMatrixC);
	printf("\nsMatrixC:\n\n");
	ret |= PrintSMatrix(&sMatrixC);
	CHECK_RET(ret, NONE);
	ret = FastTransposeSMatrix(&sMatrixC, &sMatrixCT);
	printf("\nsMatrixCT:\n\n");
	ret |= PrintSMatrix(&sMatrixCT);
	CHECK_RET(ret, NONE);

	ret = TransposeSMatrix(&sMatrixB, &sMatrixBT);
	ret |= MultSMatrix(&sMatrixA, &sMatrixBT, &sMatrixCT);
	printf("\nsMatrixA * sMatrixBT = :\n\n");
	ret |= PrintSMatrix(&sMatrixCT);
	CHECK_RET(ret, NONE);

	ret |= DestroySMatrix(&sMatrixA);
	ret |= DestroySMatrix(&sMatrixC);
	ret |= DestroySMatrix(&sMatrixCT);
	CHECK_RET(ret, NONE);

	return 0;
}

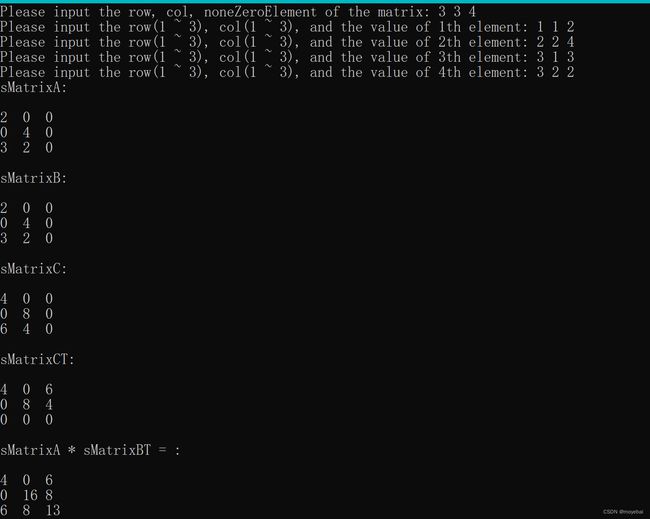
3. 输出结果