数据结构---二叉树链式结构的实现

1. 二叉树链式结构的遍历

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

1.1 前序/中序/后序的递归结构遍历

所谓的前中后序是根据访问根结点操作发生位置先后命名的。
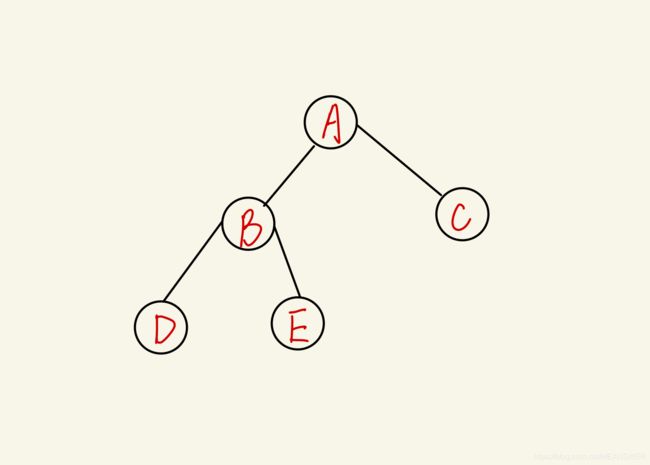
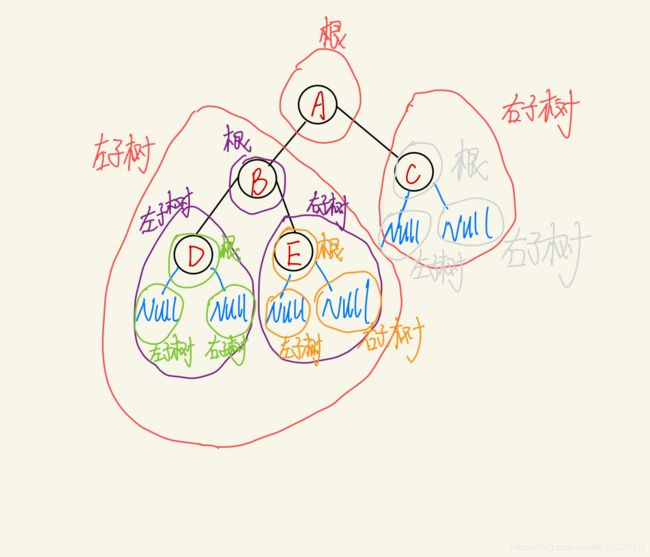
为了能更加好的理解这一部分：首先你要把任意的一个二叉树都看作三个部分①根结点②左子树③右子树，直到根结点为空才算是遍历完全，停止。

1. NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。（简单点的顺序为根 左子树 右子树）

2. LNR：中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。（简单点的顺序为左子树 根 右子树）

3. LRN：后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。（简单点的顺序为左子树 右子树 根）

   图来解释：前序/中序/后序的遍历过程
   

   

前序：

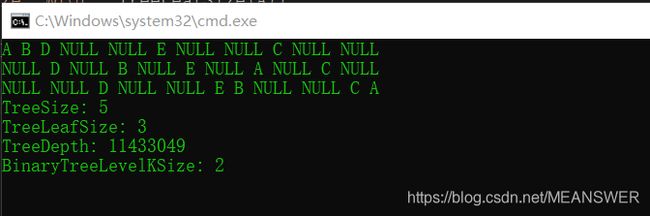
A B D  NULL NULL E NULL NULL C NULL NULL

但是在显示的时候NULL是不显示的所以顺序为：A B D E C

中序：

一定要记住是先从左子树开始遍历，所以要不停的找到左子树为空的时候停止。

NULL D NULL B NULL E NULL A NULL C NULL

在不显示NULL的情况下的顺序为：D B E A C

后序：

NULL NULL D NULL NULL E B NULL NULL C A

在不显示NULL的情况下的顺序为：D B E A C

1.2 层序遍历

除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

2. 完整代码

#include
#include
typedef  char BTDateType;

typedef struct BinaryTreeNode
{
	BTDateType _date;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;

//前序遍历
//（先根遍历）  根 左子树 右子树
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->_date);//先打印根
	PrevOrder(root->_left);
	PrevOrder(root->_right);
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->_left);
	printf("%c ", root->_date);//打印根
	InOrder(root->_right);
}


//后续遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->_left);
	PostOrder(root->_right);
	printf("%c ", root->_date);//打印根
}

//这里的这个size如何解决才是真正需要好好处理思考的问题！
//int size = 0;  但是你遍历全局变量也不好，因为当你两次进行求这个TreeSize值的时候，他的值是累加的，
//int TreeSize(BTNode* root)
//{
//	if (root == NULL)
//		return 0;
//
//	//int size = 0;  这个size是一个局部变量，我每次调用一次我就定义了一次size，所加的size不是同一个值，所以要把这个size变成全局变量
//	size++;
//	TreeSize(root->_left);
//	TreeSize(root->_right);
//	return size;
//}

//如果这里传的是int size 相当于传值，那么我第一次进去是++了，但是第二次进去如果不为空，++的size又不在是原来的了
//所以这里要传址，保证我一直是在通一个size上面进行累加
//void TreeSize(BTNode* root,int* psize)
//{
//	if (root == NULL)
//		return 0;
//	else
//		(*psize)++;
//
//	TreeSize(root->_left, psize);
//	TreeSize(root->_right,psize);
//}

//递归的方式求
int TreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	else
		return 1 + TreeSize(root->_left) + TreeSize(root->_right); //这里很巧妙的避开了这个size值累加的值
}


//求叶子结点的个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	
	if (root->_left == NULL && root->_right == NULL)
		return 1;
	return TreeLeafSize(root->_left) + TreeLeafSize(root->_right);
}

//深度
int TreeDepth(BTNode* root)
{
	//空的话，深度就是0
	if (root == NULL)
		return 0;
	//此时既不是空也不是叶子的时候，我求出左的深度，再求出右的深度，取两个深度中较大的那一个，然后在+1
	int LeftTreeDepth = root->_left;
	int RighttTreeDepth = root->_right;
	//避免掉代码过长导致冗余
	return  LeftTreeDepth > RightTreeDepth ? LeftTreeDepth+1:RightTreeDepth+1;
}

BTNode* CreateNode(char x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	node->_date = x;
	node->_left = NULL;
	node->_right = NULL;
	return node;
}


int main()
{
	BTNode* A = CreateNode('A');
	BTNode* B = CreateNode('B');
	BTNode* C = CreateNode('C');
	BTNode* D = CreateNode('D');
	BTNode* E = CreateNode('E');
	//将他们链起来
	A->_left = B;
	A->_right = C;
	B->_left = D;
	B->_right = E;

	PrevOrder(A);
	printf("\n");

	InOrder(A);
	printf("\n");

	PostOrder(A);
	printf("\n");


	//int sizea = 0;
	//TreeSize(A, &sizea);
	//printf("TreeSize: %d\n", sizea);
	printf("TreeSize: %d\n", TreeSize(A)); 如果使用全局变量size，那么在打印一次size的时候上一次的值就会累加，这里就会变成10

	//int sizeb = 0;
	//TreeSize(B, &sizeb);
	//printf("TreeSize: %d\n", sizeb);


	printf("TreeSize: %d\n", TreeSize(A)); 
	printf("TreeLeafSize: %d\n", TreeLeafSize(A));
	printf("TreeDepth: %d\n", TreeDepth(A));
	getchar();
	return 0;
}

值得注意的就是在计算TreeSize，TreeLeafSize，TreeDepth大小的时候如何去思考？

如果不是用递归，而是你自己定义一个局部的size你会发现在计算的时候他每递归一次都会重新定义一次size，那么你的size也就不是在同一个上面在累加，得到的结果也就不对，但是如果你使用全局变量在定义size的时候，也会有弊端，因为当你在一次去求它的size的时候，这个size会保留上一次size的值，然后累加，也会出现问题。所以你考虑到可以给他传过去一个size变量，但是一定要传址，因为传值的话只是一份临时的拷贝，size还是无法做到累加的效果。

这里的遍历过程是一个递归的思想，如果采用递归的思想把一些特别的想到写出来以后，剩下的不管如何改变，思想都不会变。我要求TreeSize那么除了传的root为空时返回0，其他的情况肯定就是左子树的结点+右子树的结点，当然还要加上root的根结点的1。求TreeLeafSize只有你的左右子树都为空的情况下才能称为叶子结点。求深度TreeDepth那么就是左子树的深度和右子树的深度来比较，取较大的哪一个然后还要加上根结点的深度。

2.1 补充前面代码遗漏的三处

补：①二叉树第K层结点个数
②二叉树查找值为x的结点
③销毁

//二叉树第K层结点个数
//当前树的第K层可以转换成左右子树的第K-1层
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDateType x)
{
	if (root == NULL)
		return NULL;
	if (root->_date == x)
		return root;
	//如果在左边直接找到了，就不用再去右边找了
	BTNode* node = BinaryTreeFind(root->_left, x);
	if (node)
		return node;
	//没有在左边找到，那再去右边找
	node = BinaryTreeFind(root->_right, x);
	if (node)
		return node;
	return NULL;
}

//销毁
void DestoryTree(BTNode* root)
{
	//最好使用后续遍历，如果使用先序遍历你会发现，root被你干掉了，那么你就找不到你的左右子树了
	if (root == NULL)
		return NULL;
	DestoryTree(root->_left);
	DestoryTree(root->_right);
	free(root);
}