数据结构--树形结构之二叉树--C语言

目录

一、树和二叉树

1.树的概念

 2.二叉树的概念

 二、二叉树的存储结构

1.二叉树的顺序存储结构

2.二叉树的链式存储

三、二叉树的遍历

1.前序遍历：

2.中序遍历

3.后序遍历

---

一、树和二叉树

1.树的概念

结点的度：一个结点含有子结点的个数，称为结点的度。如A点的度为6.

叶子节点/终端结点：度为零的结点，也就是没有子结点的结点，如B\C\H\I等结点。

分支结点/非终端节点：度不为零的结点，如D,E,F,G,J。

双亲节点或父节点：若一个节点有子节点，则称这个节点为其子节点的父节点或者双亲节点。

兄弟节点：有相同父节点的节点称为兄弟节点，如图B，C是兄弟节点。

树的度：一棵树中最大的结点的度称为树的度。如图，该树的度为6.

树的高度/层次：树中节点的层次，如图：树的高度为4.

节点的祖先：从根到该节点上的所有节点，如A是所有节点的祖先。

森林：多颗不相交的树叫森林，并查集就是一个森林。

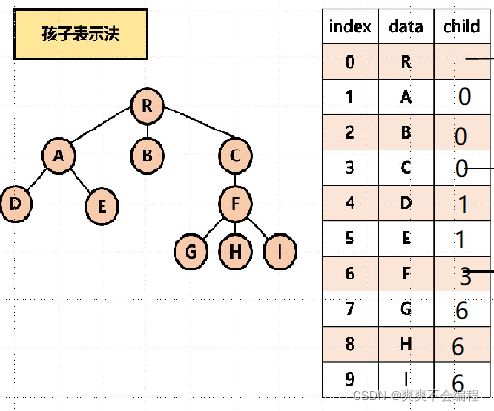
左孩子右兄弟表示方法：

双亲表示法：

树的主要运用于文件目录

 2.二叉树的概念

二叉树是度不超过2的树，有左右之分，不可颠倒，如下图：

完全二叉树和非完全二叉树：

完全二叉树是所有节点按照从左到右依次标号而成的，如图：

 二、二叉树的存储结构

1.二叉树的顺序存储结构

顺序存储结构只适用于完全二叉树，因此，想将顺序存储普通二叉树，必须先将其转化为完全二叉树。

例如下图：

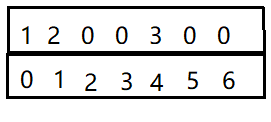
 其顺序存储如下图：

2.二叉树的链式存储

由于顺序存储方式要将普通二叉树转换成完全二叉树，会浪费很多空间，所以链式存储会更适合于二叉树的存储。

 链式节点构成：

Lchild:指向左孩子的指针；

Rchild:指向右孩子的指针；

data:节点的数据域；

节点定义：

typedef struct BinTreeNode
{
	TreeValType data;//数据域
	struct BinTreeNode *lchild, *rchlid;//左右孩子
	struct BinTreeNode *parent;
}BTNode,*BiTree;

创建二叉树：

void CreateBinTree(BinTree *t)
{
	*t = (BinTree*)malloc(sizeof(BinTree));
	(*t)->data = 1;
	(*t)->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->data = 2;
	(*t)->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->rchild->data = 3;
	(*t)->rchild->lchild = NULL;
	(*t)->rchild->rchild = NULL;
	(*t)->lchild->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->lchild->data = 4;
	(*t)->lchild->rchild->data = 5;
	(*t)->lchild->lchild->lchild = NULL;
	(*t)->lchild->lchild->rchild = NULL;
	(*t)->lchild->rchild->rchild = NULL;
	(*t)->lchild->rchild->lchild = NULL;
}

#include
#include
#define TreeValType int

typedef struct BinTreeNode
{
	TreeValType data;//数据域
	struct BinTreeNode *lchild, *rchild;//左右孩子
	struct BinTreeNode *parent;
}BTNode,*BinTree;

void CreateBinTree(BinTree *t)
{
	*t = (BinTree*)malloc(sizeof(BinTree));
	(*t)->data = 1;
	(*t)->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->data = 2;
	(*t)->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->rchild->data = 3;
	(*t)->rchild->lchild = NULL;
	(*t)->rchild->rchild = NULL;
	(*t)->lchild->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->lchild->data = 4;
	(*t)->lchild->rchild->data = 5;
	(*t)->lchild->lchild->lchild = NULL;
	(*t)->lchild->lchild->rchild = NULL;
	(*t)->lchild->rchild->rchild = NULL;
	(*t)->lchild->rchild->lchild = NULL;
}

int main()
{
	BinTree Tree;
	CreateBinTree(&Tree);
	printf("%d\n", Tree->lchild->rchild->data);
	getchar();
	return 0;
}

运行结果：

三、二叉树的遍历

二叉树的基本遍历方法如下：

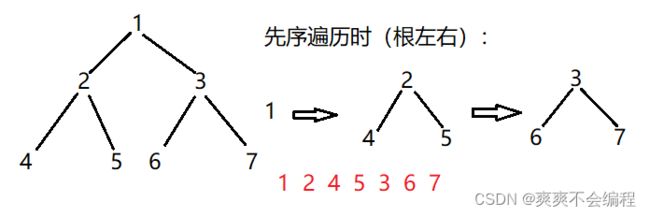
1.前序遍历：

先遍历根，再遍历左子树，在遍历右子树：

 先序遍历采用的是递归的思想：

#include
#include
#define TreeValType int

typedef struct BinTreeNode
{
	TreeValType data;//数据域
	struct BinTreeNode *lchild, *rchild;//左右孩子
	struct BinTreeNode *parent;
}BTNode,*BinTree;

void CreateBinTree(BinTree *t)//创建二叉树
{
	*t = (BinTree*)malloc(sizeof(BinTree));
	(*t)->data = 1;
	(*t)->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->data = 2;
	(*t)->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->rchild->data = 3;
	(*t)->rchild->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->rchild->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->lchild->data = 4;
	(*t)->lchild->rchild->data = 5;
	(*t)->rchild->rchild->data = 7;
	(*t)->rchild->lchild->data = 6;
	(*t)->lchild->lchild->lchild = NULL;
	(*t)->lchild->lchild->rchild = NULL;
	(*t)->lchild->rchild->rchild = NULL;
	(*t)->lchild->rchild->lchild = NULL;
	(*t)->rchild->lchild->lchild = NULL;
	(*t)->rchild->lchild->rchild = NULL;
	(*t)->rchild->rchild->rchild = NULL;
	(*t)->rchild->rchild->lchild = NULL;
}

void displayVal(BTNode * Val)
{
	
	printf("%d", Val->data);
}

//先序遍历二叉树
void PreOrderTraverse(BinTree t)
{
	if (t != NULL)
	{
		displayVal(t);
		PreOrderTraverse(t->lchild);//访问左孩子
		PreOrderTraverse(t->rchild);//访问右孩子
	}
	return;
}

int main()
{
	BinTree Tree;
	CreateBinTree(&Tree);
	printf("先序遍历：\n");
	PreOrderTraverse(Tree);
	getchar();
	return 0;
}

运行结果：

递归的底层是栈的存取结构思想，故二叉树的先序遍历既可以直接采用递归思想实现，也可以使用栈的存储结构模拟递归的思想实现

非递归实现：

非递归的基本思路：使用堆栈

遇到一个结点，就访问它，并去遍历它的右子树；

如果有右孩子，压栈;

然后先序再去遍历它的左孩子。

#include
#include
#include

#define TreeValType int
int top = -1;//初始栈顶元素所在位置

//构造节点结构体
typedef struct BinTreeNode
{
	TreeValType data;
	struct BinTreeNode * lchild, *rchild;
}BTNode,*BTree;

//初始化树的函数
void CreateBinTree(BTree *t)
{
	*t = (BTree*)malloc(sizeof(BTree));
	(*t)->data = 1;
	(*t)->lchild = (BTree*)malloc(sizeof(BTree));
	(*t)->rchild = (BTree*)malloc(sizeof(BTree));
	(*t)->lchild->data = 2;
	(*t)->rchild->data = 3;
	(*t)->lchild->lchild = (BTree*)malloc(sizeof(BTree));
	(*t)->lchild->rchild = (BTree*)malloc(sizeof(BTree));
	(*t)->lchild->lchild->data = 4;
	(*t)->lchild->rchild->data = 5;
	(*t)->rchild->lchild = (BTree*)malloc(sizeof(BTree));
	(*t)->rchild->rchild = (BTree*)malloc(sizeof(BTree));
	(*t)->rchild->lchild->data = 6;
	(*t)->rchild->rchild->data = 7;
	(*t)->lchild->lchild->lchild = NULL;
	(*t)->lchild->lchild->rchild = NULL;
	(*t)->lchild->rchild->lchild = NULL;
	(*t)->lchild->rchild->rchild = NULL;
	(*t)->rchild->lchild->lchild = NULL;
	(*t)->rchild->lchild->rchild = NULL;
	(*t)->rchild->rchild->lchild = NULL;
	(*t)->rchild->rchild->rchild = NULL;
}
//前序遍历使用的进栈函数
void push(BTree** a, BTNode* Val)
{
	a[++top] = Val;
}

//出栈函数
void pop()
{
	if (top ==-1)
	{
		return;
	}
	top--;
}

void displayVal(BTNode* Val)
{
	printf("%d",Val->data);
}

//获取栈顶元素
BTNode* gettop(BTNode**a)
{
	return a[top];
}
//先序遍历非递归算法
	void preOrderTraverse(BTree tree)
	{
		BTNode* a[20];//定义顺序栈
		BTNode* p;//定义临时指针
		push(a, tree);
		while (top != -1)
		{
			p = gettop(a);//取栈顶元素
			pop();//弹栈
			while (p)
			{
				displayVal(p);
				//如果结点有右孩子，右孩子进栈
				if (p->rchild)
				{
					push(a, p->rchild);
				}
				p = p->lchild;//一直指向根节点的最后一个左孩子
			}
		}
	}
	int main()
	{
		BTree tree;
		CreateBinTree(&tree);
		printf("先序遍历：\n");
		preOrderTraverse(tree);
		getchar();
		return 0;
	}

运行结果：

与前面运行结果一致。

2.中序遍历

中序遍历：左子树，根节点，右子树

 递归实现：

#include
#include
#define TreeValType int

typedef struct BinTreeNode
{
	TreeValType data;
	struct BinTreeNode * lchild, *rchild;
}BTNode,*BinTree;

void CreateBinTree(BinTree *t)
{
	*t = (BinTree*)malloc(sizeof(BinTree));
	(*t)->data = 1;
	(*t)->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->data = 2;
	(*t)->rchild->data = 3;
	(*t)->rchild->lchild= (BinTree*)malloc(sizeof(BinTree));
	(*t)->rchild->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->lchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->rchild = (BinTree*)malloc(sizeof(BinTree));
	(*t)->lchild->lchild->data = 4;
	(*t)->lchild->rchild->data = 5;
	(*t)->rchild->lchild ->data = 6;
	(*t)->rchild->rchild->data = 7;
	(*t)->lchild->lchild->lchild = NULL;
	(*t)->lchild->lchild->rchild = NULL;
	(*t)->lchild->rchild->lchild = NULL;
	(*t)->lchild->rchild->rchild = NULL;
	(*t)->rchild->lchild->lchild = NULL;
	(*t)->rchild->lchild->rchild = NULL;
	(*t)->rchild->rchild->lchild = NULL;
	(*t)->rchild->rchild->rchild = NULL;
}

//输出节点本身的值
void displayVal(BTNode * Val)
{
	printf("%d", Val->data);
}

//中序遍历
void MidOrderTraverse(BinTree t)
{
	if (t != 0)
	{
		MidOrderTraverse(t->lchild);//遍历左孩子
		displayVal(t);
		MidOrderTraverse(t->rchild);
	}
	//节点为空，返回上一层
	return;
}

int main()
{
	BinTree tree;
	CreateBinTree(&tree);
	printf("中序遍历：\n");
	MidOrderTraverse(tree);
	getchar();
}

运行结果：

3.后序遍历

后序遍历：左右根；

#include 
#include 
#include
#define TreevaleType int
//构造结点的结构体
typedef struct BiTNode{
	TreevaleType data;//数据域
	struct BiTNode *lchild, *rchild;//左右孩子指针
}BiTNode, *BiTree;
//初始化树的函数
void CreateBiTree(BiTree *T){
	*T = (BiTNode*)malloc(sizeof(BiTNode));
	(*T)->data = 1;
	(*T)->lchild = (BiTNode*)malloc(sizeof(BiTNode));
	(*T)->rchild = (BiTNode*)malloc(sizeof(BiTNode));

	(*T)->lchild->data = 2;
	(*T)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
	(*T)->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
	(*T)->lchild->rchild->data = 5;
	(*T)->lchild->rchild->lchild = NULL;
	(*T)->lchild->rchild->rchild = NULL;
	(*T)->rchild->data = 3;
	(*T)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
	(*T)->rchild->lchild->data = 6;
	(*T)->rchild->lchild->lchild = NULL;
	(*T)->rchild->lchild->rchild = NULL;
	(*T)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
	(*T)->rchild->rchild->data = 7;
	(*T)->rchild->rchild->lchild = NULL;
	(*T)->rchild->rchild->rchild = NULL;
	(*T)->lchild->lchild->data = 4;
	(*T)->lchild->lchild->lchild = NULL;
	(*T)->lchild->lchild->rchild = NULL;
}

//模拟操作结点元素的函数，输出结点本身的数值
void displayVale(BiTNode* vale){
	printf("%d ", vale->data);
}
//后序遍历
void LastOrderTraverse(BiTree T){
	if (T) {
		LastOrderTraverse(T->lchild);//遍历左孩子
		LastOrderTraverse(T->rchild);//遍历右孩子
		displayVale(T);//调用操作结点数据的函数方法
	}
	//如果结点为空，返回上一层
	return;
}
int main() {
	BiTree Tree;
	CreateBiTree(&Tree);
	printf("后序遍历: \n");
	LastOrderTraverse(Tree);
	getchar();
}

运行结果：

与手工迭代一致。 

参考：二叉树后序遍历（递归与非递归）算法及C语言实现 (biancheng.net)