【数据结构】线段树

算法提高课笔记 还未更新完

原理

时间复杂度：O(logn)

线段树是一棵二叉树，把一段区间分成多个部分

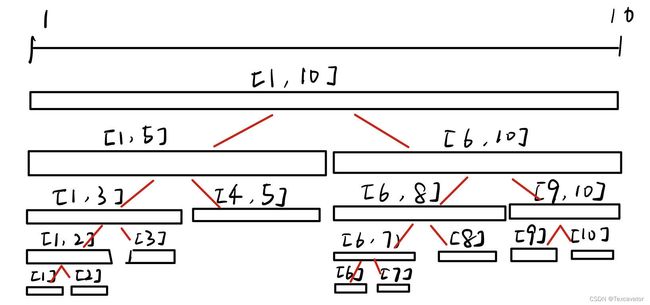
类似堆的方式，用一维数组存整棵树

对于编号x的结点：

• 父结点 $\lfloor x\rfloor$，表示为 x >> 1
• 左子树 $2x$，表示为 x << 1
• 右子树 $2x+1$，表示为 x << 1 | 1

对于长度为n的区间，最坏估计有 $4n-1$ 个结点，因此 开数组时空间一般开 $4n$

pushup

由子结点计算父结点的信息

模板：

// u表示当前树中结点编号 lr表示树中结点左右子结点
void pushup(Node &u, Node &l, Node &r)
{
    /* 此处用[l]和[r]的值更新[u] */
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

build

将一段区间初始化为线段树

1. 首先记录下当前区间的左右端点，如果左端点和右端点相等就直接返回
2. 如果不相等，取中间值 mid，然后分别递归左右两段

模板：

// u表示当前树中结点编号 lr表示区间左右端点
void build(int u, int l, int r)
{
    if (l == r) // 左右端点相同表示到达叶子结点
    {
        tr[u] = {    }; // 创建该结点
    }
    else
    {
        tr[u].l = l, tr[u].r = r;
        int mid = l + r >> 1; // 取中间值
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); // 分别构造左右两棵子树
        pushup(u); // 利用pushup更新该点
    }
}

modify

修改单点或区间（需要用到push_down操作）

修改单点模板：

// u为当前树中结点编号 要把x位置的值更新为v
void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x) // 到达叶子结点 直接更新
    {
        tr[u] = {     };
    }
    else
    {
        int mid = tr[u].l + tr[u].r >> 1; // 取中间值
        if (x <= mid) modify(u << 1, x, v); // 要更新的位置在左半部分
        else modify(u << 1 | 1, x, v); // 要更新的位置在右半部分
        pushup(u); // 更新此位置结点
    }
}

修改区间模板：

void modify(int u, int l, int r, int d)
{
    if (tr[u].l >= l && tr[u].r <= r) // 当前树中结点在所求区间之内
    {
        tr[u].sum += (i64)(tr[u].r - tr[u].l + 1) * d; // 更新区间信息
        tr[u].add += d; // 打上懒标记
    }
    else // 当前树中结点不在所求区间之内
    {
        pushdown(u); // 将懒标记向下传递
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, d); // 与左半段有重合部分就更新左半段
        if (r > mid) modify(u << 1 | 1, l, r, d); // 与左半段有重合部分就更新左半段
        pushup(u); // 由于modify修改了区间结点的信息，所以被修改的结点的祖先结点都需要重算一遍
    }
}

query

查询区间信息

假设我们要查询某区间的最大值

定义 [l, r] 为我们要查询的区间，[Tl, Tr] 为树中结点（当前我们正在维护的区间），这两个区间会有如下两种关系：

• $[Tl,Tr]\subset [l,r]$，树中结点完全包含在要查询的区间内部
  这种情况直接返回当前区间最大值即可
• $[l,r]\bigcap [Tl,Tr]\ne \varnothing$，二者有交集
  和左边有交集就递归到左边做一遍，和右边有交集就递归到右边做一遍
  即l > mid只递归右边，r <= mid只递归左边，否则左右都递归

模板：

Node query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u]; // 当前区间在被查询区间之内 直接返回
    else
    {
        int mid = tr[u].l + tr[u].r >> 1; // 取中间值
        if (r <= mid) return query(u << 1, l, r); // 被查询区间在当前区间左半部分
        else if (l > mid) return query(u << 1 | 1, l, r); // 被查询区间在当前区间右半部分
        else // 被查询区间横跨当前区间的左右两部分
        {
            auto left = query(u << 1, l, r); // 计算出左半部分值
            auto right = query(u << 1 | 1, l, r); // 计算出右半部分值
            Node res;
            pushup(res, left, right); // 更新结果
            return res;
        }
    }
}

pushdown（懒标记 / 延迟标记）

将父结点的修改更新到子结点

单点修改可以只用pushup，涉及到区间修改就需要使用pushdown

懒标记 ：在当前树中结点上打上懒标记，就表示对以当前树中结点为根结点的每一个子树都进行操作（根结点自己不用操作）

那么懒标记怎么进行传递呢？

焗个栗子：比如我们在蓝色的这一段区间上打上懒标记

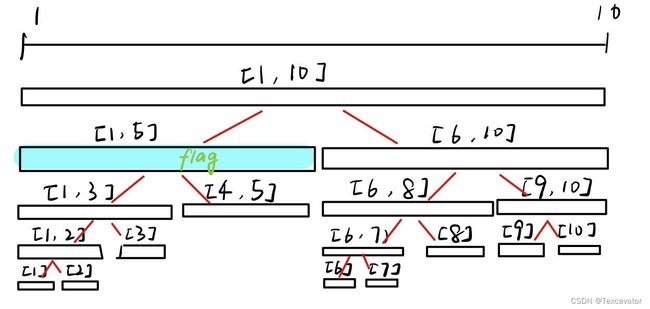
每当我们需要遍历蓝色区间结点下方的子结点时，我们就把懒标记传递给下一层结点，同时把根结点的懒标记删除，就像这样：

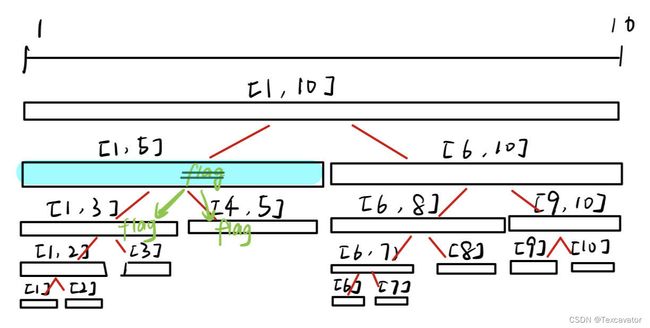
当然，除了传递标记，我们还需要对线段树中记录的值进行更新，比如说这个线段树记录的是区间和，打上懒标记表示这一段区间每一个数都要加上a，那么我们在传递懒标记的同时，还需要让下方结点的区间和加上(r - l + 1) * a，其中(l - r + 1)表示下方被更新结点的区间长度

以此类推，每当我们需要遍历下方结点时，就把懒标记向下传，并更新下方结点的值

以上就是pushdown操作的基本内容

模板：

void pushdown(int u)
{
    auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
    if (root.add) // 当前结点有懒标记 向下传递
    {
        left.add += root.add, left.sum += (i64)(left.r - left.l + 1) * root.add;
        right.add += root.add, right.sum += (i64)(right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}

扫描线法