基于PyTorch框架下神经网络的基础知识及使用

1 神经网络的搭建

如图一所示，在PyTorch的官网中我们可以看到Docs下面对PyTorch分了不同的块，比如：PyTorch是关于PyTorch的一些官方文档、torchaudio是处理语音的、torchtext是处理文本的、torchvision是处理图像的等。
图一：

我们点开PyTorch的官方文档会发现左边有一些PyTorch API，这就是我们经常提到的package,就是不同的包（也就相当于PyTorch提供的一些工具）。关于神经网络的一些工具就主要在torch.nn这个API里面。
在torch.nn里面又分为了不同的类别，第一个是Containers（容器、骨架）,它主要是对我们的神经网络定义了一些骨架（就是定义了一些结构），只要往这些结构里添加一些不同的内容，然后就构成了我们的一个神经网络。后面的类别都是需要往前面定义的骨架里面填充的东西，比如说：卷积层、池化层等。
点开Containers，我们常用的是module模块（它是对所有神经网络模型一个基本的类，就是给我们所有神经网络提供一个基本的模型）。
点开module，可以看到我们搭建的神经网络都是从torch.nn.Module这个类当中进行一个继承。
我们可以看一下官网当中的这个小案例：

import torch.nn as nn
import torch.nn.functional as F

#这里定义了一个神经网络叫做Model，它继承了nn.module这个类，就相当于nn.module是一个父类，给我们所有神经网络提供了一个模板，我们继承它就是把这个模板拿来用（如果里面有不满意的东西，对其进行一个修改即可）。
#这个类里面主要包括两个方法，分别为：__init__方法和forward方法。
#__init__方法：就是我们进行一个初始化，初始化过程中首先 super(Feihan,self).__init__()这个是必须有的，后面部分则是需要自己写的。
#forward方法：这个方法是非常重要的，就是前向传播的函数。
#比如：图二中的蓝色块相当于一个神经网络，我们有一个输入input需要送到我们的神经网络当中，然后这个神经网络就会给我们一个output输出。这个神经网络经过的一个运算步骤其实就是forward方法，这其实是一个前向传播。还有一种方法是反向传播。
class Model(nn.module)：
      def __init__(self)：
          #下面这个语句是这个方法里面的固定语句
          super(Feihan,self).__init__()
          #下面我们就可以自己写所需要的语句了，比如：
          self.conv1 = nn.Conv2d(1,20,5)
          self.conv2 = nn.Conv2d(20,20,5)
      #self指这个类，是必备的
      #它定义了一个x,其实这里可以是任意的，只是把它命名为了x而已，就相当于输入是x   
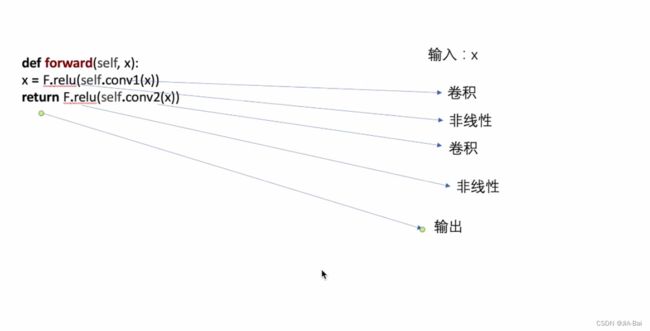
      def forward(self,x):
          #下面这两句的运算过程如图三所示，即图三就是这两句的处理流程
          x = F.relu(self.conv1(x))
          return F.relu(self.conv2(x))

图二：
图三：

下面我们进行一个自己的神经网络基本骨架的搭建：
nn_module.py:

from torch import nn
import torch

#我们首先搭建一个神经网络，给这个神经网络取名为Feihan
#然后我们需要继承Torch.nn给我们提供的一个module,叫做nn.module
#这样的话我们也就需要在前面进行一个导入：from torch import nn
class Feihan(nn.module)：
      #需要重写module里面的那两个方法，分别为：__init__方法和forward方法。
      #重写方法这里有个快捷操作，就是选择Pycharm上面那一栏当中的Code,它会出现一个Generate选项，点击之后我们选择Override Methods这个选项，然后再选择__init__(self：Module)即可自动完成__init__方法的重写。
      def __init__(self)：
          #下面这个语句是这个方法里面的固定语句
          super(Feihan,self).__init__()
          #下面我们就可以自己写所需要的语句了，比如：
          #self.conv1 = nn.Conv2d(1,20,5)
          #self.conv2 = nn.Conv2d(20,20,5)

      #比如在forward方法当中我们要给它一个input
      def forward(self,input):
          output = input + 1
          return output
      #这里我们写的这个神经网络其实很简单：就是你给神经网络一个输入，它只是简单的把这个输入加1，然后就进行一个返回作为神经网络的输出。
      #这样我们就定义好了我们神经网络的一个模板

#首先用上面这个模板来创建一下我们的神经网络
feihan = Feihan()
#给一个输入为x
x = torch.tensor(1.0)
#上面这里用到了torch.tensor，所以我们在前面需要导入一下：import torch
#接下来把x输入到我们的神经网络当中,且进行一个输出
output = feihan(x)
#对output进行一个打印输出
print(output)

2 神经网络中神经结构的使用

Convolution Layers:卷积层
nn.Conv1d：一维
nn.Conv2d：二维
nn.Conv3d：三维
比如说：
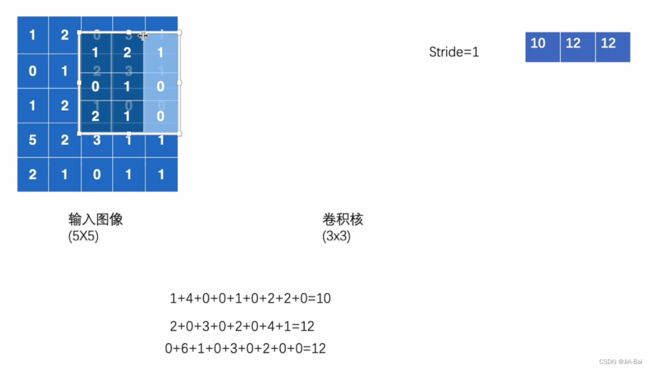
图四当中左边是一个55（5行5列）的输入图像，其中每一格的数字代表它在这一格像素当中的颜色显示；中间有一个33（3行3列）的卷积核；右边是放输出结果的地方。
图四：
做卷积的过程：

1. 如图五，其实就是先将卷积核从左上角放进输入图像中，然后对应位进行相乘，然后将乘积加在一起。这里得到的结果是10，我们将结果进行一个输出（也就是图中的右边）。

图五：

2. 如果此时stride=1，也就是步长等于1，我们将此时在左上角的卷积核向右平移2步，得到图六的结果。同样，如果此时stride=2，也就是步长等于2，我们将此时在左上角的卷积核向右平移2步。

图六：

3. 发现此时我们还可以向右移动进行匹配，我们重复上面的步骤2，则会得到图七的结果。

图七：

4. 接下来发现向右移动已经不能继续进行匹配了，此时我们就需要从左上角开始向下进行平移一步的操作（stride=1），则会得到图八的结果。stride=1操作类似，即需要从左上角开始向下进行平移2步的操作。

图八：

5. 接着我们在步骤4的位置上继续进行步骤3的操作直至这一行全部走完。
6. 对于列操作也和前面的行操作一样，直到这个输入图像完全被这个卷积核卷积完，则会得到图九的结果，即卷积后的输出。

图九(这里一不下心计算错了，应该把卷积结果中的第三行第一列的结果修改为13)：

我们将上面的卷积过程用代码表示，则如下所示：
nn_conv.py

import torch
import torch.nn.functional as F
#此时的输入数据(就是上面的输入图像)是一个二维矩阵[[]]
input = torch.tensor([[1,2,0,3,1],
                      [0,1,2,3,1],
                      [1,2,1,0,0],
                      [5,2,3,1,1],
                      [2,1,0,1,1]])
#此时的卷积核我们把它命名为kernel,也是一个二维矩阵[[]]   
kernel = torch.tensor([[1,2,1],
                       [0,1,0],
                       [2,1,0]])    
                       
#接下来就可以用Conv2d这个卷积函数，验证一下我们上图所做的卷积结果是否是正确的。
#但是在使用这个函数的时候，我们发现需要知道input、kernel的尺寸，所以接下来进行此操作。    
#打印查看input、kernel的尺寸
print(input.shape)
print(kernel.shape)
#此时运行结果为torch.Size([5,5])和torch.Size([3,3])，只能看出高和宽，但这是不满足Conv2d这个卷积函数的要求的。
#所以接下来我们就需要学习一个Pytorch给我们提供的一个尺寸变换功能，就是torch.reshape()。
#按住Ctrl+p你会发现它要求得输入就是你要变换的数据，就将我们上面的input放进去；接着还有一个参数是输入想变换的尺寸的大小。
#因为像input这个二维矩阵的话，5*5可以想象一下就是一个平面，一个平面的话它的通道就是1，batchsize肯定也为1
#所以下面这句话第一个1是batchsize=1，第二个1是通道为1，第三四个5是5*5的意思。
#把torch.reshape(input,(1,1,5,5))整体赋值给了一个新的input。     
input = torch.reshape(input,(1,1,5,5))  
#kernel同理可得：
kernel = torch.reshape(kernel,(1,1,3,3))  
#然后我们打印查看input、kernel的尺寸
print(input.shape)
print(kernel.shape)   

#接下来就可以正常使用conv2d这个卷积函数，验证一下我们上图所做的卷积结果是否是正确的。      
#一般使用这个函数需要在前面导入一下：import torch.nn.functional as F
#input:输入(我们需要给它提供一个输入)
#weight:权重（卷积核）
#bias:偏置
#stride:步径，默认值是1
#padding:对输入图像的上下左右进行一个填充，默认情况下为0，是不进行填充的。如果此时设置为padding=1，那我们对图四的输入图像进行填充以后的图像就如下面的图十所示了。
output = F.conv2d(input,kernel,stride=1)
#打印查看一下卷积结果，因为卷积结果赋值给了output,所以我们在这里打印一下output
print(output)
#或者把stride设置为2进行一个输出结果的查看
output2 = F.conv2d(input,kernel,stride=2)
print(output2)
#或者把stride和padding都设置为1进行一个输出结果的查看
output3 = F.conv2d(input,kernel,stride=1,padding=1)
print(output3)

图十：

3 神经网络当中的一些基本结构

3.1 卷积层

神经网络-卷积层(Convolution Layers)的使用：
一个实例
nn_conv2d.py

#卷积层中Conv2d的使用
#这个实例数据集的选取，我们就拿torchvision下的CIFAR（CIFAR10）这个数据集来进行一个输入
import torch
import torchvision
from torch.utils.data import DataLoader
from torch import nn
from torch.utils.ensorboard import SummaryWriter

#获取数据集
dataset = torchvision.datasets.CIFAR10(root="./dataset",train=False,transform=torchvision.transforms.ToTensor(),download=True)
#加载数据到神经网络中去
dataloader = Dataloader(dataset,batch_size=64)

#搭建神经网络
class Feihan(nn.module)：
      def __init__(self)：
          super(Feihan,self).__init__()
          #定义一个卷积层
          #这里使用到Conv2d，下面是Conv2d中的一些参数定义：
             #in_channels：输入图像的通道数，像彩色图像一般就是3个通道。比如上面图四中输入图像的通道数就是1。
             #out_channels：通过卷积以后的输出结果的通道数。如果我们此时把out_channels设置为    1，得到的结果则和图九没有什么区别。但是如果我们把out_channels设置为2，则会产生两个卷积核，我们用这两个卷积核分别进行卷积，得到的结果则如图十一所示，然后我们得到的最终结果需要把图十一得到的那两个输出结果的对应位置进行相加，如图十二所示。我们做算法的时候就会发现他们会不断地增加这个channel数。
             #kernel_size:卷积核的大小，比如：我们写一个3，就代表我们定义了一个3*3的卷积核；也可以定义不规则的卷积核，比如写一个（1，2），就代表我们定义了一个1*2的卷积核。
             #！！！要注意kernel_size只是定义了一个卷积核的大小，就是在我们搭建这个卷积层的时候我们只需要定义一个kernel_size的大小，其中的具体数字不需要进行设置。这些卷积核的参数，也就是其中的具体数字是从我们的分布当中进行一个采样得到的，你就可以想象它满足一定的分布，这个数其实取多少都无所谓，因为我们在实际训练神经网络的过程中，其实就是对这个kernel（卷积核）当中的一些参数进行不断的调整，所以其中的具体数字是会在训练过程中不断进行一个调整。
             #stride:卷积核在输入图像当中进行卷积过程中横向和纵向的步径大小。
             #padding:对输入图像的上下左右进行填充，默认情况下为0，是不进行填充的。
             #padding_mode:定义上面的这个padding是以什么样的方式进行填充的,我们一般情况下都是选择"zeros",就是在把padding填充的地方都设置为0。
             #dilation:定义的是进行卷积过程中卷积核之间的距离，就是卷积核当中每一格元素（就是每一个小格）之间的距离（比如说每一小格之间插一个1，就是每一小格之间空一个小格），这里我们一般把它叫做空洞卷积，但一般不常用。
             #groups:这个我们一般常年设置为1。
             #bias:我们一般常年设置为True,就是给它加一个偏置。
          #因为是彩色图像所以输入通道为3层
          #我们在这里把输出通道设置为6层
          #卷积核的大小就设置为3
          self.conv1 = Conv2d(in_channels=3,out_channels=6,kernel_size3,stride=1,padding=0)
          #现在网络当中就有了一个卷积层

      def forward(self,x):
          #对x进行一个卷积
          x = self.conv1(x)
          return x

#初始化这个网络
feihan = Feihan()
#这个网络结构很简单，我们直接print即可
print(feihan)

##我们还可以把这个数据集里的每一张图片放在这个神经网络当中看一下
##for data in dataloader:
     ##imgs,targets = data
     ##output = feihan(imgs)
     ###卷积前imgs的尺寸
     ##print(imgs.shape)
     ###运行后结果：torch.Size([64,3,32,32])
     ###代表的意思是batch_size=64（每次取64个）,imgs为3通道彩色图片，大小为32*32
     
     ###卷积后imgs的尺寸
     ##print(output.shape)
     ###运行后结果：torch.Size([64,6,30,30])
     ###代表的意思是batch_size=64（每次取64个）,卷积后imgs为6通道,经过卷积图片尺寸变小了，大小为30*30
     
###如果想要更直观的显示则需要使用Tensorboard
###writer = SummaryWrite("logs")
###step = 0
###for data in dataloader:
     ###imgs,targets = data
     ###output = feihan(imgs)
     ###print(imgs.shape)
     ###print(output.shape)
     ####输入时候的大小：torch.Size([64,3,32,32])
     ###writer.add_images("input",imgs,step)
     
     ####输出时候的大小：torch.Size([64,6,30,30])
     ####因为此时通道数为6，图片会无法显示，所以会进行报错
     ####这里我们采取一个不太严谨的解决方法，那就是将"output"reshape一下，进行一下尺寸的变换
     ####我们不知道第一个数字写多少时，就写成-1，它会根据后面三个数字进行一个计算的
     ###output = torch.reshape(output,(-1,3,30,30))
     ###writer.add_images("output",output,step)
     ####按理来说这个图片在一页上面应该也是64张的（这64张就是3通道的），但是我们这里是6通道，只是变换成了3通道的显示形式，所以这个图片在一页上面应该是64*2张的。
     ###step = step + 1
writer.close()

图十一：

图十二：

3.2 池化层

神经网络-池化层（Pooling layers）的使用：
nn.MaxPool2d: 最大池化，也叫下采样
nn.MaxUnpool2d: 上采样
比如说：
图十三当中左边是一个55（5行5列）的输入图像，其中每一格的数字代表它在这一格像素当中的颜色显示；中间有一个3*3（3行3列）的池化核；右边是放输出结果的地方。
图十三：
做最大池化的过程（注意我们这里选用的是最大池化）：

1. 如图十四，其实就是先将池化核从左上角放进输入图像中，然后取被覆盖部分中最大的数字作为结果（因为这里选用的是最大池化）。这里得到的结果是2，我们将结果进行一个输出（也就是图中的右边）。

图十四：

2. 此时kernel_size=3，则stride默认也等于3，也就是步长等于3，我们将此时在左上角的池化核向右平移3步，发现原图不够了，是否需要接受填充的部分？如果此时ceil_mode设置为True，则要接受填充的部分，进行一个结果输出；如果此时ceil_mode设置为False，则不用接受填充的部分，则没有一个结果的输出。也就是得到图十五的结果。

图十五：

3. 接下来发现向右移动已经不能继续进行匹配了，此时我们就需要从左上角开始向下进行平移三步的操作（stride=3），则会得到图十六的结果。

图十六：

4. 对于列操作也和前面的行操作一样，直到这个输入图像完全被这个池化核池化完，则会得到图十七的结果，即池化后的输出。

图十七：
我们将上面的池化过程用代码表示，则如下所示：
nn_maxpool.py

#卷积层中MaxPool2d的使用
import torch
from torch import nn
from torch.nn import MaxPool2d

#此时的输入数据(就是上面的输入图像)是一个二维矩阵[[]]
#下面如果不写dtype=torch.float32这句话就会报错，因为最大池化不能使用Long这个数据类型，所以我们一般用浮点数
input = torch.tensor([[1,2,0,3,1],
                      [0,1,2,3,1],
                      [1,2,1,0,0],
                      [5,2,3,1,1],
                      [2,1,0,1,1]],dtype=torch.float32)
                      
#接下来就可以用maxpool2d这个池化函数，验证一下我们上图所做的池化结果是否是正确的。
#但是在使用这个函数的时候，我们发现要求的input需要知道batchsize、channel、高、宽，所以接下来进行此操作。 
#第一个-1代表想让它自己计算这个batchsize；
#第二个1因为我们只有一层，所以它的channel值1；
#第三四个5是5*5的意思。
input = torch.reshape(input,(-1,1,5,5))  
print(input.shape)

#接下来就可以写我们的神经网络了
class Feihan(nn.module)：
      def __init__(self)：
          super(Feihan,self).__init__()
          #定义一个最大池化层
          #这里使用到MaxPool2d，下面是MaxPool2d中的一些参数定义：
             #kernel_size:设置的用来取最大值的窗口，跟之前学的卷积层一样，比如：我们设置为3的话，就会生成一个3*3的窗口（池化核）；也可以定义不规则的池化核，比如写一个（1，2）就代表我们定义了一个1*2的池化核。
             #stride:步径大小，默认值是kernel_size的大小
             #padding:对输入图像的上下左右进行填充，默认情况下为0，是不进行填充的。
             #dilation:和卷积层类似，我们一般情况下不对它进行设置
             #ceil_mode:设置为True的时候，就会使用ceil（向上取整）这种模式，而不是floor（向下取整）这种模式。默认情况下取的是False。
             #一般使用这个函数需要在前面导入一下：from torch.nn import MaxPool2d
          self.maxpool1 = MaxPool2d(kernel_size=3,ceil_mode=True)
          #或者还可以试试这样池化： self.maxpool1 = MaxPool2d(kernel_size=3,ceil_mode=False)

       def forward(self,input):
          #对input进行一个池化
          output = self.conv1(input)
          return output

#初始化这个网络
feihan = Feihan()
output = feihan(input)
print(output)

最大池化的作用： 我们既可以保留输入数据的特征，同时又可以减小数据量。数据量的减少对于整个网络来说计算参数也就减少了，就会训练的更快。比如说：我们看视频时有1080p的,有720p的，720p就是经过1080p经过池化后产生的，既保留了输入数据的特征，又减小了视频的尺寸大小。
一个实例
nn_maxpool2d.py

#卷积层中MaxPool2d的使用
#这个实例数据集的选取，我们就拿torchvision下的CIFAR（CIFAR10）这个数据集来进行一个输入
import torch
from torch import nn
from torch.nn import MaxPool2d
import torchvision
from torch.utils.data import DataLoader
from torch.utils.ensorboard import SummaryWriter

#获取数据集
dataset = torchvision.datasets.CIFAR10(root="./dataset",train=False,transform=torchvision.transforms.ToTensor(),download=True)
#加载数据到神经网络中去
dataloader = Dataloader(dataset,batch_size=64)

#接下来就可以写我们的神经网络了
class Feihan(nn.module)：
      def __init__(self)：
          super(Feihan,self).__init__()
          self.maxpool1 = MaxPool2d(kernel_size=3,ceil_mode=True)
          #或者还可以试试这样池化： self.maxpool1 = MaxPool2d(kernel_size=3,ceil_mode=False)

       def forward(self,input):
          #对input进行一个池化
          output = self.conv1(input)
          return output

#初始化这个网络
feihan = Feihan()

#如果想要比较直观的显示则需要使用Tensorboard
writer = SummaryWrite("logs")
step = 0

for data in dataloader:
     imgs,targets = data
     writer.add_images("input",imgs,step)
     output = feihan(imgs)
     writer.add_images("output",output,step)
     step = step + 1
writer.close()

3.3 非线性激活

神经网络-非线性激活(Non-Linear Activations)的使用：
非线性激活主要是为了给我们的神经网络中引入一些非线性的特征，因为网络当中非线性越多的话，你才能训练出符合各种曲线、各种特征的一个模型，要不然模型的泛化能力就不够好。比如其中最常见的ReLU。
ReLU这个激活方法的具体图像如图十八所示，我们可以看到当input（输入）>=0的时候，output（输出）就取input的原始值，input（输入）<=0,output（输出）就会被截断，全部取为0。
图十八：
一个实例进行具体理解：
nn_relu.py

#对ReLU非线性激活方法进行一个具体的理解
import torch
from torch import nn
from torch.nn import ReLU

#用一个二维矩阵做测试，里面有负数，有正数
input = torch.tensor([[1,-0.5],
                      [-1,3]])

#接下来就可以用ReLU这个非线性激活函数了，帮助我们对这个图像进行一个具体理解。
#但是在使用这个函数的时候，我们发现要求的input需要知道batchsize，所以接下来进行此操作。 
#第一个-1代表想让它自己计算这个batchsize；
#第二个1因为我们只有一层，所以它的channel值1；
#第三四个2是2*2的意思。
input = torch.reshape(input,(-1,1,2,2)) 
print(input.shape)

#接下来就可以写我们的神经网络了   
class Feihan(nn.module)：
      def __init__(self)：
          super(Feihan,self).__init__()
          #一般使用这个函数需要在前面导入一下：from torch.nn import ReLU
          #我们会发现括号里的参数是inplace,它的意思是我们是否在原来位置上进行一个替换（即会不会对原来的变量进行一个结果的替换），具体可借助图十九进行具体的理解。一般情况下我们建议将其设置为False,因为这样的话你可以保留一个自己的原始数据，防止数据的丢失。同时它的默认值也为False,所以我们在这里可以不管它，也就是不用对它进行一个设置，下面的参数括号里可以为空。
          self.relu1 = ReLU()

      def forward(self,input):
          #对input进行一个非线性激活
          output = self.relu1(input)
          return output

#初始化这个网络
feihan = Feihan()
output = feihan(input)
print(output)
#输出结果为：tensor([[[[1.,0.],
#                    [0.,3.]]]])
#我们可以看到当input（输入）>=0的时候，output（输出）就取input的原始值，input（输入）<=0,output（输出）就会被截断，全部取为0。

图十九：
还有一个非线性激活方法是Sigmoid，它的具体图像如图二十所示，它是根据图二十上面的那个公式进行计算得到的值，它和上面Relu一样只需要知道input的batchsize即可，别的输入数据的参数都不用知道。
图二十：

一个实例进行具体理解：
nn_Sigmoid.py

#对Sigmoid非线性激活方法进行一个具体的理解
#这个实例数据集的选取，我们就拿torchvision下的CIFAR（CIFAR10）这个数据集来进行一个输入
import torch
from torch import nn
from torch.nn import Sigmoid
from torch.utils.data import DataLoader
from torch.utils.ensorboard import SummaryWriter
import torchvision

#获取数据集
dataset = torchvision.datasets.CIFAR10(root="./dataset",train=False,transform=torchvision.transforms.ToTensor(),download=True)
#加载数据到神经网络中去
dataloader = Dataloader(dataset,batch_size=64)

#接下来就可以写我们的神经网络了   
class Feihan(nn.module)：
      def __init__(self)：
          super(Feihan,self).__init__()
          self.sigmoid1 = Sigmoid

      def forward(self,input):
          #对input进行一个非线性激活
          output = self.Sigmoid1(input)
          return output

#初始化这个网络
feihan = Feihan()

#如果想要比较直观的显示则需要使用Tensorboard
writer = SummaryWrite("logs")
step = 0

for data in dataloader:
     imgs,targets = data
     writer.add_images("input",imgs,step)
     output = feihan(imgs)
     writer.add_images("output",output,step)
     step = step + 1
writer.close()

3.4 线性层

线性层(Linear Layers)： 如图二十一所示，采用的就是一个线性连接的方式。图中的X1、X2…Xd的个数就是线性层中的in_features，即这里X1到Xd是d个，则in_features应该设置为d ；图中的g1、g2…gL的个数就是线性层中的out_features，即这里g1到gL是L个，则out_features应该设置为L。如何从X1、X2…Xd这一层计算出到g1、g2…gL这一层的每个对应的值呢？其实它们两层之间的箭头上面有一个都有一个计算公式，类似于：K1X1+b1、K2X2+b2…(这里的K其实就是线性层里的weight；这里的b是偏置bias，至于加不加b，是由线性层中的bias来决定的:如果将bias设置为True就会加b，如果设置为False就不加b)(神经网络训练过程中就会对这里的K和b做一个调整，以达到一个比较合理的预测)。这就相当于一个线性网络。
图二十一：
我们接下来通过如图二十二所示的vgg16这个典型的网络结构进行一个理解，它涉及到的线性层是我们用黄框圈出来的部分。一开始这个数据是114096，通过线性层的处理就变成了111000（所以这里的in_features是4096，out_features是1000)。
图二十二:

一个实例进行具体理解：
比如：图二十三所示有一张55的图片，现在我们想把这个55的图片展成一行（也就是展成1*25的格式），然后我们想把这25个数据通过线性层最后变成3个。
图二十三：
一个类似于上面实例过程的具体代码如下所示：
nn_linear.py

#对线性层进行一个具体的理解
#这个实例数据集的选取，我们就拿torchvision下的CIFAR（CIFAR10）这个数据集来进行一个输入
import torch
from torch import nn
from torch.utils.data import DataLoader
from torch.utils.ensorboard import SummaryWriter
import torchvision
from torch.nn import Linear

#获取数据集
dataset = torchvision.datasets.CIFAR10(root="./dataset",train=False,transform=torchvision.transforms.ToTensor(),download=True)
#加载数据到神经网络中去
dataloader = Dataloader(dataset,batch_size=64)

#接下来就可以写我们的神经网络了 
class Feihan(nn.module)：
      def __init__(self)：
          super(Feihan,self).__init__()
          #这里使用到Linear，下面是Linear中的一些参数定义：
             #in_features：输入数据的个数，这里的196608是我们通过output = torch.reshape(imgs,(1,1,1,-1)) 算出来的。
             #out_features：输出数据的个数，此时我们把它人为的设置为10。
             #bias：决定是否设置偏置，如果将其设置为True就说明要设置偏置，如果设置为False就说明不要设置偏置。默认情况下取的是True。
          self.linear1 = Linear(196608,10)

      def forward(self,input):
          #对input进行一个线性处理
          output = self.linear1(input)
          return output
          
#初始化这个网络
feihan = Feihan()

for data in dataloader:
     imgs,targets = data
     #此步目的是为了查看数据集中图片的格式
     #我们发现运行结果是torch.Size([64,3,32,32])
     print(imgs.shape)
  
     #但此时我们想把数据集中图片的格式改为torch.Size([1,1,1, ])的形式
     #变换为这种格式以后，我们并不知道最后一个空的具体数值，所以我们可以把它写出-1，交给计算机自己去算即可
     #output = torch.reshape(imgs,(1,1,1,-1)) 
     #我们发现此时运行结果是torch.Size([1,1,1,196608])
     #此时说明我们已经成功将我们数据集中图片的格式改为我们想要的格式了
     
     #torch.flatten这个函数的意思是把数据摊平的意思，也就是类似于图二十三中第一步到第二步的变换,即图二十三所示有一张5*5的图片，现在我们想把这个5*5的图片摊平成一行（也就是展成1*25的格式）。
     output = torch.flatten(imgs)
     print(output.shape)
     #此时运行结果是torch.Size([196608]),它就直接把前面的三个1给省略了

     #经过线性层以后数据变成了torch.Size([1,1,1,10])这种格式
     #如果此时用的是flatten这个函数进行实现的，则运行结果直接为torch.Size([10]),也就直接把前面的三个1给省略了
     output = feihan(output)
     print(output.shape)

其他层还有： Normalization Layers（正则化层）、Recurrent Layers、Transformer Layers、Dropout Layers、Sparse Layers等。

4 神经网络小实战

神经网络-小实战：
这里我们写一下对torchvision下的CIFAR（CIFAR10）这个数据集来进行一个分类的简单神经网络。
如图二十四所示是CIFAR10的一个简单的网络（模型）结构，我们会发现它很简单，也没有加一些非线性特征什么的，具体过程如下所示：

1. 我们可以看到input(输入)是一个3通道的3232的图片，然后它经过一个55（即kernel_size=5）的卷积核进行一个卷积，然后它就变成了一个32通道的32*32的特征图片。
2. 接着它通过一个22（即kernel_size=2）的池化核进行一个池化，很明显看到它的尺寸进行了减半，然后它就变成了一个32通道的1616的特征图片。
3. 接着它再经过一个55（即kernel_size=5）的卷积核进行一个卷积，然后它就变成了一个32通道的1616的特征图片。
4. 接着它再通过一个22（即kernel_size=2）的池化核进行一个池化，很明显又看到它的尺寸进行了减半，然后它就变成了一个32通道的88的特征图片。
5. 接着它再经过一个55（即kernel_size=5）的卷积核进行一个卷积，然后它就变成了一个64通道的88的特征图片。
6. 接着它再通过一个22（即kernel_size=2）的池化核进行一个池化，很明显又看到它的尺寸进行了减半，然后它就变成了一个32通道的44的特征图片。
7. 接着把它进行了展平，展成了一行，它就有6444这么多个
8. 接着它通过了一个线性层，把线性的out_features设置为了64，也就是图上倒数第二个模块Fully connected。
9. 接着它通过了一个线性层，把线性的out_features设置为了10，也就是图上最后的Outputs。

图二十四：

我们将上面的过程（即这个模型）用代码表示，则如下所示：
nn_seq.py

from torch import nn
from torch.nn import Conv2d,MaxPool2d,Flatten,Linear,Sequential
import torch
from torch.utils.ensorboard import SummaryWriter

#我们先写这个网络模型
class Feihan(nn.module)：
      def __init__(self)：
          super(Feihan,self).__init__()
          #卷积
          #这里我们可以由图直接得到前三个参数的数值，即in_channels、out_channels、kernel_size，但不知道后两个参数的数值（stride和padding），所以就需要我们根据公式来进行计算一下了
          #计算公式如图二十五所示：我们将Hout=32,Hin=32,kernel_size=5,dilation采用默认的1（这里没有说它用的是空洞卷积，所以采用的就是一个默认值1，就是没有采用空洞卷积。一定要注意这个dilation比较特殊，虽然你觉得1它是一个空洞卷积，但其实它不是）进行一个带入,可以得到（32+2*padding-4-1）/stride=31，即（27+2*padding）/stride=31。
          #我们发现可以将padding设置为2，stride设置为1的时候刚好满足上面这个式子的结果31。
          #因为如果将stride设置为1的时，上面的（27+2*padding）这部分式子的结果就要拓展的很大，导致padding设置的很大，这样很不合理。
          #所以stride=1,padding=2就是我们最后的一个结果
          self.conv1 = Conv2d(3,32,5,stride=1,padding=2)
          #池化
          self.maxpool1 = MaxPool2d(2)
          #卷积
          #这里stride和padding的数值也需要进行一个计算，具体方法和前面一样
          self.conv2 = Conv2d(32,32,5,stride=1,padding=2)
          #池化
          self.maxpool2 = MaxPool2d(2)
          #卷积
          #这里stride和padding的数值也需要进行一个计算，具体方法和前面一样
          self.conv3 = Conv2d(32,64,5,stride=1,padding=2)
          #池化
          self.maxpool3 = MaxPool2d(2)
          #展平
          self.flatten = Flatten()
          #第一个线性层
          self.linear1 = Linear(1024,64)
          #第二个线性层
          #这里的out_features为什么取10呢？是因为它是要分成十个类别。如果预测的是概率的话则去这是个里面最大的对应的类别,那么就是这个图片经过网络预测预测到的一个类别。
          self.linear2 = Linear(64,10)

          #这里我们简单的在了解一下Sequential，它括号里写的是我们的网络结构
          #self.model1 = Sequential(
              #Conv2d(3,32,5,stride=1,padding=2),
              #MaxPool2d(2),
              #Conv2d(32,32,5,stride=1,padding=2),
              #MaxPool2d(2),
              #Conv2d(32,64,5,stride=1,padding=2),
              #MaxPool2d(2),
              #Flatten(),
              #Linear(1024,64),
              #Linear(64,10)
          )
          
     def forward(self,x):
          x = self.conv1(x)
          x = self.maxpool1(x)
          x = self.conv2(x)
          x = self.maxpool2(x)
          x = self.conv3(x)
          x = self.maxpool3(x)
          x = self.flatten(x)
          x = self.linear1(x)
          x = self.linear2(x)
          return x

          #通过Sequential写网络结构的时候，我们在forward函数里面写的格式如下：
          #x = self.model1 (x)
          #return x
          #这样的话代码会更加简洁

#初始化这个网络
feihan = Feihan()
print(feihan)

#创建一个假想的输入,假设都是1。[64,3,32,32]是图片的一个规格。
input = torch.ones([64,3,32,32])
#想让它经过一下这个网络
output = feihan(input)
print(output.shape)

#除了上面print这种形式，我们Tensorboard也可以进行一个可视化的
writer = SummaryWrite("logs")
#计算图
#这里的input就是上面自己创建的那一个input,input = torch.ones([64,3,32,32])
writer.add_graph(feihan,input)
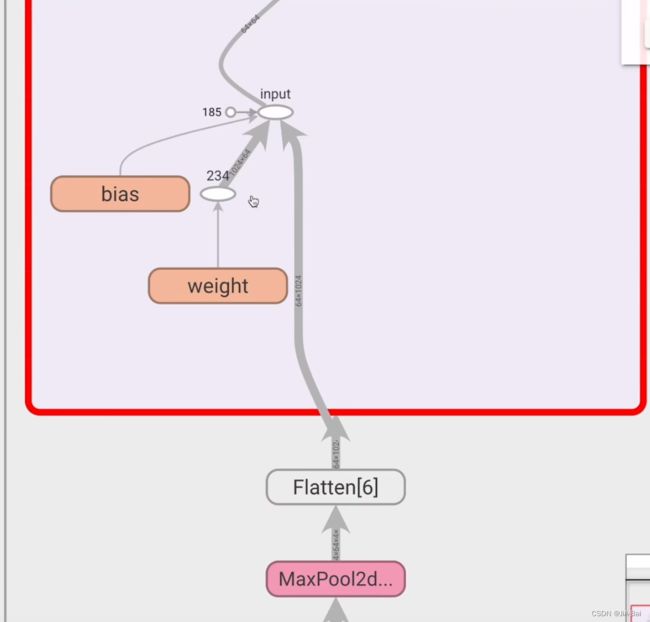
#运行结结果如图二十六所示，它可以进行一层一层的点开，点开结果如图二十七、图二十八、图二十九所示，用来帮助我们对神经网络进行一个更形象的理解
writer.close()

图二十五：
图二十六：

图二十七：

图二十八：

图二十九：