面试官：为什么有了平衡二叉树，还要选择红黑树这种数据结构？

首先讲解为什么要使用红黑树之前，有必要先了解二叉查找树和平衡二叉树，然后继续介绍红黑树，带着这个问题，让我们一起来学习今天的内容吧。

二叉查找树

二叉查找树的特点就是左子树的节点值比父亲节点小，而右子树的节点值比父亲节点大，如下图：

二叉查找树中对于目标节点的查找过程类似于有序数组的二分查找，快速找到某个节点。n 个节点的二叉查找树，正常的情况下，查找的时间复杂度为 O（logn）。

为什么说是正常的情况下呢？

是因为二叉查找树有一种极端的存在，二叉树的大部分子节点都比父节点值小，然后导致所有的数据偏向左侧，进而退化成链表，如下图所示：

这种情况下也是可以满足二叉查找树的条件，但是，此时的二叉查找树已经近似退化为一条链表，这样的二叉查找树的查找时间复杂度顿时变成了 O(n)，所以，为了解决二叉查找树退化为单链表时查找效率低下的问题，引入了平衡二叉树。

平衡二叉树

平衡二叉树，又被称为 AVL 树，是为了解决二叉树退化成一棵链表而诞生的。

平衡二叉树的性质如下：

• 父节点的左右两棵子树的深度之差的绝对值不超过1

从平衡二叉树的性质可知，平衡二叉树就是避免了二叉查找树退化为单链表的极端情况。二叉查找树的查找、插入、删除较好时间复杂度是O(log n)，最差是O(n)。二叉平衡树保证查找、插入、删除的时间复杂度稳定在O(log n)下。

其中左右子树的高度差是通过左旋右旋实现的。

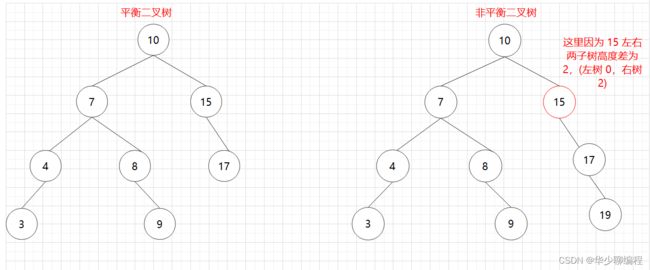
下面是平衡二叉树和非平衡二叉树的图：

左图是一棵平衡二叉树，根节点 10，左右两子树的高度差是 1，而右图，虽然根节点左右两子树高度差是 0，但是右子树 15 的左右子树高度差为 2，不符合定义，所以右图不是一棵平衡二叉树。

虽然平衡树解决了二叉查找树退化为近似链表的缺点，能够把查找时间控制在 O(logn)，不过却不是最佳的，因为平衡二叉树这种高度差绝对值不超过 1 的要求太严格了，在构建一棵平衡二叉树的过程中，当有新的节点要插入时，检查是否因插入后而破坏了树的平衡，如果是，则需要做旋转去改变树的结构，使之再次成为一颗符合要求的平衡树，旋转的作用就是避免出现节点偏向一边的情况，这里的旋转就不在讲了，不是这重点说的。

显然，如果在那种插入、删除很频繁的场景中，平衡树需要频繁着进行调整，这会使平衡树的性能大打折扣，为了解决这个问题，于是有了红黑树。

红黑树（R-B Tree）

红黑树（全称 Red-Black Tree），它是一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

红黑树有如下的特性：

• 每个节点只有两种颜色：红色和黑色
• 根节点是黑色的
• 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存数据
• 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的
• 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点

红黑树示意图如下：

正是由于红黑树的这种特点，使得它能够在最坏情况下，也能在 O(logn) 的时间复杂度查找到某个节点。但与平衡树不同的是，红黑树在插入、删除等操作，不会像平衡树那样，频繁着破坏红黑树的规则，所以不需要频繁着调整。意思是查找效率相当，但是插入、删除效率高于平衡树，这也是我们为什么大多数情况下使用红黑树的原因。

但是需要注意的是，如果应用场景中对插入、删除不频繁，只是对查找要求较高，那么平衡二叉树还是较优于红黑树的。

好了，以上就是为什么需要使用红黑树的原因。

要想了解更多红黑树的相关知识，请看我这篇文章：图解红黑树的前世今生