C++ 数据结构 栈 中缀表达式转后缀表达式并求值

写在前面，这里用的是我自己写的Stack类，并非STL，实现方法为静态数组，但使用过程中的函数方法一样，无伤大雅。（完整code和Stack_static类赋在最后）

中缀表达式转后缀表达式：

1.从左到右遍历

2.数，即参与运算数，直接放进后缀表达式之后

3.左括号，直接压入栈（因为括号的优先级最高，无需判断）（入栈后优先级最低，确保其它的符号正常入栈）

4.右括号,意味着括号已经结束，那么不断弹出栈顶，直到遇到左括号。

5.运算符,将该运算符与栈顶运算符进行比较

        如果优先级高于栈顶运算符则压入堆栈

        如果优先级低于或等于栈顶运算符则将栈顶运算符弹出并放入后缀表达式中

        ***这里是核心，低于或等于栈顶元素意味着前面部分可以运算了，先放入表达式，即先进行运算的一定是高优先级的运算符。

        直到优先级大于栈顶运算符或者栈空，再将该运算符入栈。

6.对字符串处理完毕后，则按顺序弹出栈中所剩运算符，放入表达式中

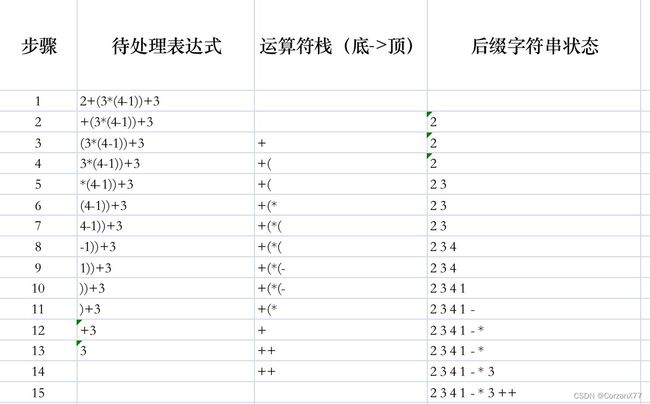
这里我给出一个例子：2+(3*(4-1))+3

code中的栈类是我自己写的类，不是STL中的，但功能大致一样，

/*
返回运算符的优先级
*/
int value(char c){
    switch(c){
        case '(':
            return 0;
            break;
        case '+':
        case '-':
            return 1;
            break;
        case '*':
        case '/':
            return 2;
            break;
        default:
            cout<<"input error"<='0' && str[i]<='9'){//若为数字，则直接接到后缀表达式后面
            changed += str[i];
            opflag = 0;
        }
        else if(str[i]=='('){//若为左括号，直接压入栈
            s.push(str[i]);
        }
        else if(str[i]==')'){//若为右括号，一直出栈接入后缀表达式，直到遇到左括号
            while(s.top()!='('){
                changed += ' ';
                changed += s.top();
                s.pop();
                if(s.empty())break;
            }
            s.pop();
        }
        else{
            if(opflag){
                changed += str[i];
                opflag = 0;
            }
            else{
                changed += ' ';//遇到正常的符号，说明一个数字已经输入完毕，所以加一个空格隔开个个数字
                if(s.empty())s.push(str[i]);//若栈空，则直接入栈
                else if(value(str[i]) > value(s.top()))s.push(str[i]);//若优先级大于栈顶，直接入栈
                else {//若优先级小于等于前一个，则不断比较并出栈
                    while(value(str[i]) <= value(s.top())){
                        changed += s.top();
                        changed += ' ';
                        s.pop();
                        if(s.empty())break;//如果空了，退出循环
                    }
                    s.push(str[i]);
                }
                opflag = 1;
            }
        }
    }
    while(!s.empty()){//当结束时，栈不为空，则一个一个出栈
        changed += ' ';
        changed += s.top();
        s.pop();
    }
    return changed;//返回最终的后缀表达式
}

接下来是后缀表达式的求值方法

1.依旧是从左到右遍历字符串

2.数，这次的数的处理是直接压入栈

3.符号，若是空格，则将前面保存的数压入栈（因为数可能是多位数，所以不能直接压入栈，有别于转后缀。所以我们需要一个数来保存字符输进来的数字。）

4.运算符，碰到一个运算符，我们就进行一次计算，对栈顶的两个数字进行计算，这也就是后缀表达式的计算原理

接下来举个例子，式子与上面的相同

后缀表达式为2 3 4 1-* 3++

最后所剩的14即为最终答案，直接输出即可

下面是实现的代码

//计算两个数，用于弹出的运算符和两个数
double calculate(double x,double y,char c){
    switch (c)
    {
    case '+':
        return x+y;
        break;
    case '-':
        return x-y;
        break;
    case '*':
        return x*y;
        break;
    case '/':
        if(!y){
            cerr<<"除数不能为0"<='0' && str[i]<='9'){//遇到数字存入num中
            num = num*10 + str[i]-'0';
            flag = 1;//flag用来记录现在数字是否存在
        }
        else{
            if(flag){//避免连续读入字符时，数字栈中存入多个0
                if(fu_flag)//如果是负数
                    S_num.push(-double(num));
                else
                    S_num.push(double(num));
                flag = 0;
                fu_flag = 0;
                num = 0;//置0
            }
            if(str[i]==' '){
                fu_flag = 0;
                continue;
            }
            if(str[i]=='-' && str[i+1]>='0' && str[i+1]<='9'){
                fu_flag = 1;
                continue;
            }
            
            double a,b;
            a = S_num.top();//取出栈顶
            S_num.pop();
            b = S_num.top();//取出栈顶
            S_num.pop();
            S_num.push(calculate(b,a,str[i]));//计算后压入栈
        }
    }
    return S_num.top();
}

我的Stack_static类，是静态数组的实现

#include
const int STACK_MAX = 128;
typedef int StackElement;
class Stack_static
{
private:
    StackElement myArray[STACK_MAX];
    int myTop;
public:
    Stack_static();
    ~Stack_static();
    void push(const StackElement &value);
    void pop();
    StackElement top();
    bool empty();
    void display(std::ostream & out);
    int get_myTop(){
        return myTop;
    }
    StackElement bottom();
};

Stack_static::Stack_static()
{
    myTop = -1;
}

Stack_static::~Stack_static()
{
}

bool Stack_static::empty(){
    if(myTop==-1)return true;
    return false;
}

StackElement Stack_static::top(){
    if( !empty())
        return myArray[myTop];
    else{
        std::cerr << "*** Stack is empty -- return ***\n";
        StackElement garbage=0;
        return garbage;
    }
}

void Stack_static::push(const StackElement &value){
    if(myTop < STACK_MAX-1){
        myTop++;
        myArray[myTop] = value;
    }
    else{
        std::cerr << "*** Stack full -- can't add new value ***\n";
        exit(1);
    }
}

void Stack_static::pop(){
    if(!empty())
        myTop--;
    else    
        std::cerr << "*** Stack is empty***\n";
}

void Stack_static::display(std::ostream &out){

    
    for(int i = myTop-1;i >= 0; i-- ){
        out<< myArray[i] << std::endl;
    }
}

StackElement Stack_static::bottom(){
    if(!empty()){
        return myArray[0];
    }
    else{
        std::cerr<<"*** Stack is empty!***\n";
        StackElement garbage=0;
        return garbage;
    }
}

整个代码以及测试：

#include"Stack_static.h"
#include
using namespace std;

//简易计算器，只包含+-*/（）

/*
返回运算符的优先级
*/
int value(char c){
    switch(c){
        case '(':
            return 0;
            break;
        case '+':
        case '-':
            return 1;
            break;
        case '*':
        case '/':
            return 2;
            break;
        default:
            cout<<"input error"<='0' && str[i]<='9'){//若为数字，则直接接到后缀表达式后面
            changed += str[i];
            opflag = 0;
        }
        else if(str[i]=='('){//若为左括号，直接压入栈
            s.push(str[i]);
        }
        else if(str[i]==')'){//若为右括号，一直出栈接入后缀表达式，直到遇到左括号
            while(s.top()!='('){
                changed += ' ';
                changed += s.top();
                s.pop();
                if(s.empty())break;
            }
            s.pop();
        }
        else{
            if(opflag){
                changed += str[i];
                opflag = 0;
            }
            else{
                changed += ' ';//遇到正常的符号，说明一个数字已经输入完毕，所以加一个空格隔开个个数字
                if(s.empty())s.push(str[i]);//若栈空，则直接入栈
                else if(value(str[i]) > value(s.top()))s.push(str[i]);//若优先级大于栈顶，直接入栈
                else {//若优先级小于等于前一个，则不断比较并出栈
                    while(value(str[i]) <= value(s.top())){
                        changed += s.top();
                        changed += ' ';
                        s.pop();
                        if(s.empty())break;//如果空了，退出循环
                    }
                    s.push(str[i]);
                }
                opflag = 1;
            }
        }
    }
    while(!s.empty()){//当结束时，栈不为空，则一个一个出栈
        changed += ' ';
        changed += s.top();
        s.pop();
    }
    return changed;//返回最终的后缀表达式
}

//计算后缀表达式的值
double result(string str){
    Stack_static S_num;
    int num = 0,flag = 0,fu_flag = 0;
    for(int i = 0;i < int(str.length());i++){
        if(str[i]>='0' && str[i]<='9'){//遇到数字存入num中
            num = num*10 + str[i]-'0';
            flag = 1;//flag用来记录现在数字是否存在
        }
        else{
            if(flag){//避免连续读入字符时，数字栈中存入多个0
                if(fu_flag)//如果是负数
                    S_num.push(-double(num));
                else
                    S_num.push(double(num));
                flag = 0;
                fu_flag = 0;
                num = 0;//置0
            }
            if(str[i]==' '){
                fu_flag = 0;
                continue;
            }
            if(str[i]=='-' && str[i+1]>='0' && str[i+1]<='9'){
                fu_flag = 1;
                continue;
            }
            
            double a,b;
            a = S_num.top();//取出栈顶
            S_num.pop();
            b = S_num.top();//取出栈顶
            S_num.pop();
            S_num.push(calculate(b,a,str[i]));//计算后压入栈
        }
    }
    return S_num.top();
}

//测试代码
int main(){
    string a;
    cout << "Infix expression?";
    cin >> a;
    cout << "Postfix expression is " << change(a) << endl;
    cout << "Result:" << result(change(a));
    return 0;
}