深入浅出——网络嵌入算法DeepWalk
DeepWalk是一种利用的截断随机游走获得网络的结构信息,来进行网络嵌入的算法。将网络中的节点嵌入到一个潜在的连续空间中。
一.随机游走
DeepWalk是利用截断随机游走来获取节点的上下文信息(可以认为是网络的局部结构信息)。
随机游走:从一个节点出发,随机选择它的一个邻居节点,接着从这个邻居节点出发到该邻居节点的邻居节点,重复这个步骤直到经过所有节点。
在DeepWalk中是采用截断的方法,提取终止随机游走,得到一个比较短的随机游走序列。提前设置参数 t t t为一次随机游走的长度,达到这个长度就会停止随机游走。另外在游走过程中是会以一定概率回到根节点的,在DeepWalk的论文中只表示存在这种可行性,但是实验并没有表明存在回到根节点的概率会提高模型效果。
这种短距离的随机游走有两个好处:
- 并行性。局部的随机游走,可以在网络的各个部分同时进行。
- 适应性。适应网络结构较小的改变,不需要重新进行全局的计算。只需要在改变的区域进行随机游走,来更新模型
由于DeepWalk游走的方式,DeepWalk只适用于无权图。
二.幂律分布
幂律分布表现为一条斜率为幂指数的负数的直线,这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。
社交网络中的无标度现象也是一种幂律分布。
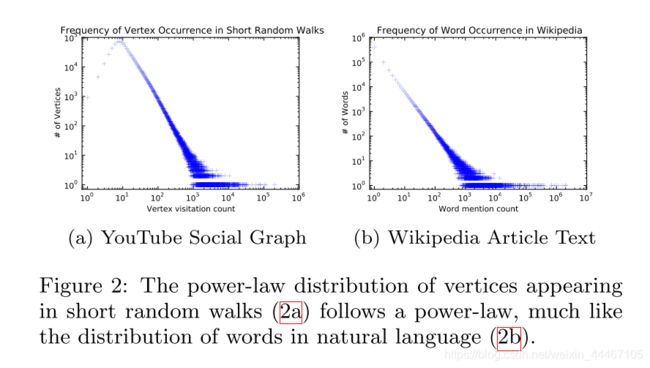
节点的度往往是幂律分布的,那么通过随机游走得到的序列中,节点出现的频率就应该是幂律分布的。
下图就是论文中的图,也证明了随机游走得到的序列,节点出现的次数是服从幂律分布的。
因为自然语言处理的模型是用于幂律分布的单词的,所以也可以用于幂律分布的网络。
三.模型
1.Skip-Gram
在一般的词向量模型中,给点一个单词序列 W = ( w 0 , w 1 , . . . w n ) W=(w_0,w_1,...w_n) W=(w0,w1,...wn),在训练集上的优化目标就变成:
m a x ( P r ( w n ∣ w 0 , w 1 . . . w n − 1 ) ) max (Pr(w_n| w_0,w_1...w_{n-1})) max(Pr(wn∣w0,w1...wn−1))
这里借鉴了skip-gram里的思想(利用缺失值来估计上下文),给点网络中的节点,来最大化随机游走得到的序列中其它节点的共现似然概率。
Skip-gram模型的特点有三个:
- 利用缺失值来预测上下文,而不是用上下文来预测缺失值。应用到网络中就是用节点来估计其邻近节点,而不是用邻近节点来估计其节点
- 同时考虑左右两个窗口,对于 w 2 w_2 w2来说, w 1 w_1 w1和 w 3 w_3 w3都是要考虑的。
- 不考虑顺序,对于 w 2 w_2 w2来说, w 1 w_1 w1和 w 3 w_3 w3都是等价的。
文中将特点3的优点分为了两个部分:(也导致只适用于无向图)
- 更好的体现随机游走中的邻近关系。
- 只需要计算一个顶点的向量,减少了计算量。这里可以理解为算法2中第4行只更新一个用户的表征。
所以目标函数就变成了:
m i n − l o g P r ( v i − w , . . . v i − 1 , v i + 1 , . . . v i + w ∣ v i ) min-log Pr(v_{i-w},...v_{i-1},v_{i+1},...v_{i+w}|v_i) min−logPr(vi−w,...vi−1,vi+1,...vi+w∣vi)
2.算法流程
算法主要分为两个部分:随机游走序列的生成,参数更新。
算法1为DeepWalk的整体算法。

算法2为参数更新部分,这里是借鉴了SkipGram.

3.Hierarchical Softmax
这一部分也是word2vec里面关于单词处理的部分,主要作用是加速计算。将时间复杂度从O(|V|)提高到O(log|V|)
具体实现可以参考之前写的文章https://blog.csdn.net/weixin_44467105/article/details/110926452
4.并行化
这里的并行化是利用了 ‘FASTER ASYNCHRONOUS SGD’ 论文里提出的异步随机梯度下降。这里不详述。
论文:DeepWalk: Online Learning of Social Representations