面试常考排序算法超详细总结
算法基本知识铺垫
有些人可能不知道什么是稳定排序、原地排序、时间复杂度、空间复杂度,我这里先简单解释一下:
1、稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 仍然在 b 的前面,则为稳定排序。
2、非稳定排序:如果 a 原本在 b 的前面,且 a == b,排序之后 a 可能不在 b 的前面,则为非稳定排序。
3、原地排序:原地排序就是指在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储
空间进行比较和交换的数据排序。
4、非原地排序:需要利用额外的数组来辅助排序。
5、时间复杂度:一个算法执行所消耗的时间。
6、空间复杂度:运行完一个算法所需的内存大小
排序中的稳定排序
冒泡排序(bubble sort) — O(n2)
插入排序 (insertion sort)— O(n2)
归并排序 (merge sort)— O(n log n)
排序中的非稳定排序
面试考察中一般问快排,选择,希尔,堆这几种非稳定排序
选择排序 (selection sort)— O(n2)
希尔排序 (shell sort)— O(n log n)
堆排序 (heapsort)— O(n log n)
快速排序 (quicksort)— O(n log n)
冒泡排序:
冒泡排序法的各个计算步骤中, 数组也分成 “已排序部分” 和 “未排序部分”。
冒泡排序法
► 重复执行下述处理,直到数组中不包含顺序相反的相邻元素
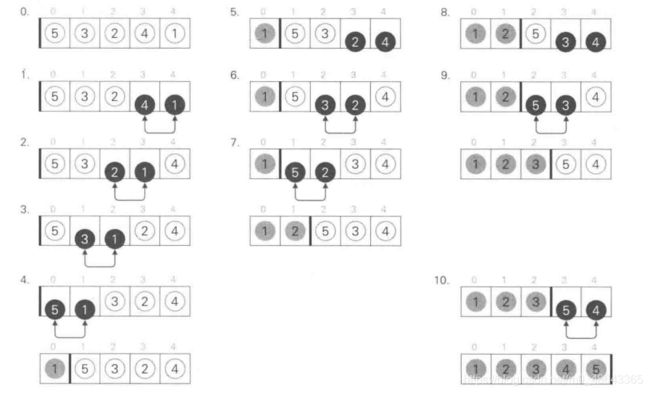
1 . 从数组末尾开始依次比较相邻两个元素,如果大小关系相反则交换位置。
以 数 组 {5,3,2,4, 1 } 为例,我们对其使用冒泡排序法时,排序过程如图下图所示:
代码:
设置标识flag
,用以标识每一趟是否发生了交换,若不发生交换,则说明有序,无需再行比较。这一改进可以避免已经有序情况下无意义的判断。
// 冒泡排序
void bubbleSort(int arr[], int n) {
bool flag = 1;
for (int i = 0; flag; i++) {
flag = 0;
for (int j = n - 1; j >= i + 1; j--) {
if (arr[j] < arr[j - 1]) {
swap(arr[j], arr[j - 1]);
flag = 1;
}
}
}
}
插入排序 :
插入排序法在排序过程中,会将整个数组分成 “已排序部分” 和 “未排序部分”。
插入排序法
► 将开头元素视作已排序
► 执行下述处理,直至未排序部分消失
1.取出未排序部分的开头元素赋给变量v。
2.在已排序部分,将所有比 v 大的元素向后移动一个单位。
3.将已取出的元素 v 插入空位。
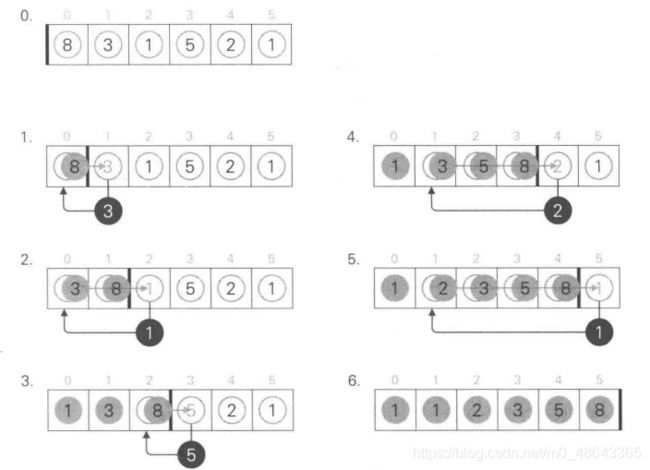
举个例子,我们对数组 {8,3,1,5,2,1 } 进行插入排序时,整体流程如图下图 所示:
代码:
//插入排序
void insertionSort(int arr[], int n) {
int j, v;
for (int i = 0; i < n; i++) {
v = arr[i];
j = i - 1;
while (j >= 0 && arr[j] > v) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = v;
}
}
归并排序 :
在一些体积庞大的数组面前,胃泡排序等复杂度高达 0(n^2)的初等排序算法就失去了实用
价值。对付这类数据要用到高等算法,归并排序就是其中之一。
归并排序
► 以整个数组为对象执行 mergeSort
► mergeSort 如下所示
1 . 将给定的包含n个元素的局部数组 “分割” 成两个局部数组,每个数组各包含n/2个元素。( Divide )
2.对两个局部数组分別执行 mergeSort 排序。( Solve )
3.通过 merge 将两个已排序完毕的局部数组 “整合” 成一个数组。( Conquer )
举个例子,我们对数组 {9, 6,7,2,5,1,8,4. 2} 进行归并排序,其过程如图 所示:

- 一般说来,n 个数据大致会分为 log2n层。由于每层执行 merge 的总复杂度为 O(n), 因此归并排序的整体复杂度为O(nlog2n)。
- 归并排序包含不相邻元素之间的比较,但并不会直接交换。在合并两个已排序数组时,如果遇到了相同元素,只要保证前半部分数组优先于后半部分数组,相同元素的顺序就不会颠倒。因此归并排序属于稳定的排序算法。
- 归并排序算法虽然高效且稳定,但它在处理过程中,除了用于保存输入数据的数组之外, 还需要临时占用一部分内存空间。
代码:
//归并排序,先不断的分割区间,至区间只有两个元素,然后在不断地合并子区间
void Mymerge(int arr[],int le,int ri,int ll,int rr){
int temp[1000];int k = 0;
int sta = le,en = rr;
while(le<=ri&&ll<=rr){
if(arr[le]<arr[ll])temp[k++] = arr[le++];
else temp[k++] = arr[ll++];
}
while(le<=ri)temp[k++] = arr[le++];
while(ll<=rr)temp[k++] = arr[ll++];
for(int i = sta;i<=en;i++){
arr[i] = temp[i-sta];
}
}
void mergeSort(int arr[],int le,int ri){
if(le>=ri)return ;
int mid = (le+ri)>>1;
mergeSort(arr,le,mid);
mergeSort(arr,mid+1,ri);
Mymerge(arr,le,mid,mid+1,ri);
}
选择排序 :
与插入排序法和冒泡排序法一样, 选择排序法的各个计算步骤中,数组也分成 “已排序部分” 和 “未排序部分”。
选择排序法
► 重复执行 N-1 次下述处理
1 . 找出未排序部分最小值的位置 minj。
2.将 minj 位置的元素与未排序部分的起始元素交换。
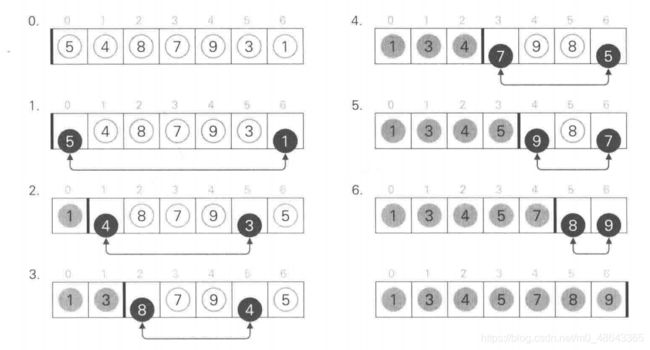
以数组 J ={5,4,8,7,9,3, 为例,我们对其使用选择排序法时,排序过程如图所示:
代码:
//选择排序
void selectionSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
int minj = i;
for (int j = i; j < n; j++) {
if (arr[j] < arr[minj]) minj = j;
}
swap(arr[i], arr[minj]);
}
}
希尔排序:
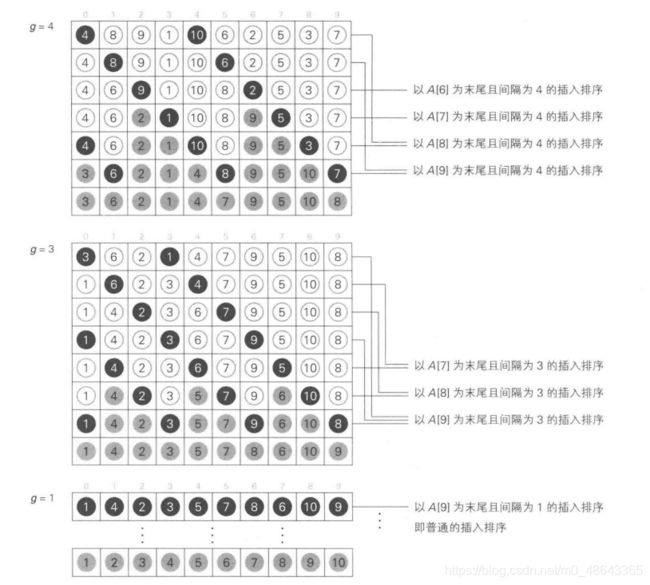
我们之前提到过,插人排序法可以高速处理顺序较整齐的数据,而希尔排序法就是充分发挥插人排序法这一特长的高速算法。希尔排序法中,程序会重复进行以间隔为 g 的元素为对象的插入排序。
举个例子,设g 的集合为 G,对3 = {4,8,9,1,10,6,2,5,3, 7} 进行 G ={4,3,1}的希尔排序,其整体过程如图所示:
代码:
//希尔排序,其实就是插入排序,不过是间隔为D的序列中进行的
void shellInsert(int arr[],int d,int n){
for(int i=d;i<n;i++){
int j = j-d;
int temp = arr[i];
while(j>=0&&arr[j]>temp)
{
arr[j+d] = arr[j];
j -= d;
}
arr[j+d] = temp;
}
}
void ShellSort(int arr[],int n)
{
int d = n/2;
while(d>=1){
shellInsert(arr,d,n);
d/=2;
}
快速排序
快速排序是基于下述分治法的算法
以整个数组为对象执行 quicksort
► quicksort 流程如下
1.通过分割将对象局部数组分割为前后两个局部数组。( Divide )
2.对前半部分的局部数组执行 quicksort。( Solve )
3.对后半部分的局部数组执行 quicksort。( Solve )
快速排序的函数 quicksort 通过分割将局部数组一分为二,然后对前后两组再递归地执行 quicksort , 从而完成给定数组的排序。例子是对A= {13,19,9,5,12,8,7,4,21,2,5,3,14,6,11} 使用快速排序的过程。
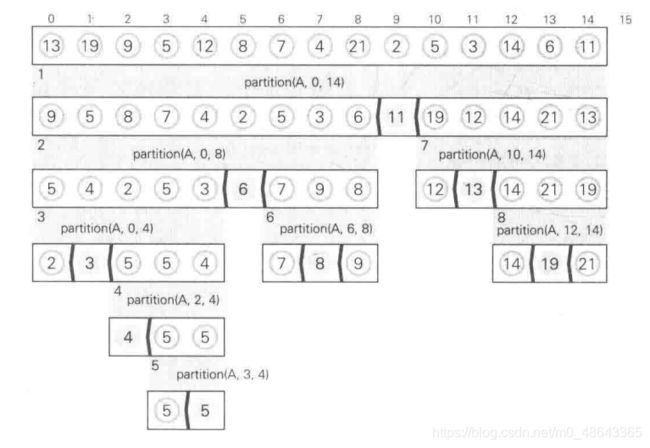
- 快速排序与归并排序一样基于分治法,但其执行 partition 进行分割时就已经在原数组中完成了排序,因此不需要归并排序中那种手动的合并处理。
- 快速排序在分割的过程中会交换不相邻元素, 因此属于不稳定的排序算法。 另一方面,归并排序需要 O(n)的外部存储空间,快速排序则不必额外占用内存也就是说,快速排序是一种原地排序(内部排序)
- 如果快速排序在分割时能恰好选择到中间值,则整个过程与归并排序一样大致分为log2n层。快速排序的平均复杂度为 O(nlog2n),是一般情况下最高效的排序算法。
代码:
方法1:
void quickSort(vector<int>& nums, int begin, int end) {
if (begin >= end) return;
int low = begin, high = end, key = nums[begin];
while (low < high) {
while (low < high && nums[high] >= key) {
high--;
}
if (low < high) nums[low++] = nums[high];
while (low < high && nums[low] <= key) {
low++;
}
if (low < high) nums[high--] = nums[low];
}
nums[low] = key;
quickSort(nums, begin, low - 1);
quickSort(nums, low + 1, end);
}
方法2:
void quicksort(vector<int>& arr, int l, int r) {
if (l>=r) return;
int i = l, j = r;
while (i < j) {
while (i <j && arr[j] >= arr[l]) j--;
while (i < j && arr[i] <= arr[l]) i++;
swap(arr[i], arr[j]);
}
swap(arr[l], arr[i]);
quicksort(arr, l, i - 1);
quicksort(arr, i+1, r);
}
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
代码:
//堆排序,先构建一个最大堆,然后依次交换最大值和数组最末位置的值,保证数组有序。
void heapAdjust(int arr[],int sta,int en)
{
int temp = arr[sta];
for(int i=2*sta+1;i<=en;i++)
{
if(arr[i]<arr[i+1]&&i<en)i++;
if(temp>=arr[i])break;
arr[sta] = arr[i];
sta = i;
}
arr[sta] = temp;
}
void heapSort(int arr[],int n)
{
for(int i = (n)/2;i>=0;i--){
heapAdjust(arr,i,n-1);
}
for(int i=n-1;i>=0;i--){
swap(arr[i],arr[0]);
heapAdjust(arr,0,i-1);
}
}
堆排序基本思想及步骤可见:https://www.cnblogs.com/chengxiao/p/6129630.html