算法设计-贪心算法——最小生成树Prim和Kruskal算法

算法介绍

贪心算法：

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。即通过每次贪最优的情况，直到问题结束，是通过局部最优达到整体最优的解决问题的方法。

问题实例

问题描述：

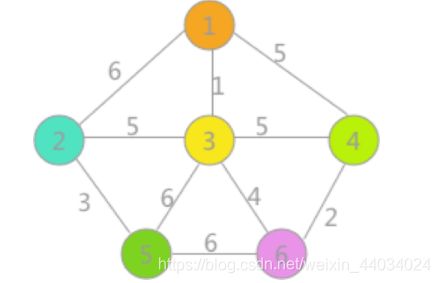
连通带权图G=（V,E) 其中V=｛1，2，3，4，5，6｝，E为10条边的集合，如上图。
请编程求解该图G的一棵最小生成树
分别使用Prim算法和Kruskal算法解决该问题

（一）Prim算法

贪心策略：每次选择到下一顶点权值最小的边
伪代码：
①将所有顶点放入集合V{}中，设最小生成树顶点集S{}。
②将选一点放入S{}中，然后每次选择V-S中离S中顶点最近的顶点加入到S中。
③当V中顶点全都放入S中，结束。
过程如图所示：

代码：

#include 

using namespace std;

#define M 9999
const int N = 6;

void Prim (int n,int **c)
{
    int closest[N+1];// j属于V-S 外，代表closest[j] j离S最近的点
    int lowcost[N+1]; // lowset代表最小的权值 c[i][closet[j]]
    bool s[N+1];     // 代表顶点
    s[1]=true;
    for(int i=2;i<n;i++) //初始化
    {
        closest[i]=1;
        lowcost[i]=c[i][1];
        s[i]=false;
    }
    for (int i = 1; i < n; i++)
	{
		int min = M;
		int j = 1;
		// 找出V-S中使权值最小的顶点j
		for (int k = 2; k <= n; k++)
		{
			if ((lowcost[k] < min) && (!s[k]))
			{
				min = lowcost[k];
				j = k;
			}
		}
		// 找到符合贪心选择方式的边，将顶点j加入到集合S
		cout << closest[j] << "--" << j << endl;
		s[j] = true;

		// 找到一条边后，更新数组closest和lowcost
		for (int k = 2; k <= n; k++)
		{
			if ((c[j][k] < lowcost[k] && (!s[k])))
			{
				lowcost[k] = c[j][k];
				closest[k] = j;
			}
		}
	}

}

int main()
{
    int *c[N+1];
    for(int i=0;i<N+1;i++)
    {
        c[i]=new int[N+1];
    }
    int b[N+1][N+1]=
    {
        {M,	M,	M,	M,	M,	M,	M},
		{M,	M,	6,	1,	5,	M,	M},
		{M,	6,	M,	5,	M,	3,	M},
		{M,	1,	5,	M,	5,	6,	4},
		{M,	5,	M,	5,	M,	M,	2},
		{M,	M,	3,	6,	M,	M,	6},
		{M,	M,	M,	4,	2,	6,	M}
    };
    for(int i=0;i<N+1;i++)
    {
        for(int j=0;j<N+1;j++)
        {
            c[i][j]=b[i][j];
        }
    }
    for(int i=0;i<N+1;i++)
    {
        for(int j=0;j<N+1;j++)
        {
            cout<<c[i][j]<<"      ";
        }
        cout<<endl;
    }

    cout<<"Prim最小生成树次序:"<<endl;
    Prim(N,c);
    return 0;

}

结果：

解决该问题的关键是用两个数组分别存储与S{}离得最近的顶点和该顶点的权值，每次将该点加入到S{}中，并通过判断距离决定是否需要更新。

（二）Kruskal 算法

贪心策略：每次贪权值最小并且不会与已经加入的顶点形成回路的边
伪代码：
①先将n个不同顶点赋予不同的颜色进行标记
②利用循环，找到最小的边，判断该边连接的顶点颜色是否相同，如果不同加入到最小生成树中，将这条边连接的两个顶点赋予相同的颜色，如果相同，舍弃该边，继续寻找。
③当找到n-1条边加入到最小生成树中后，结束。
过程如图所示：

将顶点标记不同颜色

找到不同顶点颜色的最小边加入最小生成树，并赋予相同颜色

重复该过程


再次找到颜色不同顶点的最短边时，注意是要将相连所有顶点颜色统一。


代码：

#include 

using namespace std;

#define M 9999
const int N = 6;

void Cx (int b,int z,int *jl)
{
    for(int i=1;i<=N;i++)
    {
        if(jl[i]==z)
        {
            jl[i]=b;
        }
    }
}

void Kruskal (int **a,int *jl)
{
    int Min=M;
    int x,y;
    for(int i=1;i<=N;i++)
    {
        for(int j=i;j<=N;j++)
        {
            if(a[i][j]<Min)
            {
                Min=a[i][j];
                x=i;
                y=j;
            }
        }
    }



    if(jl[x]!=jl[y])
    {

        Cx(jl[x],jl[y],jl);
        jl[y]=jl[x];
        a[x][y]=M;
        cout<<x<<"--"<<y<<" "<<Min<<endl;

    }
    else
    {
        a[x][y]=M;
        Kruskal (a,jl);


    }







}

int main()
{
    int *a[N+1];
    for(int i=0;i<N+1;i++)
    {
        a[i]=new int[N+1];
    }
    int b[N+1][N+1]=
    {
        {M,	M,	M,	M,	M,	M,	M},
		{M,	M,	6,	1,	5,	M,	M},
		{M,	6,	M,	5,	M,	3,	M},
		{M,	1,	5,	M,	5,	6,	4},
		{M,	5,	M,	5,	M,	M,	2},
		{M,	M,	3,	6,	M,	M,	6},
		{M,	M,	M,	4,	2,	6,	M}
    };
    for(int i=0;i<N+1;i++)
    {
        for(int j=0;j<N+1;j++)
        {
            a[i][j]=b[i][j];
        }
    }
    int jl[N+1];
    for(int i=0;i<N+1;i++)
    {
        jl[i]=i;
    }
    cout<<"Kruskal最小生成树次序:"<<endl;
    for(int i=1;i<N;i++)
    {
        Kruskal(a,jl);
    }
    cout<<endl;


}

结果：

解决该问题的关键是如何判断选择出来的最短边是最合适的，即该边不会与已选择的顶点形成回路。我采用的是用不同整数标记顶点的方式，只有当两顶点标记的数字不同时才可加入，即不会形成回路。（原理就是形成回路的起始点和终点会被判断两次）

记录整理一些学习中的问题，如果有不恰当和错误的地方，欢迎批评指正~