一篇文章带你搞懂动态规划问题

前言

这篇博客主要是跟大家相互交流学习动态规划问题，下面记录的是一些我的学习心得。有不足的情况还望大家私聊交流指正。

我写这篇博客的思路大概是这样：首先解释下动态规划的关键概念，然后列出各种动态规划类型的题目，只要能够跟着我的博客完成之后的动态规划题目我觉得应该能够解决平时遇到的百分之90的动态规划的问题

一、动态规划的四大组成部分

1、确定状态

状态在动态规划中的作用至关重要。简单理解状态就是我们需要一个数组，数组中的每个元素就是代表状态。确定状态需要两个关键意识：最后一步和子问题。

（1）最后一步（可以直接根据问题来确定最后一步）

确定最后一步有两个关键点。这里我举个例子，例如常见的零钱兑换问题（你有三种硬币，分别是面值2元，5元，7元的，每种硬币足够多，买一本书需要27元，如何用最少的硬币组合正好付清）。我们不知道这个最优策略是啥，但是可以确定一定有最后的一枚硬币ak，除掉这枚硬币前面的币值加起来就是27-ak，我们不需要去关心前面的k-1枚硬币怎么拼出27-ak的，因为那就是我们的子问题。

（2）子问题

愿问题是用最少的硬币拼出27，而经过刚刚最后一步的确认，我们转化成了如何用最少的硬币拼出27-ak,这就是我们的子问题

确定好了最后一步和子问题，我们就可以开一个数组f[x]表示最少用多少枚硬币拼出X

2、转移方程

通过对最后一步和子问题的确认，我们了解到只需要用最少的硬币拼出27-ak，就可以用最少的硬币拼出27了。而针对ak的选择有三个：2，5，7。因此我们的专业方程就是：

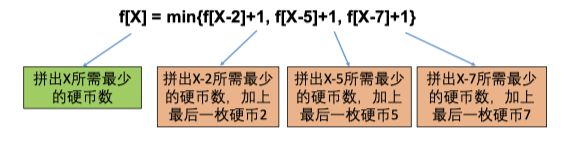
3、初始条件和边界情况

这两个问题就根据字面意思去理解，针对不同的问题看情况而定。比如针对零钱兑换。

初始条件：x=0的时候应该是设置f[x]=多少，很明显f[0]=0

边界情况：x-2，x-5,x-7小于0和不能拼出X的时候该怎么设置，因为我们是求最小值，因此都设置为正无穷。

4、计算顺序

当我们计算f[x]的时候需要知道f[x-2],f[x-5],f[x-7]的值，因此我们计算顺序就是f[0]到f[x]

二、动态规划题目的特点

1、计数

一般技术类型的题目都可以用动态规划解决，例如下面两种类型

• 有多少种方式走到右下角
• 有多少方式选出K个数使得和是Sum

2、求最大值最小值

这种动态规划中最常见的类型，例如

• 从左上角走到右下角路径的最大数字和
• 最长上升子序列长度

3、求存在性

这种问题其实与上面两种类型相互对应，例如

• 取石子游戏，先手是否必胜
• 能不能取出K个数使得和是Sum

三、动态规划题目类型

下面的题目全都来自leetcode或者lintcode，我只是列出了我做过的题目，网站上面还有很多其他动态规划的题目，大家就自行实践。

1、坐标型动态规划

该类型的动态规划是所有类型中最简单的类型。一般题目都是给定一个序列或者一个网格，需要你去找到序列或网格中的某条路径满足最大最小或者进行计数或者判断是否存在。

特点：该类型的题目的特点就是转移方程中的f[i]中的下表i表示以ai结尾的满足条件的子序列的性质。f[i][j]中的下标i，j表示以格子i,j结尾的满足条件的路径的性质。

初始条件：该类型动态规划初始条件f[0]就是以a0结尾的子序列的性质。

64、最小路径和

361、轰炸敌人

2、位操作型动态规划

该类型的题目主要就是指二进制的位操作，分为与，或，异或，非。下面举了个典型的例题

338、比特位计数

3、序列型动态规划

给定一个题目，动态规划方程中f[i]中的下标i表示前i个元素a[0]，a[1]……a[i-1]等的某种性质,注意与坐标类型的动态规划进行区别，其表示以a[i]结尾的某种性质。初始化的时候，f[0]表示空序列的性质。

序列类型的动态规划题目变种非常多，很多题目的代码实现可以完全使用坐标类型动态规划解决问题，所以我的部分题目的代码使用的是坐标类型实现，但是过程分析采用的是序列类型的动态规划思想，大家可以自己尝试实现部分序列类型方法实现的代码

62、不同路径

256、粉刷房子

198、打家劫舍

215、打家劫舍2

300、最长递增子序列

354、俄罗斯套娃信封问题

4、划分型动态规划

该类型的题目给定长度为N的序列或字符串，要求划分成若干段

– 段数不限，或指定K段

– 每一段满足一定的性质

做法

– 类似于序列型动态规划，但是通常要加上段数信息

– 一般用f[i][j]记录前i个元素(元素0~i-1)分成j段的性质，如最小代价

91、解码方法

132、分割回文串2

279、完全平方数

437、书籍复印

5、博弈型动态规划

394、硬币排成线

6、背包型动态规划

该类型的题目是你有一个背包，背包有最大承重，每个物品有重量和价值

目标：不撑爆背包的前提下

– 装下最多重量物品

– 装下最大总价值的物品

– 有多少种方式正好带走满满一书包物品

解决问题的两个关键点：

– 还有 几个物品

– 还剩多少承重

92、背包问题1

125、背包问题2

440、背包问题3

563、背包问题5

564、背包问题6

322、零钱兑换

7、区间型动态规划

该类型的题目，给定一个序列/字符串，进行一些操作

• 最后一步会将序列/字符串去头/去尾

• 剩下的会是一个区间[i, j]

• 状态自然定义为f[i][j]，表示面对子序列[i, …, j]时的最优性质

486、预测赢家

516、最长回文子序列

8、双序列型动态规划

该类型的题目顾名思义，有两个序列/字符串，需要进行一些操作

• 每个序列本身是一维的

• 可以转化为二维动态规划

72、编辑距离

97、交错字符

115、不同的子序列

1143、最长公共子序列