AVL平衡树（Java实现）

概念

AVL树可以定义为高度平衡二叉搜索树，其中每个节点与平衡因子相关联，该平衡因子通过从其左子树的子树中减去其右子树的高度来计算。AVL树是由GM Adelson - Velsky和EM Landis于1962年发明的。为了纪念其发明者，这树结构被命名为AVL。
定义： 任意节点左右子树相差高度不超过1的树

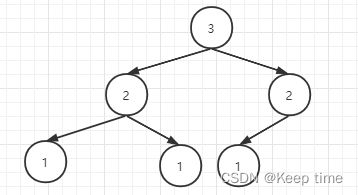
优点： 查找、插入和删除在平均和最坏情况下的时间复杂度都是O(nlogn)

过程

增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡

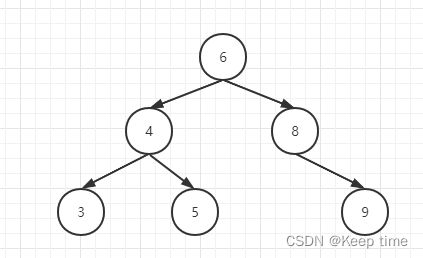
左旋（RR）

插入的元素在不平衡的节点的右侧的右侧
要插入9

（1）节点的右孩子替代此节点位置 （2）右孩子的左子树变为该节点的右子树 （3）节点本身变为右孩子的左子树

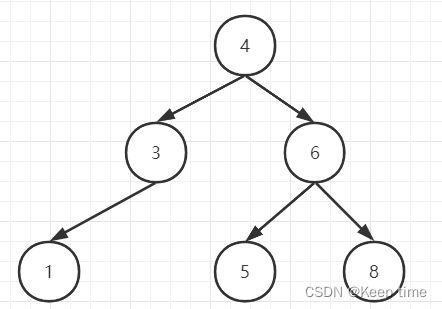
右旋（LL）

插入的元素在不平衡结点的左侧的左侧
现需插入一个新的节点1，直接插入则会打破平衡，此时不平衡点出现在6，则需要进行左旋调整

（1）节点的左孩子替代此节点位置 （2）左孩子的右子树变为该节点的左子树 （3）节点本身变为左孩子的右子树

左右旋转（RL）

插入的元素在不平衡的节点的右侧的左侧
插入5

先对7左旋

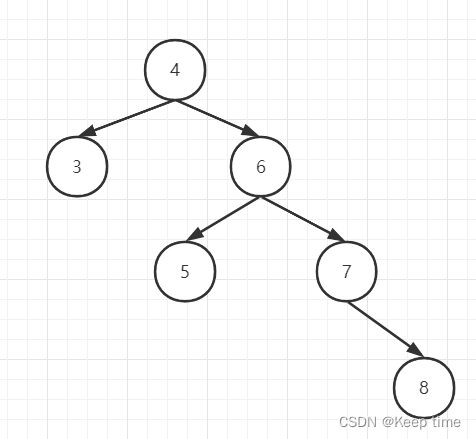
对4右旋

右左旋转（LR）

插入的元素在不平衡的节点的左侧的右侧
插入6

先对4进行右旋

再对7进行左旋

代码实现

public class AVLTreeMap<K extends Comparable<K>, V> implements Map<K, V> {
    private Node node;

    private class Node {
        public K key;
        public V value;
        public Node left;
        public Node right;
        public int height;

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            this.height = 1;
        }
    }
    private Node root;
    private int size;

    public AVLTreeMap() {
        this.root = null;
        this.size = 0;
    }

    /**
     * 右旋转
     * @param node 需要旋转的节点
     * @return 旋转后节点
     */
    private Node rightRotate(Node node) {
        //（1）节点的左孩子替代此节点位置
        Node leftChild = node.left;
        // （2）左孩子的右子树变为该节点的左子树
        Node lCR = leftChild.right;
        node.left = lCR;
        // （3）节点本身变为左孩子的右子树
        leftChild.right = node;
        // 对高度重新赋值
        leftChild.height = Math.max(getHeight(leftChild.left), getHeight(leftChild.right)) + 1;
        node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
        return leftChild;
    }

    /**
     * 左旋转
     * @param node 需要旋转的节点
     * @return 旋转后节点
     */
    private Node leftRotate(Node node) {
        // （1）节点的右孩子替代此节点位置
        Node rightChild = node.right;
        // （2）右孩子的左子树变为该节点的右子树
        Node rCL = rightChild.left;
        node.right = rCL;
        // （3）节点本身变为右孩子的左子树
        rightChild.left = node;
        rightChild.height = Math.max(getHeight(rightChild.left), getHeight(rightChild.right)) + 1;
        node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
        return rightChild;
    }

    /**
     * 获取高度
     * @param node 节点
     * @return 节点高度
     */
    private int getHeight(Node node) {
        if (node == null) {
            return 0;
        }
        return node.height;
    }

    @Override
    public void put(K key, V value) {
        root = put(root, key, value);
    }

    private Node put(Node node, K key, V value) {
        if (node == null) {
            size++;
            return new Node(key, value);
        }
        // 二分查找key是否存在
        if (key.compareTo(node.key) < 0) {
            node.left = put(node.left, key, value);
        } else if (key.compareTo(node.key) > 0) {
            node.right = put(node.right, key, value);
        } else {
            // 存在key 修改value
            node.value = value;
        }
        // 更新node高度
        node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
        // 判断node是否平衡
        // 获取左右高度差值
        int balanceFactory = getBalanceFactory(node);
        // 判断需要旋转的情况
        if (balanceFactory > 1 && getBalanceFactory(node.left) >= 0) {
            // 左左
            return rightRotate(node);
        }
        if (balanceFactory < -1 && getBalanceFactory(node.right) < 0) {
            // 右右·
            return leftRotate(node);
        }
        if (balanceFactory > 1 && getBalanceFactory(node.left) < 0) {
            // 左右
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
        if (balanceFactory < -1 && getBalanceFactory(node.right) >= 0) {
            // 右左
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

    /**
     * 判断左右差值
     * @param node 节点
     * @return 节点差值
     */
    private int getBalanceFactory(Node node) {
        if (node == null) {
            return 0;
        }
        return getHeight(node.left) - getHeight(node.right);
    }

    @Override
    public V remove(K key) {
        Node delNode = getNode(root, key);
        if (delNode != null) {
            root = remove(root, key);
            return delNode.value;
        }
        return null;
    }

    private Node remove(Node node, K key) {
        if (node == null) {
            return null;
        }
        Node retNode = null;
        if (key.compareTo(node.key) < 0) {
            node.left = remove(node.left, key);
            retNode = node;
        } else if (key.compareTo(node.key) > 0) {
            node.right = remove(node.right, key);
            retNode = node;
        } else {
            // 找到了
            if (node.left == null) {
                Node rightNode = node.right;
                node.right = null;
                size--;
                retNode = rightNode;
            } else if (node.right == null) {
                Node leftNode = node.left;
                node.left = null;
                size--;
                retNode = leftNode;
            } else {
                Node successor = minimum(node.right);
                successor.right = remove(node.right, successor.key);
                successor.left = node.left;
                node.left = null;
                node.right = null;
                retNode = successor;
            }
        }
        if (retNode == null) {
            return retNode;
        }
        retNode.height = Math.max(getHeight(retNode.left), getHeight(retNode.right)) + 1;
        int balanceFactory = getBalanceFactory(retNode);
        if (balanceFactory > 1 && getBalanceFactory(retNode.left) >= 0) {
            return rightRotate(retNode);
        }
        if (balanceFactory < -1 && getBalanceFactory(retNode.right) < 0) {
            return leftRotate(retNode);
        }
        if (balanceFactory > 1 && getBalanceFactory(retNode.left) < 0) {
            retNode.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }
        if (balanceFactory < -1 && getBalanceFactory(retNode.right) >= 0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }
        return retNode;
    }

    /**
     * 获取节点下最小元素
     * @param node 节点
     * @return 节点下最小节点
     */
    private Node minimum(Node node) {
        if (node.left == null) {
            return node;
        }
        return minimum(node.left);
    }

    private Node getNode(Node node, K key) {
        if (node == null) {
            return null;
        }
        if (key.compareTo(node.key) < 0) {
            return getNode(node.left, key);
        } else if (key.compareTo(node.key) > 0) {
            return getNode(node.right, key);
        } else {
            return node;
        }
    }

    @Override
    public boolean contains(K key) {
        return getNode(root, key) != null;
    }

    @Override
    public V get(K key) {
        Node node = getNode(root, key);
        return node == null ? null : node.value;
    }

    @Override
    public void set(K key, V value) {
        Node node = getNode(root, key);
        if (node == null) {
            throw new IllegalArgumentException("entry is not exist");
        }
        node.value = value;
    }

    @Override
    public int size() {
        return size;
    }

    @Override
    public boolean isEmpty() {
        return size == 0 && root == null;
    }

    @Override
    public Set<K> keySet() {
        TreeSet<K> set = new TreeSet<>();
        inOrderKeySet(root, set);
        return set;
    }

    private void inOrderKeySet(Node node, TreeSet<K> set) {
        if (node == null) {
            return;
        }
        inOrderKeySet(node.left, set);
        set.add(node.key);
        inOrderKeySet(node.right, set);
    }

    @Override
    public List<V> values() {
        LinkedList<V> list = new LinkedList<>();
        inOrderValues(root, list);
        return list;
    }

    private void inOrderValues(Node node, LinkedList<V> list) {
        if (node == null) {
            return;
        }
        inOrderValues(node.left, list);
        list.add(node.value);
        inOrderValues(node.right, list);
    }

    @Override
    public Set<Entry<K, V>> entrySet() {
        TreeSet<Entry<K, V>> set = new TreeSet<>();
        inOrderEntrySet(root, set);
        return set;
    }

    private void inOrderEntrySet(Node node, TreeSet<Entry<K, V>> set) {
        if (node == null) {
            return;
        }
        inOrderEntrySet(node.left, set);
        set.add(new BSTEntry<>(node.key, node.value));
        inOrderEntrySet(node.right, set);
    }
    
    private class BSTEntry<K extends Comparable<K>, V> implements Entry<K, V> {
        private K key;
        private V value;

        public BSTEntry(K key, V value) {
            this.key = key;
            this.value = value;
        }

        @Override
        public K getK() {
            return key;
        }

        @Override
        public V getV() {
            return value;
        }

        @Override
        public int compareTo(Entry<K, V> o) {
            return key.compareTo(o.getK());
        }
    }
}