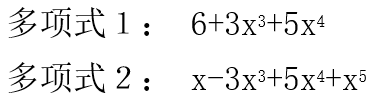数据结构 C++实现一元多项式运算(链式存储)
文章目录
- 一、实验目的
- 二、实验内容
- 三、代码内容
-
- 1、多项式创建
- 2、输出函数
- 3、多项式加减法
- 4、冒泡排序
- 5、多项式乘法
- 6、总代码
- 四、运行结果
- 五、总结
一、实验目的
1、 了解线性表的特性,以及它在实际问题中的应用。
2、掌握线性表的链式存储的实现方法以及它的基本操作,学会运用单链表来解决问题。
二、实验内容
题目:用带头节点的单链表存储一元多项式的每一项,实现求一元多项式的加法、减法和乘法。具体要求为:用五个函数分别实现一元多项式的创建、输出、加法、减法和乘法;然后在主函数中调用这些函数实现这些功能的展示,以菜单的形式呈现。
三、代码内容
1、多项式创建
可以乱序输入多项式,在创建时自动会升序排序
void creatlist(polynomial &p) {
//输入n项的系数和指数,建立表示多项式的有序链表p
p = new PNode; //为链表P1申请一个空间;
int n;
cout << "请输入多项式项数:";
cin >> n;
p->next = NULL; //建立一个带头节点的单链表
polynomial t,q; //用于标记位置
for (int i = 1; i <= n; i++) {//依次输入n个非0项,并将他们排序
polynomial s = new PNode; //生成一个新节点,用于存储输入的系数和指数
cout << "请分别输入系数和指数: " ;
cin >> s->coef >> s->expn; //输入系数和指数
t = p; //t用于保存q的前驱,初值为头节点,为了让p只表示头节点
q = p->next; //q初始化,指向首元节点
while (q && q->expn < s->expn) {//从头到尾开始比较指数找到第一个大于输入指数的项*q
t = q;
q = q->next; //q指向下一个节点
} //while
s->next = q; //将输入项s插入到q和其他前驱节点pre之间
t->next = s;
} //for
}
2、输出函数
最后一项的输出带有“+”而我用’\b’并没有消除加号,我只好先遍历出多项式系数再单独输出最后一项
void printout(polynomial p) {
int n = 0;
polynomial t = p;
while (t=t->next) {
n++; //多项式项数
} //while
p = p->next;
for (int i = 1; i < n; i++) {
if (p->coef != 0 && p->expn == 0) //判断是否为常数项
cout << p->coef << "+";
else if (p->coef < 0) {
cout << "\b";
cout << p->coef << "x^" << p->expn << "+";
}
else
cout << p->coef << "x^" << p->expn << "+";
p = p->next;
}
//单独输出最后一项
if (p->coef < 0) {
cout << "\b";
cout << p->coef << "x^" << p->expn;
}
else
cout << p->coef << "x^" << p->expn;
}
3、多项式加减法
加法和减法的实现没有太大变化
这里我为了节约空间没有创建储存空间,把结果保存到的p1的空间中
这也导致了后续想要进行加减法运算需要重建输入多项式
//多项式加法
void add_polynomial(polynomial p1,polynomial p2) {
//多项式加法:p1=p1+p2,利用两个多项式的节点构成“和多项式”
polynomial t = p1; //t指向p1的头节点
polynomial flag = t; //用来标记p1的头节点
p1 = p1->next;
p2 = p2->next; //p1,p2分别指向首元节点
while (p1 && p2) { //p1,p2均非空时运行
if (p1->expn == p2->expn) { //指数相等时
p1->coef += p2->coef; //系数相加,存的p1里
if (p1->coef) { //coef不等于0时
t->next = p1; //将修改后的p1当前节点链在t之后
t = p1; //t指向p1
p1 = p1->next; //p1指向下一项
polynomial r = p2; //临时存储p2节点
p2 = p2->next; //p2后移
delete r; //删除原p2节点
}
else { //系数和为0
polynomial r = p1; //临时存储p1节点
p1 = p1->next; //p1后移
delete r; //删除原p1节点
polynomial rr = p2; //临时存储p2节点
p2 = p2->next; //p2后移
delete rr; //删除原p2节点
}
}
else if (p1->expn < p2->expn) { //p1指数小于p2指数
t->next = p1; //将修改后的p1当前节点链在t之后,
t = p1; //t指向p1
p1 = p1->next; //指向下一项
}
else { //p1的指数大于p2的指数
t->next = p2; //将修改后的p2当前节点链在t之后,
t = p2; //t指向p2
p2 = p2->next; //指向下一项
}
} //while
t->next = p1 ? p1 : p2; //插入非空多项式的剩余片段
cout << "相加的结果为:" << endl;
printout(flag); //输出结果
delete p2; //释放p2空间
}
//多项式减法
void subtruct_polynomial(polynomial p1,polynomial p2) {
//多项式减法:p1=p1-p2,利用两个多项式的节点构成“和多项式”
polynomial t = p1; //t指向p1的头节点
polynomial flag = t; //用来标记p1的头节点
p1 = p1->next;
p2 = p2->next; //p1,p2分别指向首元节点
while (p1 && p2) { //p1,p2均非空时运行
if (p1->expn == p2->expn) { //指数相等时
p1->coef -= p2->coef; //系数相减,存的p1里
if (p1->coef) { //coef不等于0时
t->next = p1; //将修改后的p1当前节点链在t之后,
t = p1; //t指向p1
p1 = p1->next; //p1指向下一项
polynomial r = p2; //临时存储p2节点
p2 = p2->next; //p2后移
delete r; //删除原p2节点
}
else { //系数差为0
polynomial r = p1; //临时存储p1节点
p1 = p1->next; //p1后移
delete r; //删除原p1节点
polynomial rr = p2; //临时存储p2节点
p2 = p2->next; //p2后移
delete rr; //删除原p2节点
}
}
else if (p1->expn < p2->expn) { //p1指数小于p2指数
t->next = p1; //将修改后的p1当前节点链在t之后,
t = p1; //t指向p1
p1 = p1->next; //指向下一项
}
else { //p1的指数大于p2的指数
p2->coef *= -1; //系数要乘-1变成相反数
t->next = p2; //将修改后的p2当前节点链在t之后,
t = p2; //t指向p2
p2 = p2->next; //指向下一项
}
} //while
if (p1)
t->next = p1; //插入剩余片段
if (p2)
while (p2) {
p2->coef *= -1; //系数要乘-1变成相反数
t->next = p2; //将修改后的p2当前节点链在t之后,
t = p2; //t指向p2
p2 = p2->next; //指向下一项
}
cout << "相减的结果为:" << endl;
printout(flag); //输出结果
delete p2; //释放p2空间
}
4、冒泡排序
为了后续乘法运算做铺垫
//排序函数
void sort(polynomial p,polynomial head) {
p = head;
polynomial t1 = p->next;
polynomial t2 = p->next;
polynomial t3 = NULL;
float ct;
int et;
//冒泡排序
while (t2!=t3) { //t1非空
while (t1->next!=t3) {
if ((t1->expn) > (t1->next->expn)) {
ct = t1->coef;
t1->coef = t1->next->coef;
t1->next->coef = ct;
et = t1->expn;
t1->expn=t1->next->expn;
t1->next->expn = et;
}//if
t1 = t1->next;
} //while
t3 = t1;
t1 = p->next; //t1重置
}//while
}
5、多项式乘法
乘法运算:先相乘,然后再排好序,最后再合并同类项
void multiply_polynomial(polynomial& p1, polynomial& p2) {
//先相乘,再排序,后合并
polynomial head2 = p2; //标记p2头结点
polynomial head = new PNode;
polynomial flag;
flag = head;
//先相乘
p1 = p1->next;
p2 = p2->next;
while (p1) {//为NULL时退出循环
while (p2) {//为NULL时退出循环
polynomial t = new PNode;
t->coef = p1->coef * p2->coef; //系数相加,存到t中
t->expn = p1->expn + p2->expn; //指数相加
flag->next = t;
t->next = NULL;
flag = t;
p2 = p2->next;
}
p1 = p1->next;
p2 = head2->next; //重置p2
} //while
//再排序
sort(flag, head);
//合并
for (polynomial q = head->next; q && q->next;) {
if (q->expn == q->next->expn) {
q->coef += q->next->coef; //系数相加
q->next = q->next->next; //后一位插入
}
else q = q->next;
} //for
cout << "相乘的结果为:" << endl;
printout(head); //输出结果
}
6、总代码
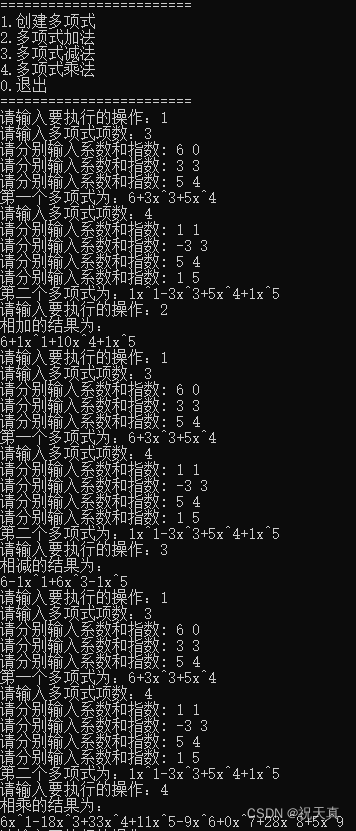
#include四、运行结果
五、总结
这个程序还有很多不足之处,输出多项式时最后一项的“+”为什么不能用‘\b’删除,多项式的加减乘没有使用储存空间导致每次运算都需要重新输入等等,如果有人知道为什么输出多项式时最后一项的“+”为什么不能用‘\b’删除,希望能教教我。