第一章 工程师数学算法库之线性代数矩阵运算库Eigen的使用

现在有很多的科学计算软件，matlab，开源库。这些都是国外的，中国人能不能有自己的数学算法库呢？
工程师需要的是一个可以移植的算法库，而不太想了解库背后纷繁复杂的理论。我之后会开一个专栏，学习数学算法的同时分享这些算法，尽量让工程师拥有一个可以拿来就移植的算法包。

> 2020/01/28 我可能太乐观了，重新实现一遍数学算法是不是太难了，意义也不大呢？对于工程师，最想要的是能直接拿来就能用的库，移植方便，算法效率高，最好不收费。

---

工程师数学算法库系列

第一章 工程师数学算法库之线性代数矩阵运算库Eigen的使用

---

目录

一、移植Eigen的方法

二、Eigen具有的具体功能

三、Eigen的详细介绍（包含对运行效率的分析）

3.1 矩阵数据类型

3.2 定义大矩阵的方法（行列大小大于16）

3.3 矩阵初始化方式

3.4 矩阵运算

3.5 矩阵分解（还需验证）

3.6 线性方程求解

3.7 欧拉角和四元数转化

四、使用的技巧和注意事项

五、致谢

---

前言：我所使用的Eigen版本是Eigen3.3.5，因此后面所有的代码示例和解释都是基于此的。时间：2020/01/28

一、移植Eigen的方法

我也是从这个csdn地址下载的，代码包下载地址：https://download.csdn.net/download/qq21497936/10800291

亲测可用！！！

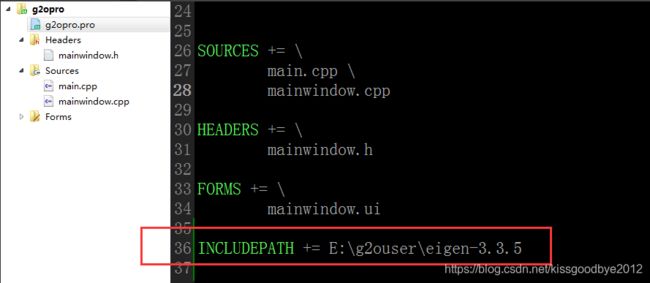
Eigen的移植非常简单，只需一步。随便将Eigen放置在任何位置，当然最好别有中文路径（我也没试过，最好别吧，外国的中文适配不是那么好）。移植方法：使用时将Eigen的头文件路径包含就行。

例子，QT里如下，其实就是让IDE可以找到你的头文件就行，这里真的感谢开源Eigen的作者们，真的方便！：

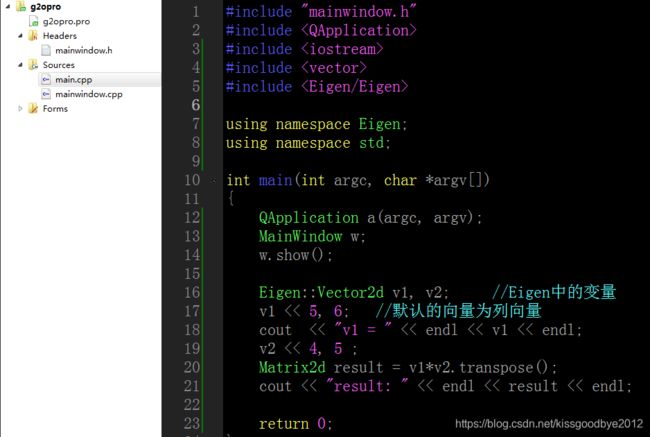
给大家一段验证是否移植好的代码，这个是转自博客：https://www.cnblogs.com/tornadomeet/archive/2012/12/11/2813842.html：

#include 
#include 

using namespace Eigen;
using namespace std;

int main(int argc, char *argv[])
{
   Eigen::Vector2d v1, v2;     //Eigen中的变量
    v1 << 5, 6;   //默认的向量为列向量
    cout  << "v1 = " << endl << v1 << endl;
    v2 << 4, 5 ;
    Matrix2d result = v1*v2.transpose();
    cout << "result: " << endl << result << endl;

    return 0;
}

二、Eigen具有的具体功能

Eigen的官网：http://eigen.tuxfamily.org/dox/group__TutorialMatrixClass.html

但官网好像转移到gitlab了，具体见官网上的公告。

 

讨论：

1.稠密矩阵是每个元素都存储的，而稀疏矩阵是将非零元素存储成一个表；

2.固定矩阵对于小矩阵非常适用（矩阵大小最大4X4，有时到16X16），在编译的时候就已知矩阵大小；而对于大矩阵，一般适用动态矩阵，即使编译时就知道矩阵大小；这里涉及内存大小的分配，对于动态矩阵，在堆中动态分配内存大小；

 

三、Eigen的详细介绍（包含对运行效率的分析）

前言：我的机器配置

用了多年的acer机(2012年买的)，配置如下：

对于效率的计算，多次运算取最大时间为测试值。

3.1 矩阵数据类型

矩阵类如下，是一个模板类：

template  class Eigen::Matrix< _Scalar, _Rows, _Cols, _Options, _MaxRows, _MaxCols >

注意：

1.这个类不仅可以用于矩阵，也可用于行向量和列向量；

2.这个矩阵类也同时适合固定大小的矩阵和可变大小的矩阵；

参数说明，前三个参数是必须有的：

参数1，_Scalar：矩阵元素的数据类型，包括float, double, int or std::complex；

参数2，_Rows： 矩阵的行数，可以为具体值，也可以动态指定；

参数3，_Cols：   矩阵的列数，可以为具体值，也可以动态指定；

预定义类型，就是常用的提前定义好的矩阵类，方便使用。

更多的预定义类型见：http://eigen.tuxfamily.org/dox/group__matrixtypedefs.html：

• Matrix2d 是一个 2x2 doubles类型方阵 (Matrix)
• Vector4f 是一个大小为4的floats类型向量 (Matrix)
• RowVector3i 是一个大小为3的int类型行向量 (Matrix)

• MatrixXf 是一个动态大小的floats类型矩阵(Matrix)
• VectorXf 是一个动态大小的floats类型向量(Matrix)

• Matrix2Xf 是一个部分固定大小的floats类型矩阵 (Matrix)
• MatrixX3d 是一个部分固定大小的double类型矩阵 (Matrix)

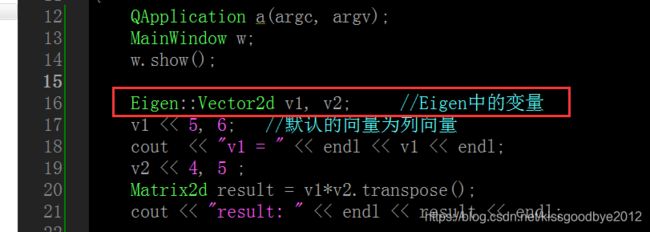
注意：这些预定义类的命名空间为Eigen，使用的时候如下图所示。如果加了using namespace Eigen;也可以不加前面的Eigen：。

3.2 定义大矩阵的方法（行列大小大于16）

根据前面3.1的介绍，去定义一个m x n的矩阵其实是一件非常容易的事。但我们定义的矩阵是要进行运算的，直接定义一个大矩阵非常容易造成内存超限（栈溢出），这个时候可以通过定义动态矩阵的方法，避免这个问题。动态矩阵在赋值或者运算的时候，自动产生对应的维数大小。

注意：动态矩阵在赋值后，运算过程中矩阵大小也是可以变化的。也就是说，一旦定义为动态矩阵，它的维度就是随时可变的。

例如，先前我们创建的如下面形式的矩阵：

Eigen::Matrix matrix_NN;

改成动态矩阵的形式：

Eigen::Matrix matrix_NN;
matrix_NN = Eigen::MatrixXd::Random(500, 500);

//或者更加一般的赋值方法如下
Matrix a;
double t[] = {1,2,3,4};
a= Map >(t);//RowMajor代表行优先

3.3 矩阵初始化方式

（1）随机值初始化矩阵

Matrix p=Matrix::Random();//一般的矩阵随机初始化
matrix_NN = Eigen::MatrixXd::Random(500, 500);//动态矩阵随机初始化

（2）单位矩阵初始化矩阵

Matrix p=Matrix::Identity(5);//定义并初始化矩阵
std::cout <<  matrix_NN << std::endl;//显示矩阵

（3）零矩阵初始化矩阵

Matrix p=Matrix::Zero();//定义并初始化矩阵
std::cout <<  p << std::endl;//显示矩阵
matrix_NN = Eigen::MatrixXd::Zero(500, 500);

（4）用指定值初始化矩阵

Matrix p=Matrix::Constant(5);//定义并初始化矩阵
std::cout <<  p << std::endl;//显示矩阵

（5） 矩阵赋值

方法1：逗号初始化

Eigen提供了逗号操作符允许我们方便地为矩阵/向量/数组中的元素赋值。按从左到右，从上到下的顺序列出所有元素，并用逗号进行分隔。需要注意的是，对象的尺寸需要事先指定，而且所列出的元素数目要和操作对象的尺寸大小一致。

注意：

1. 这样赋值一定要完成赋值充分，不能留几个元素不赋值，否则计算会报错：初始化未完成，结果是末尾会补零进行计算。

    Matrix2d a;
    a << 1, 2, 3, 4;
    MatrixXd b(2,2);
    b << 2, 3, 1, 4;

2. 不仅可以用数值进行赋值，还可以通过多个向量进行赋值，如下：看最后一个joined矩阵，是用两个向量来赋值的

RowVectorXd vec1(3);
vec1 << 1, 2, 3;
std::cout << "vec1 = " << vec1 << std::endl;
RowVectorXd vec2(4);
vec2 << 1, 4, 9, 16;
std::cout << "vec2 = " << vec2 << std::endl;
RowVectorXd joined(7);
joined << vec1, vec2;
std::cout << "joined = " << joined << std::endl;

3. 还可以通过矩阵块来进行赋值，就像拼图一样，哈哈

MatrixXf matA(2, 2);
matA << 1, 2, 3, 4;
MatrixXf matB(4, 4);
matB << matA, matA/10, matA/10, matA;
std::cout << matB << std::endl;

结果如下：

1     2   0.1 0.2
3     4   0.3 0.4
0.1 0.2   1     2
0.3 0.4   3     4

4.还可以通过块表达式进行赋值（这个还不太懂）（还需验证）

Matrix3f m;
m.row(0) << 1, 2, 3;
m.block(1,0,2,2) << 4, 5, 7, 8;
m.col(2).tail(2) << 6, 9;                   
std::cout << m;

结果如下：

1 2 3
4 5 6
7 8 9

3.4 矩阵运算

（1）矩阵加减法

直接加和减就行，但得注意矩阵行列数得相同，否则程序会报错。报错也会有结果输出，这个结果是按照最小行列数的矩阵来计算的，不足的会补零。

  Matrix2d a;
  a << 1, 2,
       3, 4;
  MatrixXd b(2,2);
  b << 2, 3,
       1, 4;
  std::cout << "a + b =\n" << a + b << std::endl;
  std::cout << "a - b =\n" << a - b << std::endl;

加法的计算效率结果如下（减法的没测，2000那组结果差不多），单位ms，注意200 x 200的时候程序已经提示矩阵过大，后来改用动态矩阵了：

	ACER	小新潮7000	华硕电脑
2 X 2	0
20 X 20	0
200 X 200	3
2000 X 2000	128

（2）矩阵乘法

    Matrix a;
    double t[] = {1,2,3,4};
    a= Map >(t);

    Matrix b;
    double tt[] = {2,3,4,5};
    b= Map >(tt);

    std::cout << "a * b =\n" << a * b << std::endl;

乘法的计算效率结果如下，单位ms，采用动态矩阵：

	ACER	小新潮7000	华硕电脑
2 X 2	0
20 X 20	1
200 X 200	227
2000 X 2000	超长时间

（3）求矩阵行列式

double p=a.determinant();

（4）求逆矩阵，伴随矩阵，矩阵转置（还需验证）

    std::cout << "p=\n" << a.transpose() << std::endl;//转置矩阵
    std::cout << "p=\n" << a.adjoint() << std::endl;//伴随矩阵
    std::cout << "p=\n" << a.inverse() << std::endl;//逆矩阵

（5）求矩阵特征值（还需验证）

    MatrixK= MatrixXd::Random(4,4);
    EigenSolver> es(K);
    MatrixXcd evecs = es.eigenvectors();//获取矩阵特征向量4*4，这里定义的MatrixXcd必须有c，表示获得的是complex复数矩阵
    MatrixXcd evals = es.eigenvalues();//获取矩阵特征值 4*1
    MatrixXd evalsReal;//注意这里定义的MatrixXd里没有c
    evalsReal=evals.real();//获取特征值实数部分
    MatrixXf::Index evalsMax;
    evalsReal.rowwise().sum().maxCoeff(&evalsMax);//得到最大特征值的位置
    Vector4d q;
    q << evecs.real()(0, evalsMax), evecs.real()(1, evalsMax), evecs.real()(2, evalsMax), evecs.real()(3, evalsMax);//得到对应特征向量

3.5 矩阵分解（还需验证）

分解一：Cholesky分解

x3 = (A.transpose()*A).llt().solve(A.transpose()*b);  //方法3：choleskey分解。

分解二：LU三角分解

 

分解三：QR分解

 

分解四：奇异值分解

 

分解五：LDLT分解

#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace Eigen;

#define MATRIX_SIZE 100

int main()
{
//方程组形式Ax = b；（假定A是方阵）
 Matrix A;
 A = MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);

Matrix b;
b = MatrixXd::Random(MATRIX_SIZE,1);

Matrix x1;
Matrix x2;
Matrix x3;
Matrix x4;

clock_t  time_stt = clock();
x1 = A.inverse()*b;       //方式1：直接求逆求解x = A的逆 * b
cout<<"x1 time is:"<<1000*(clock()-time_stt)/(double)CLOCKS_PER_SEC<<"ms"<

3.6 线性方程求解

    //计算Ax=b;
    Eigen::Matrix3d A;
    A<<1,1,1,1,2,3,3,2,3;
    Eigen::Matrix b;
    b<<3,6,8;
    cout<<"行列式为："<3.7 欧拉角和四元数转化 
  
（1）欧拉角转四元数
 
  
先旋转x轴，然后旋转y轴，最后旋转z轴，对应的旋转角分别为rx, ry, rz，即ea[2] ea[1] ea[0]
 
  
q = Eigen::AngleAxisd(ea[0], ::Eigen::Vector3d::UnitZ()) *
Eigen::AngleAxisd(ea[1], ::Eigen::Vector3d::UnitY()) *
Eigen::AngleAxisd(ea[2], ::Eigen::Vector3d::UnitX());
 
  
（2）四元数转欧拉角
 
  
按照先旋转ｘ轴(0)，然后y轴(1)，最后z轴得到的角度，并不是传统意义上，zyx旋转的欧拉角。
 
  
得到的ea向量，分别对应的是rz, ry, rx旋转角度，注意和下文的顺序对应
 
  
另外这里得到的角度，归一化的范围有些问题，代码中的说明是 
 
  
The returned angles are in the ranges [0:pi] x [-pi:pi] x [-pi:pi].
 所以，这里的rz角范围可能有问题，需要注意
 
  
Eigen::Quaterniond q(w, x, y, z);
Eigen::Matrix3d rx = q.toRotationMatrix();
Eigen::Vector3d ea = rx.eulerAngles(2,1,0);
 
  
四、使用的技巧和注意事项
 
  
 
 
  
五、致谢
 
  
感谢下面这些博客提供的参考
 
  
矩阵初始化相关：https://blog.csdn.net/wangxiao7474/article/details/103520425
 
  
动态矩阵赋值相关：https://blog.csdn.net/sinat_28751869/article/details/79425491
 
  
矩阵的特征值相关：https://blog.csdn.net/wcsgzc/article/details/53946345
 
  
四元数和欧拉角相关：
 
  
https://blog.csdn.net/heroacool/article/details/103288585
 
  
https://blog.csdn.net/DaqianC/article/details/81474338