C语言实现实数和复数矩阵及其各种运算(二)
一、前言
- 由于实数矩阵的运算较简单,因此在本章中,我只给出复数矩阵的相关运算,一般的实数矩阵,类似炮制即可;
- 复数矩阵的加/减/乘运算涉及到其复数元胞(cell)的相加减运算,由于complex.h头文件中只给出了复数乘法运算,故而复数的加减运算函数需要自己定义功能。
二、矩阵加/减法运算
即复数矩阵与复数矩阵之间的加/减法运算:
/* Complex Matrix Add: matrixC = matrixA + matrixB */
void AddMatrix(const Matrix* matrix_A, const Matrix* matrix_B, Matrix* matrix_C)
{
// Size Incompatability
if (matrix_A->row == matrix_B->row || matrix_A->column == matrix_B->column)
{
puts("ERROE: An incompatable matrix!\n");
return;
}
// Validity of Known Matrice
else if (IsNullComplexMatrix(matrix_A) || IsNullComplexMatrix(matrix_B))
{
puts("ERROE: An invalid matrix!\n");
return;
}
else
{
ComplexType tempCell_C;
int indexC;
for (int row_i = 0; row_i < matrix_C->row; row_i++)
{
for (int column_j = 0; column_j < matrix_C->column; column_j++)
{
tempCell_C = AddComplex(matrix_A->arrayComplex[row_i * matrix_A->column + column_j],
matrix_B->arrayComplex[row_i * matrix_B->column + column_j]);
indexC = row_i * matrix_C->column + column_j;
matrix_C->arrayComplex[indexC] = tempCell_C;
// matrix_C->arrayComplex[i * matrix_C->row + j]._Val[0] = \
// creal(matrix_A->arrayComplex[i * matrix_A->row + j]) + creal(matrix_B->arrayComplex[i * matrix_A->row + j]);
// matrix_C->arrayComplex[i * matrix_C->row + j]._Val[1] = \
// cimag(matrix_A->arrayComplex[i * matrix_A->row + j]) + cimag(matrix_B->arrayComplex[i * matrix_A->row + j]);
}
}
}
}
说明:
加减法运算简单,笔者这里就不给出测试了!!!
三、矩阵乘法运算
矩阵乘法运算用到非常多!!!
1.复数加法运算
即复数与复数之间对应实/虚部相加:
/* Add Complex: Complex_C = Complex_A + Complex_B */
ComplexType AddComplex(const ComplexType Complex_A, const ComplexType Complex_B)
{
ComplexType Complex_C;
Complex_C._Val[0] = creal(Complex_A) + creal(Complex_B);
Complex_C._Val[1] = cimag(Complex_A) + cimag(Complex_B);
return Complex_C;
}
说明:
后续的矩阵乘法运算用到加法函数,故而不单独测试。
2.复数减法运算
即复数与复数之间对应实/虚部相减:
/* Subvision Complex: Complex_C = Complex_A - Complex_B */
ComplexType SubComplex(const ComplexType Complex_A, const ComplexType Complex_B)
{
ComplexType Complex_C; // Change Pointer to a Variable
Complex_C._Val[0] = creal(Complex_A) - creal(Complex_B);
Complex_C._Val[1] = cimag(Complex_A) - cimag(Complex_B);
return Complex_C;
}
说明:
后续的矩阵乘法运算用到减法函数,故而不单独测试。
3.矩阵数乘运算
数乘运算,也就是复数矩阵与实数和复数矩阵与复数的乘法运算:
/* Point Multiple: Complex matrixB = Complex matrixA .* Complex_c */
void MatrixPointMulComplex(const Matrix* matrixA, ComplexType c, Matrix* matrixB)
{
if (IsNullComplexMatrix(matrixA))
{
puts("ERROE: An invalid matrix!\n");
return;
}
else
{
int row_i, column_j;
for (row_i = 0; row_i < matrixB->row; ++row_i)
for (column_j = 0; column_j < matrixB->column; ++column_j)
{
matrixB->arrayComplex[row_i * matrixB->column + column_j] =
_Cmulcc(matrixA->arrayComplex[row_i * matrixA->column + column_j], c);
}
}
}
/* Point Multiple: Complex matrixB = Complex matrixA .* Double_c */
void MatrixPointMulDouble(const Matrix* matrixA, DoubleType c, Matrix* matrixB)
{
if (IsNullComplexMatrix(matrixA))
{
puts("ERROE: An invalid matrix!\n");
return;
}
int row_i, column_j;
for (row_i = 0; row_i < matrixB->row; ++row_i)
for (column_j = 0; column_j < matrixB->column; ++column_j)
{
matrixB->arrayComplex[row_i * matrixB->column + column_j] = \
_Cmulcr(matrixA->arrayComplex[row_i * matrixA->column + column_j], c);
}
}
说明:
(1) 这里笔者贴上复数矩阵与复数和复数矩阵与实数的点乘运算两个函数;
(2) 核心就是调用复数与复数乘法函数_Cmulcc()和复数与实数乘法函数_Cmulcr(),其函数原型:
_ACRTIMP _Dcomplex __cdecl _Cmulcc(_In_ _Dcomplex _X, _In_ _Dcomplex _Y);
_ACRTIMP _Dcomplex __cdecl _Cmulcr(_In_ _Dcomplex _X, _In_ double _Y);
(3) 同样在主程序之前都加上一个if判断语句,用于保证传入的实参矩阵是有效,才有计算的意义;
(4) 结合前面的函数,这里我给出测试复数矩阵与数乘的demo,顺便把第一章中的几个函数也测试了:
#include测试结果我直接通过截图的形式给出,VS C(上)和matlab(下):
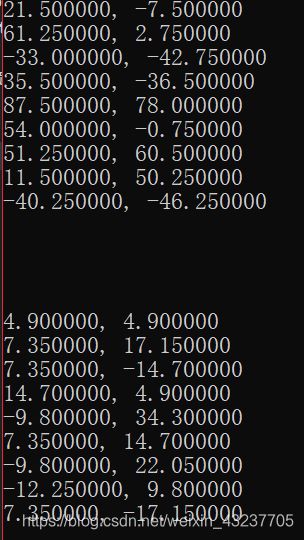


4.复数矩阵乘法运算
矩阵乘法运算,即复数矩阵与复数矩阵的运算:
/*
Complex Matrix Multiple: matrixC = matrixA * matrixB
*/
void MatrixMulMatrix(const Matrix* matrixA, const Matrix* matrixB, Matrix* matrixC)
{
if (IsNullComplexMatrix(matrixA) || IsNullComplexMatrix(matrixB)) // Validity of Known Matrice
{
puts("ERROE: An invalid matrix!\n");
return;
}
else if (matrixA->column != matrixB->row) // Incompatability of Size
{
puts("ERROE: An incompatable matrix!\n");
return;
}
else
{
int row_i, column_j, ij;
int indexA, indexB, indexC;
ComplexType tempCell_C; // Save Temp Value of Cell of Matrix C
for (row_i = 0; row_i < matrixC->row; ++row_i)
{
for (column_j = 0; column_j < matrixC->column; ++column_j)
{
tempCell_C._Val[0] = 0;
tempCell_C._Val[1] = 0;
for (ij = 0; ij < matrixA->column; ++ij)
{
indexA = row_i * matrixA->column + ij;
indexB = ij * matrixB->column + column_j;
tempCell_C = AddComplex(tempCell_C, \
_Cmulcc(matrixA->arrayComplex[indexA], matrixB->arrayComplex[indexB]));
/* temp._Val[0] = creal(temp) + creal(_Cmulcc(matrixA->arrayComplex[indexA], matrixB->arrayComplex[indexB]));
temp._Val[1] = cimag(temp) + cimag(_Cmulcc(matrixA->arrayComplex[indexA], matrixB->arrayComplex[indexB]));
*/
}
indexC = row_i * matrixC->column + column_j;
matrixC->arrayComplex[indexC] = tempCell_C;
}
}
}
}
说明:
(1) 这里我加入了多个if-else语句来约束矩阵乘法运算的行列大小要求,保障运算安全;
(2) 中途注释掉的是我之前没有调用_Cmulcc()函数自行实现的复数乘法运算,读者可以忽略;
(3) 测试此函数:
#include测试结果我直接通过截图的形式给出,VS C(上)和matlab(下):
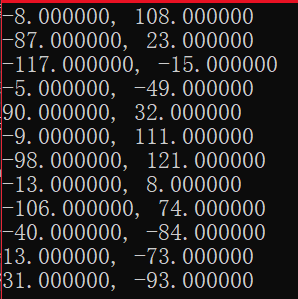

四、总结
矩阵之间的加/减/乘法运算较为简单,是矩阵运算最常见的功能,复数域和实数域的矩阵计算类似。下一章我将给出矩阵的转置、复制、代数余子式、逆的功能实现code,敬请期待…
传送门:(三)…