数据结构-堆的实现(详细图解+解说)

一.堆的基本概念

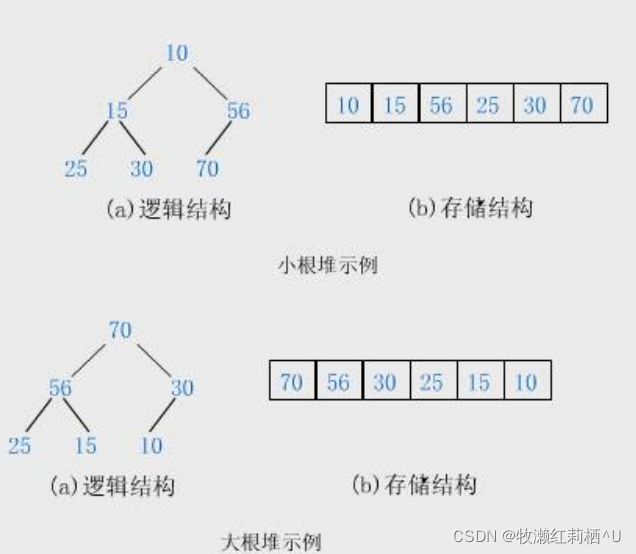
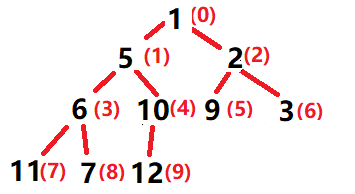
前文已经介绍了堆的基本概念,其在空间结构上是一个一维数组,而在逻辑结构上满足"父节点的值均不小于(不大于)子节点"。从逻辑结构上来看，堆是一颗完全二叉树。由父节点与子节点间的大小关系，又可划分为大堆和小堆，其中根节点为堆顶，而由于其结构，堆顶数据为堆中最大值(最小值)，其图示如下

二.堆的实现

1.堆的结构

堆的空间结构表现为一维数组，一般为了灵活使用，采用动态内存分配的方式进行创建，其结构定义类似于顺序表，此处不再赘述。

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

2.堆的实现

要实现堆，即需要在逻辑结构上满足堆的定义，并且需要我们实现以下功能，下面将逐个进行介绍，为了方便，以下实现以小堆为案例。

// 堆的构建
Heap* HeapCreate();
// 堆的销毁
void HeapDestroy(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
//向下调整算法
void AdjustDown(HPDataType* a, size_t size);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);

 1.堆的构建-HeapCreate函数

Heap* HeapCreate()
{
	Heap* tmp = (Heap*)malloc(sizeof(Heap));
	if (tmp == NULL)
	{
		printf("HeapCreate error\n");
		return NULL;
	}
	tmp->_a = NULL;
	tmp->_size = tmp->_capacity = 0;
	return tmp;
}

如上述代码，通过动态内存分配创建一个Heap*类型的变量，并对其指向的结构体变量_a,_size及_capacity进行初始化，返回此指针。

2.堆的数据插入-HeapPush函数

要了解堆的数据插入，就需要明白堆中父节点与子节点的关系。因为堆之所以为堆，便是由于其逻辑结构的特殊性。那么父节点和子节点之间有何关系呢？

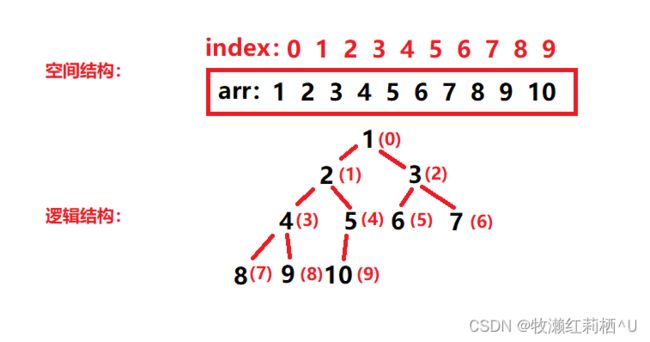
如图，将其下标为0处作为根节点，由于其为完全二叉树，子节点又分为左子节点和右子节点，因此从逻辑结构上我们可以看出，父节点(parent)和子节点(child1,child2)的下标满足如下关系:

由这两个公式，若我们已知父节点位置，便可推知子节点位置。

那么已知子节点，如何推知父节点呢？由上述两公式我们可知：

又由于我们发现，下标child1均为奇数，而下标child2均为偶数，利用C语言整除的特性，若已知child2，则公式也可以写为： 。因此对于任意一个子节点child(无论左右)，其父节点总满足：

有了如上分析，我们再来探讨如何在堆中插入数据:

在堆中未存放数据时，此时堆可视为空堆。现在要向其中插入数据，不同于顺序表的直接尾插，堆结构需要在插入数据后仍然保持结构成立-即父节点不大于子节点，那么如何才能从逻辑结构上维持堆结构呢？此时我们引进一个算法来解决这个问题。

---

---

-向上调整算法

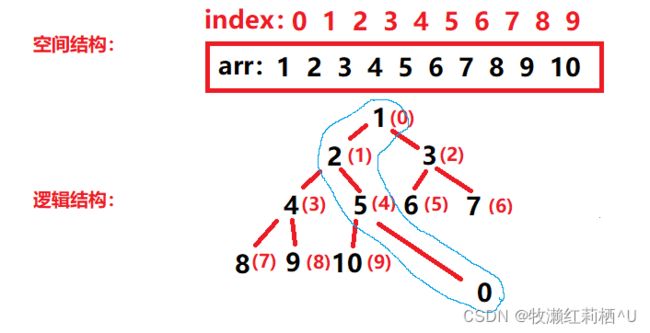
假设此时在上述堆中插入数据 0

 此时堆结构明显被破坏，因为不满足5不大于0。那么此时如何进行调整呢？

思路是:找到以子节点 0 为祖先结点的路径，在这条路径上，寻找其父节点 5 ，比较其大小，若不满足堆结构条件，则交换它们的值。然后将 5 作为子节点，继续向上查找父节点，比较其大小......直到满足堆结构条件或者寻找到根节点后，向上调整结束，此时堆结构得以维持。

对于此堆，1. 0 和 5进行交换，并将下标为4的位置为作为子节点继续向上调整，此时其数据为 0 。 2. 然后0 和 2 进行交换...... 3.最后 0 和 1 进行交换，子节点在下标为0处，此时查找到根节点，向上调整结束。

 调整后如图所示，满足堆结构。

下面进行代码实现:

//向上调整算法
void AdjustUp(HPDataType* a, size_t child)
{
	assert(a); //断言防止传入指针为空
	while (child != 0)
	{
		size_t parent = (child - 1) / 2;
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
		}
		else
		{
			break;
		}

		child = parent;
	}
}

和上文分析的逻辑一致，当child!=0时进入循环，计算父节点位置，然后进行比较。若此时a[child]>=a[parent]，则已经满足堆结构，break跳出循环。否则交换两者位置的值，并使child=parent，继续向上调整。若child=0，则说明已经向上调整至根节点，调整结束。

---

---

向上调整算法实现后，堆数据的插入便轻而易举，实质上便是'顺序表尾插' + '结构调整'，顺序表尾插我们都很熟悉，而结构调整由向上调整算法实现，易得代码如下:

void HeapPush(Heap* hp, HPDataType x)
{
	assert(hp);
	if (hp->_capacity <= hp->_size)
	{
		int newCapacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(hp->_a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc error\n");
			return;
		}
		hp->_a = tmp;
		hp->_capacity = newCapacity;
	}

	hp->_a[hp->_size] = x;
	AdjustUp(hp->_a, hp->_size); //向上调整算法
	hp->_size++;
}

上述代码中if语句内为判断空间是否足够，若不足则需先动态内存分配进行空间扩容，顺序表实现时已经多次提到，此处不再赘述。

2.堆的数据删除-HeapPop函数

要实现堆的删除，首先要明白何为堆的删除。堆的删除并不类似于顺序表的尾删，而是删除堆顶的数据，更类似于头删。前文提到过堆顶的数据是堆中的最大/最小值，这样删除也利于我们后面对堆结构的利用-如堆排序等。

然而我们能直接按照顺序表的头删方式对其进行删除吗?

 

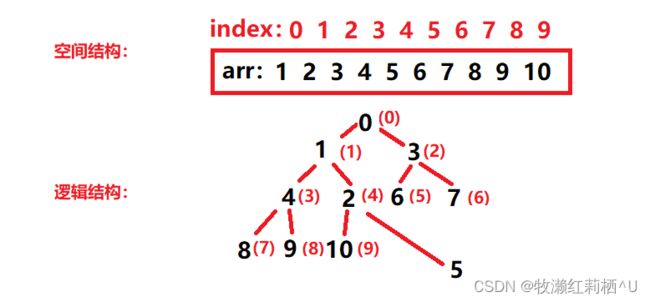
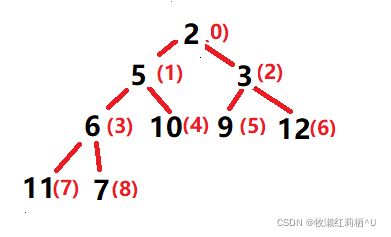
 如图为一个堆结构，加入按照顺序表的方式进行删除，即删除堆顶数据 1 ，空间结构上来看似乎很顺理成章，然而逻辑结构发生了何种改变呢?

不难发现，堆的结构完全被打乱了，因此此种方法是不合适的。那么有没有较好的方法能够删除堆顶数据，而又不打乱堆的结构呢?

答案是有的，我们只需:

1.先将堆顶数据和最后一个数据进行交换  2.删除尾部数据  3.对堆顶数据进行向下调整算法(稍后介绍)

 执行第一步以后，我们发现根节点被替换为12，虽然堆结构暂时被破坏了，但是根节点的左右子树仍维持着堆结构，此时我们要时整体结构仍为堆，便要引入向下调整算法。

---

---

-向下调整算法

向下调整算法需要一个父节点parent，此处为根节点 12 ，并计算出其左右子节点 5 和 2 ，然后比较左右子节点大小，选取其中一个子节点(小堆为子节点较小值，大堆为子节点较大值，此处为较小值 2 ) ，将此子节点与父节点进行比较，若不满足堆结构条件则交换。然后将此子节点位置作为parent，继续计算出其左右子节点......直到计算出的左右子节点均超过数组范围，即向下调整结束。

对于此堆，1. 取 5  和 2 的较小值 2 ，和父节点 12 交换，并将下标为2的位置作为父节点继续向下调整，此时其数据为 12 。2.取 9  和 3 的较小值 3 ，和父节点 12 进行交换.....此时父节点更新为下标为6的位置，计算其子节点超过范围，则向下调整结束。

 如图，调整完毕后，其结构满足堆结构。

下面进行代码实现:

void AdjustDown(HPDataType* a, size_t size)
{
	assert(a);
	size_t parent = 0;
	size_t child = parent*2 + 1;
	while (child < size)
	{
		//兄弟比较大小，取小为child
		if (child + 1 < size && a[child] > a[child + 1])
		{
			child = child + 1;
		}

		//父子比较，决定是否交换
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
		}
		else
		{
			break;
		}

		parent = child;
		child = parent * 2 + 1;
	}
	
}

与上文逻辑相同，此处难点是如何确定目标子节点。 parent从根节点开始，我们假设目标子节点为左子节点child1 = parent*2+1，当左子节点在数组范围之内时进入循环(反之则代表child均超过范围，向下调整结束)。进入循环后，如果child + 1(即右子节点)没超过范围 且 a[child+1] < a[child]，则说明右子节点为目标子节点，更新目标子节点child = child + 1。

此时child必为目标子节点，然后再与parent结点比较，若a[child] >= a[parent]，则满足堆结构，直接跳出循环，向下调整结束。否则进行Swap交换，并更新parent为child，并计算新的child值即可。直到child>=size，child超过范围，跳出循环，向下调整结束。

---

---

介绍完向下调整算法后，堆的删除函数便也很简单了，代码实现如下:

void HeapPop(Heap* hp)
{
    // 断言防止空指针
	assert(hp);
    // 断言确保有数据可删
	assert(hp->_size > 0);
    // 1.头尾数据交换
	Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);
    // 尾删
	hp->_size--;
    // 向下调整
	AdjustDown(hp->_a,hp->_size);

}

堆的数据插入和删除可谓是堆的实现的关键。其他函数实现与顺序表类似，实现也较为简单，此处不再过多介绍，下面上代码。

3.取堆顶的数据-HeapTop函数

HPDataType HeapTop(Heap* hp)
{
	assert(hp);
	assert(hp->_size > 0);
	return hp->_a[0];
}

4.取堆的数据个数-HeapSize函数

int HeapSize(Heap* hp)
{
	assert(hp);
	return hp->_size;
}

5.堆的判空(判断是否为空，若是返回真，反之则返回假)-HeapEmpty函数

int HeapEmpty(Heap* hp)
{
	assert(hp);
	return hp->_size == 0;
}

6.堆的销毁-HeapDestroy函数

void HeapDestory(Heap* hp)
{
	assert(hp);
	free(hp->_a);
	hp->_a = NULL;
	hp->_size = hp->_capacity = 0;
}

堆的实现到此结束！如有错误，欢迎指正。