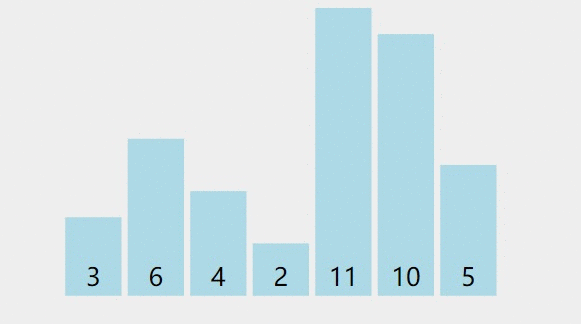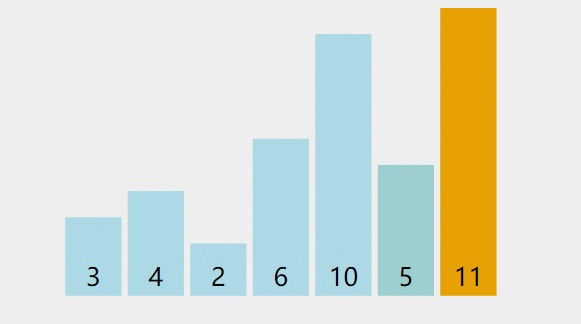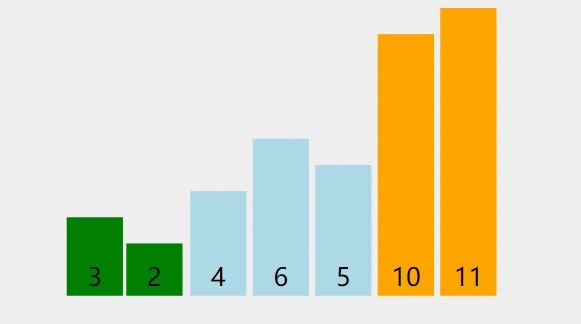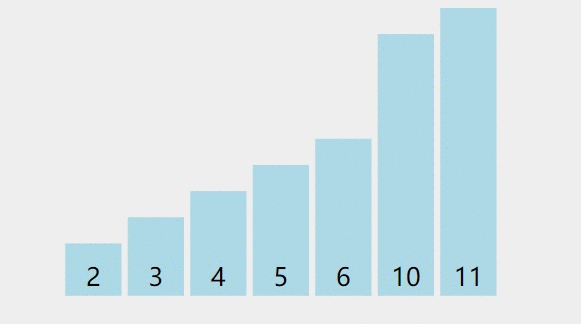排序算法：冒泡排序及优化

一、冒泡排序思想

  冒泡排序是交换排序的一种，交换排序和快速排序都属于基础排序算法

  冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序有误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端，故名“冒泡排序”

算法实现

---

• 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

---

实例图解

---

---

动画演示

---

二、冒泡排序实现及改进

冒泡排序基础版

算法描述：

• 第一轮：从上往下扫描数组的N个元素，先比较第一对相邻元素，如果逆序（第一个元素大于第二个元素）则交换，使大元素上移，再比较第二对相邻元素，如果逆序则仍交换，以此类推，经过第一轮处理，大元素慢慢上移，而最大的元素被移到最后的位置上，这也是它最终应该在的位置。
• 第二轮：对于无序区的N-1个元素，仍然是从第一对相邻元素到最后一对相邻元素依次比较，如果逆序就交换，与第一轮不同的是，少比较了一对，结果使第二大的元素被移到倒数第二位置上，这也是排序后它的最终位置。
• …

代码实现：

//基于数组的冒泡排序
#define _CRT_SECURE_NO_WARNINGS
#include 
#define MAXSIZE 20
void Input(int r[], int n);//输入数组的n个元素
void Output(int r[], int n);//输出数组的n个元素
void BubbleSort(int r[], int n);//冒泡排序(升序)
void Swap(int* a, int* b);//交换a和b所指变量的值 

int main(void)
{
    int a[MAXSIZE];//定义大小为MAXSIZE的数组
    int len;//定义数组的长度
    printf("请输入数组的长度为：\n");
        scanf("%d", &len);
    printf("输入数组的%d个元素：\n", len);
    Input(a, len);//输入数组的N个元素 
    printf("排序前数组a的元素为：");
    Output(a, len);//输出排序前数组的元素
    BubbleSort(a, len);//冒泡排序
    printf("排序后数组a的元素为：");
    Output(a, len);
    return 0;
}
void Input(int r[], int n)
{
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &r[i]);
    }
}
void Output(int r[], int n)
{
    for (int i = 0; i < n; i++)
    {
        printf("%d ", r[i]);
    }
    printf("\n");
}
void Swap(int* a, int* b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}
void BubbleSort(int r[], int n)
{
    for (int i = 1; i < n; i++)
    {
        for (int j = 0; j <= n - 1 - i; j++)
        {
            if (r[j] > r[j + 1])
            {
                Swap(&r[j], &r[j + 1]);
            }
        }
    }
}

结果演示：

---

冒泡排序优化1

优化思想：
如果在原始冒泡排序的后边几轮已经不需要排序了，但是按照原先的排序算法，还是要进行执行，针对这种情况进行改进，增加一个判断的变量 flag = 1（第1次必须扫描，初始值为1） ，在每轮排序前将flag重置为0，如果该轮排序有元素发生交换，那么会将flag 变为 1；否则flag=0;表示排序完成，终止排序即可。

实例演示：
优化1到底是怎么回事呢，先看个例子：未排序前的数据如图所示

有8个数组成一个无序数列：5，8，6，3，9，2，1，7，希望从小到大排序。按照冒泡排序的思想，我们要把相邻的元素两两比较，根据大小来交换元素的位置，过程如下：

首先让5和8比较，发现5比8要小，因此元素位置不变。

接下来让8和6比较，发现8比6要大，所以8和6交换位置。


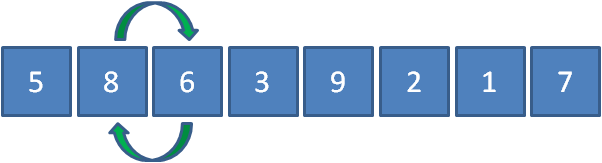
继续让8和3比较，发现8比3要大，所以8和3交换位置。


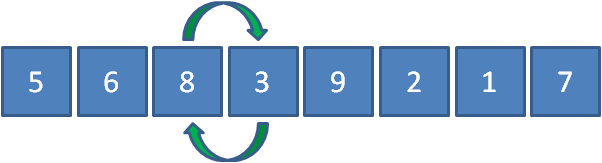
继续让8和9比较，发现8比9要小，所以元素位置不变。

接下来让9和2比较，发现9比2要大，所以9和2交换位置。


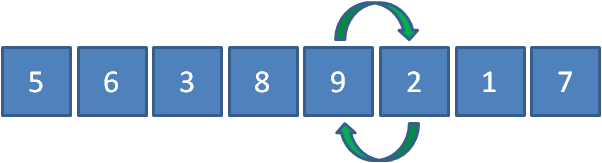
接下来让9和1比较，发现9比1要大，所以9和1交换位置。


最后让9和7比较，发现9比7要大，所以9和7交换位置。


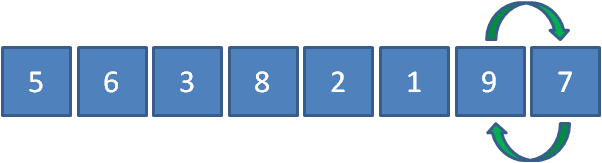
这样一来，元素9作为数列的最大元素，就像是汽水里的小气泡一样漂啊漂，漂到了最右侧。

这时候，我们的冒泡排序的第一轮结束了。数列最右侧的元素9可以认为是一个有序区域，有序区域目前只有一个元素。

第二轮排序结束后，我们数列右侧的有序区有了两个元素，顺序如下：

至于后续的交换细节，我们这里就不详细描述了，第三轮过后的状态如下：

第四轮过后状态如下：

第五轮过后状态如下：

第六轮过后状态如下：

第七轮过后状态如下（已经是有序了，所以没有改变）：

第八轮过后状态如下（同样没有改变）：

很明显可以看出，自从经过第六轮排序，整个数列已然是有序的了。可是我们的排序算法仍然“兢兢业业”地继续执行第七轮、第八轮。

这种情况下，如果我们能判断出数列已经有序，并且做出标记，剩下的几轮排序就可以不必执行，提早结束工作。

动画演示：

代码实现：

#define _CRT_SECURE_NO_WARNINGS
#include 
#define MAXSIZE 20
void Input(int r[], int n);//输入数组的n个元素
void Output(int r[], int n);//输出数组的n个元素
void BubbleSort(int r[], int n);//冒泡排序(升序)
void Swap(int* a, int* b);//交换a和b所指变量的值 
int main(void)
{
    int a[MAXSIZE];//定义大小为MAXSIZE的数组
    int len;//定义数组的长度
    printf("请输入数组的长度为：\n");
    scanf("%d", &len);
    printf("输入数组的%d个元素：\n", len);
    Input(a, len);//输入数组的N个元素 
    printf("排序前数组a的元素为：");
    Output(a, len);//输出排序前数组的元素
    BubbleSort(a, len);//冒泡排序
    printf("排序后数组a的元素为：");
    Output(a, len);
    return 0;
}
void Input(int r[], int n)
{
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &r[i]);
    }
}
void Output(int r[], int n)
{
    for (int i = 0; i < n; i++)
    {
        printf("%d ", r[i]);
    }
    printf("\n");
}
void BubbleSort(int r[], int n)
{
    int flag = 1;//设置flag为某轮是否有元素交换的标记，有交换则其值为1，否则为0，保证第1次必须扫描，初始值为1 
    for (int i = 1; flag && i < n; i++)//控制轮数,在某一轮排序结束后如果flag=0，则表示整个数组的排序完成，不再循环
    {
        flag = 0;
        for (int j = 0; j <= n - 1 - i; j++)//每一轮对于无序序列进行比较 
        {
            if (r[j] > r[j + 1])
            {
                Swap(&r[j], &r[j + 1]);
                flag = 1;
            }
        }
        printf("第%d轮排序结果：", i);
        Output(r, n);
    }
}
void Swap(int* a, int* b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;

结果演示：

---

冒泡排序优化2

优化思想：
优化一仅仅适用于连片有序而整体无序的数据(例如：1， 2，3 ，4 ，7，6，5)。但是对于前面大部分是无序而后边小半部分有序的数据(1，2，5，7，4，3，6，8，9，10)排序效率也不可观，对于种类型数据，我们可以继续优化。既我们可以记下最后一次交换的位置，后边没有交换，必然是有序的，然后下一次排序从第一个比较到上次记录的位置结束即可。

实例演示：
为了说明问题，咱们这次找一个新的数列：

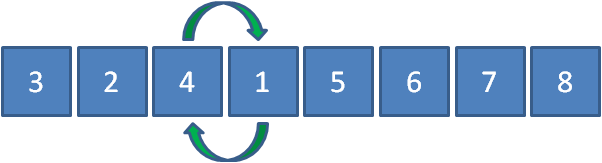
这个数列的特点是前半部分（3，4，2，1）无序，后半部分（5，6，7，8）升序，并且后半部分的元素已经是数列最大值。

让我们按照冒泡排序的思路来进行排序，看一看具体效果：

第一轮

元素3和4比较，发现3小于4，所以位置不变。

元素4和2比较，发现4大于2，所以4和2交换。


元素4和1比较，发现4大于1，所以4和1交换。


元素4和5比较，发现4小于5，所以位置不变。

元素5和6比较，发现5小于6，所以位置不变。

元素6和7比较，发现6小于7，所以位置不变。

元素7和8比较，发现7小于8，所以位置不变。

第一轮结束，数列有序区包含一个元素：

第二轮
元素3和2比较，发现3大于2，所以3和2交换。


元素3和1比较，发现3大于1，所以3和1交换。


元素3和4比较，发现3小于4，所以位置不变。

元素4和5比较，发现4小于5，所以位置不变。

元素5和6比较，发现5小于6，所以位置不变。

元素6和7比较，发现6小于7，所以位置不变。

元素7和8比较，发现7小于8，所以位置不变。

第二轮结束，数列有序区包含一个元素：

按照逻辑，有序区的长度和排序的轮数是相等的。比如第一轮排序过后的有序区长度是1，第二轮排序过后的有序区长度是2 ......

实际上，数列真正的有序区可能会大于这个长度，比如例子中仅仅第二轮，后面5个元素实际都已经属于有序区。因此后面的许多次元素比较是没有意义的。

我们可以在每一轮排序的最后，记录下最后一次元素交换的位置，那个位置也就是无序数列的边界，再往后就是有序区了。

代码实现：

//基于数组的冒泡排序
#define _CRT_SECURE_NO_WARNINGS
#include 
#define MAXSIZE 20
void Input(int r[], int n);//输入数组的n个元素
void Output(int r[], int n);//输出数组的n个元素
void BubbleSort(int r[], int n);//冒泡排序（升序）
void Swap(int* a, int* b);//交换a和b所指变量的值 
int main(void)
{
    int a[MAXSIZE];//定义大小为MAXSIZE的数组
    int len;//定义数组的长度
    printf("请输入数组的长度为：\n");
    scanf("%d", &len);
    printf("输入数组的%d个元素：\n", len);
    Input(a, len);//输入数组的N个元素 
    printf("排序前数组a的元素为：");
    Output(a, len);//输出排序前数组的元素
    BubbleSort(a, len);//冒泡排序
    printf("排序后数组a的元素为：");
    Output(a, len);
    return 0;
}
void Input(int r[], int n)
{
    for (int i = 0; i < n; i++)
    {
        scanf("%d", &r[i]);
    }
}
void Output(int r[], int n)
{
    for (int i = 0; i < n; i++)
    {
        printf("%d ", r[i]);
    }
    printf("\n");
}
void BubbleSort(int r[], int n)
{
    int lastSwapIndex = n - 1;//lastSwapIndex初始化为数组r最后数据下标
    for (int i = 1; lastSwapIndex > 0; i++)
    {
        int temp = -1;//每次进行排序前temp值重置为-1， 
        for (int j = 0; j < lastSwapIndex; j++)
        {
            if (r[j] > r[j + 1])
            {
                Swap(&r[j], &r[j + 1]);
                temp = j;
            }
        }
        printf("第%d轮排序数据：", i);
        Output(r, lastSwapIndex + 1);//输出本轮扫描的元素以及交换后的结果 
        lastSwapIndex = temp;//本轮最后一对交换前面一个元素下标赋值给lastSwapIndex
    }
}
void Swap(int* a, int* b)
{
    int temp;
    temp = *a;
    *a = *b;
    *b = temp;
}

结果演示：

---

三、冒泡排序性能分析

时空复杂度

• 时间复杂度：冒泡排序在平均和最坏情况下的时间复杂度都是O(n^2)，最好情况下都是O(n)；
• 空间复杂度：O(1)；

排序稳定性

稳定性：冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。所以，如果两个元素相等，是不必再去交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

参考资料：冒泡排序算法优化