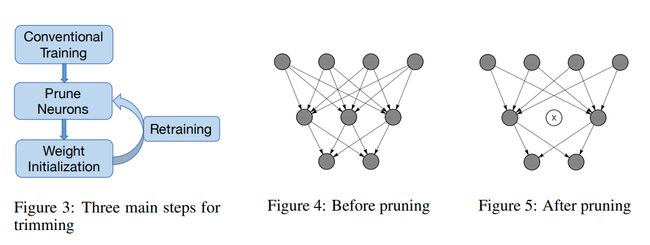
模型轻量化操作——剪枝
1. 剪枝基本概念
1.1 什么是剪枝 Network Pruning
1.2 剪枝的不同粒度
- 从单个神经元和连接到整个网络层
- 非结构化剪枝(需要特殊硬件支持) 权重级别(Fine-gained) sparsity 0-D
- 向量级别(介于二者之间) Sparsity 1-D
- 结构化剪枝(卷积核Kernel 特征图Featuremap) (不需要特殊硬件支持) 卷积核级别 Sparsity 2-D | 通道级别 Sparsity 3-D
1.3 模型剪枝
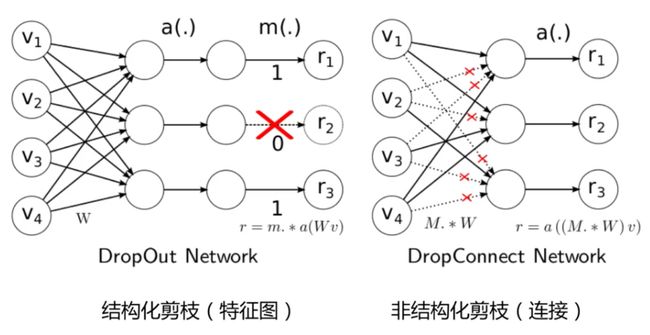
- Dropout 类似结构化剪枝 剪去神经元
- DropConnect 类似非结构化剪枝 (剪去连接)
只是训练的时候用一下,测试的时候不会用的,所以不是剪枝的方法
1.3.2 权重的冗余性
我们之所以能够对模型进行剪枝,本质上还是网络中的一些参数是冗余的,我们删除一些并不会对网络造成很大的影响,所以才可以去剪枝。
[1] Shang W, Sohn K, Almeida D, et al. Understanding and improving convolutional neural networks via concatenated rectified linear units[C]//international conference on machine learning. PMLR, 2016: 2217-2225.
卷积核存在相位互补性,需要同时学习两个线性相关的变换(CReLU)
不同层的统计特性
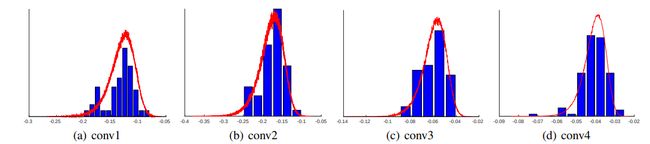
假设卷积核为 ϕ \phi ϕ,我们在神经网络中的任一层任取一个卷积核 ϕ j \phi_j ϕj,假设可以求一个 ϕ i \phi_i ϕi,使得其内积最小(方向相反),那么此时就得到一个新的向量:
ϕ i ˉ = arg min ϕ j < ϕ i , ϕ j > \bar{\phi_i} = \argmin_{\phi_j} <\phi_i, \phi_j> ϕiˉ=ϕjargmin<ϕi,ϕj>
理想状态下, ϕ i ˉ \bar{\phi_i} ϕiˉ 其实是和 ϕ j \phi_j ϕj相反的向量,此时我们在该神经网络层中除了 ϕ j \phi_j ϕj外剩下的卷积核中找一个与 ϕ i ˉ \bar{\phi_i} ϕiˉ相似度最小的 ϕ i \phi_i ϕi,做内积
μ i ϕ = < ϕ i , ϕ i ˉ > \mu_i^{\phi} = <\phi_i, \bar{\phi_i}> μiϕ=<ϕi,ϕiˉ>
画出 μ i ϕ \mu_i^{\phi} μiϕ分布的直方图
我们假设每一个 ϕ i \phi_i ϕi都能找到一个和它计算相似度越小并且非常接近于-1的值,那么µ的峰值应该越接近于-1(距离0值越远)。如果越找不到该值,它应该越接近于0。从上图可以看出,越是网络浅层,统计相似度越低,表明越有相位互补性;相反越往深层,越难找到和 ϕ i \phi_i ϕi相位相反的滤波器。
concatenated ReLU (CReLU)
C R e L U ( x ) = c o n c a t ( R e L U ( x ) , − R e L U ( x ) ) CReLU(x) = concat(ReLU(x), -ReLU(x)) CReLU(x)=concat(ReLU(x),−ReLU(x))

- 错误率降低, 也有可能是通道数提高了呀?
2. 非结构化剪枝
2.1 基本方法
[1] Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural network[J]. Advances in neural information processing systems, 2015, 28.
来看这片文章的例子:
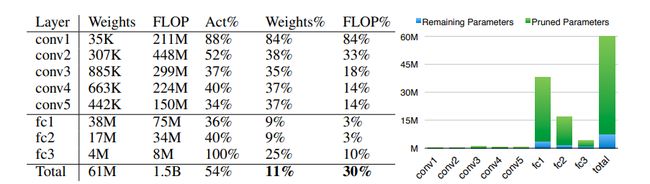
AlexNet 为例,右图是剪去的参数和保留的参数的对比,可以看到剪枝剪去的主要是全连接层的参数
卷积层与全连接层敏感性
是否微调,L1/L2范数对比
剪枝后微调很重要,绿线和紫线对比
L1/L2 都可做重要性因子,黄线和绿线基本重合

2.2 恢复权重法
对有些样本不重要,但是对另一些样本很重要(错误剪去一些连接从而导致模型的性能无法恢复)
[1] Guo Y, Yao A, Chen Y. Dynamic network surgery for efficient dnns[J]. Advances in neural information processing systems, 2016, 29.

和之前一样,先进行剪枝,之后再恢复(图三中的绿色箭头),对模型性能弥补有效
实现细节
- 实现一个掩膜矩阵 T T T,与权重矩阵大小相等
h k ( W j ( i , j ) ) = { 0 i f a k > ∣ W j ( i , j ) ∣ T k ( i , j ) o t h e r s 1 i f b k < ∣ W j ( i , j ) ∣ h_k(W_j^{(i,j)}) = \left\{\begin{matrix} 0 & if \ a_k > |W_j^{(i,j)}| & \\ T_k^{(i,j)} & others & \\ 1 & if \ b_k < |W_j^{(i,j)}| & \\ \end{matrix}\right. hk(Wj(i,j))=⎩ ⎨ ⎧0Tk(i,j)1if ak>∣Wj(i,j)∣othersif bk<∣Wj(i,j)∣
每一个元素表示是否减掉对应连接,当等于1表示保留,等于0表示剪枝,掩码为0的部分不参与损失计算,但是参数值仍然需要更新
(问:不收敛怎么办)
基本方案对比( AlexNet 模型)

基本方法:4800K次迭代,9倍压缩率
本方法:700K次迭代,17倍压缩率,训练更快
3. 结构化剪枝(幅度)
3.1 基于权重大小的通道裁剪
基于权重的范数剪掉卷积核
[1] Li H, Kadav A, Durdanovic I, et al. Pruning filters for efficient convnets[J]. arXiv preprint arXiv:1608.08710, 2016.ICLR2017
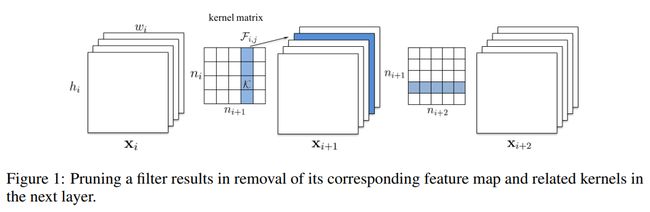
计算卷积核的绝对值和,进行排序,剪掉和最小的kernel以及对应的特征图
X i X_i Xi, X i + 1 X_{i+1} Xi+1和 X i + 2 X_{i+2} Xi+2 都是特征图
Kernel matrix 的共有 n i ∗ n i + 1 n_i * n_{i+1} ni∗ni+1个元素,每个元素是一个卷积核, X i X_i Xi通道数是 n i n_i ni, X i + 1 X_{i+1} Xi+1通道数是 n i + 1 n_{i+1} ni+1
实验结果
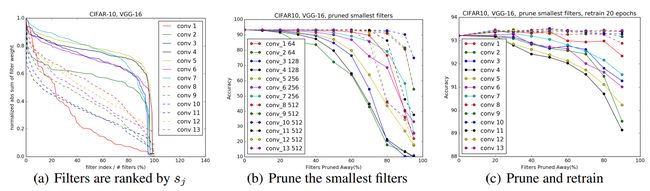
(b) 针对不同层的影响不同,比如最右边深蓝色虚线,剪枝到80%,依旧下降很少
© 剪枝之后retrain之后,部分层性能可以恢复,但是入黑色实线,性能无法恢复
最小幅度裁剪,随机幅度裁剪,最大幅度裁剪的不同
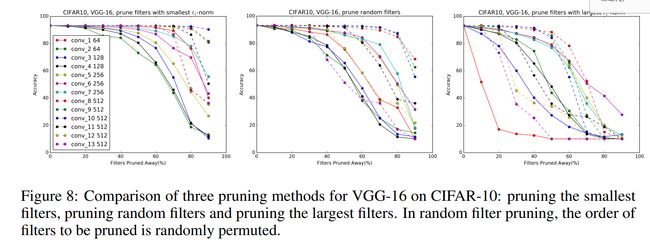
随机幅度裁剪与最小幅度裁剪效果相差不大,可以看出卷积核参数的冗余性
与特征图激活值裁剪方法比较
3.2 基于激活值的方法
基于激活的稀疏性,统计每一层的激活值为0的比例
Activated Percent of Zero
[1] Hu H, Peng R, Tai Y W, et al. Network trimming: A data-driven neuron pruning approach towards efficient deep architectures[J]. arXiv preprint arXiv:1607.03250, 2016.
A p o Z c ( i ) = A P o Z ( O c ( i ) ) = ∑ k N ∑ j M f ( O c , j ( i ) = 0 ) N × M ApoZ_{c}^{(i)} = APoZ( O_{c}^{(i)} ) = \frac { \sum^{N}_{k} \sum^{M}_{j} f(O_{c,j}^{(i)} = 0) } { N \times M } ApoZc(i)=APoZ(Oc(i))=N×M∑kN∑jMf(Oc,j(i)=0)
i i i表示层, c c c表示通道, N N N表示用于统计的样本数, M M M表示输出空间维度(xy合起来)
裁剪流程与非结构化剪枝的流程一样,不同的是,这里不是裁一个神经元,而是裁整个通道
VGG实验结果

单层裁剪结果:在不微调的情况下,即使裁剪了很多,模型效果也没有明显下降,证明了模型确实存在冗余现象
每个通道都可以建立一个 APoZ 值,说明APoZ变小了
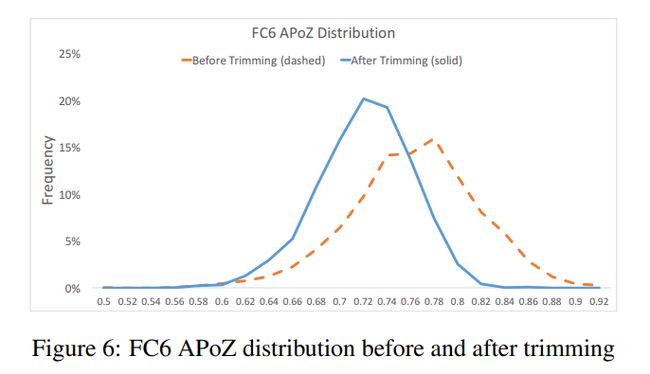
APoZ 用来判断参数的有效性
VGG多层裁剪结果

裁剪后效果下降很多,需要多次迭代来恢复到原来的效果
CONV45-FC67-trim-3 的意思是裁剪 CONV4 | CONV5 | FC6 | FC7 这几个层
4. 结构化剪枝(稀疏权重篇)
- 正则化与稀疏约束
- 稀疏约束框架
4.1 正则化与稀疏约束
正则化,权重衰减(其实就是L1/L2的范数惩罚)
J ~ ( ω ; X , y ) = J ( ω ; X , y ) + α 2 ∣ ∣ ω ∣ ∣ 2 J ~ ( ω ; X , y ) = J ( ω ; X , y ) + α ∣ ∣ ω ∣ ∣ 1 \tilde{J}(\omega; X, y) = J(\omega; X, y) + \frac{\alpha}{2} || \omega||_{2} \\ \tilde{J}(\omega; X, y) = J(\omega; X, y) + \alpha || \omega||_{1} J~(ω;X,y)=J(ω;X,y)+2α∣∣ω∣∣2J~(ω;X,y)=J(ω;X,y)+α∣∣ω∣∣1
L1约束相对于L2约束能够产生更加稀疏的模型,使得 ω \omega ω其中一些参数会变成0,也就是LASSO问题,常用于同时选择和缩减参数,可以用来模型剪枝
利用这个思想,再加一项,也就是 SSL
-
Structured Sparsity Learning(简称SSL)
E ( W ) = E D ( W ) + λ R ( W ) + λ g ∑ L l = 1 R g ( W ( l ) ) E(W) = E_{D}(W) + \lambda R(W) + \lambda_g \sum_{L}^{l=1} R_g(W^{(l)}) E(W)=ED(W)+λR(W)+λgL∑l=1Rg(W(l)) -
E D ( W ) E_{D}(W) ED(W) 是正常的损失项
-
R ( W ) R(W) R(W) 是非结构化正则项
-
R g ( W ( l ) ) R_g(W^{(l)}) Rg(W(l)) 是每一层的结构化正则项
R g ( W ( l ) ) = ∑ g = 1 G ∣ ∣ W ( g ) ∣ ∣ g R_g(W^{(l)}) = \sum_{g=1}^{G} || W^{(g)} ||_g Rg(W(l))=∑g=1G∣∣W(g)∣∣g 一组 W W W, Group Lasso
[1] Wen W, Wu C, Wang Y, et al. Learning structured sparsity in deep neural networks[J]. Advances in neural information processing systems, 2016, 29.
- 细粒度与粗粒度的稀疏化
Filter-wise(输出通道) 与 Channel-wise(输入通道)级别的稀疏化同时进行
∑ L l = 1 ( ∑ n l = 1 N l ∣ ∣ W n l , : , : , : ( l ) ∣ ∣ ) + ∑ L l = 1 ( ∑ c l = 1 C l ∣ ∣ W : , c l , : , : ( l ) ∣ ∣ ) \sum_{L}^{l=1} \left ( \sum_{n_l=1}^{N_l} || W_{n_l,:,:,:}^{(l)} || \right ) + \sum_{L}^{l=1} \left ( \sum_{c_l=1}^{C_l} || W_{:, c_l,:,:}^{(l)} || \right ) L∑l=1(nl=1∑Nl∣∣Wnl,:,:,:(l)∣∣)+L∑l=1(cl=1∑Cl∣∣W:,cl,:,:(l)∣∣)
- N l N_l Nl 表示输出通道数,每一组对应当前层某一个输出通道的所有相关卷积核
- C l C_l Cl 表示输入通道数,每一组对应若干卷积核,用于对输入的所有通道进行卷积,产生一个通道的输出结果
- 以上两者会相互耦合
所以最终的优化目标:
E ( W ) = E D ( W ) + λ n ∑ L l = 1 ( ∑ n l = 1 N l ∣ ∣ W n l , : , : , : ( l ) ∣ ∣ ) + λ c ∑ L l = 1 ( ∑ c l = 1 C l ∣ ∣ W : , c l , : , : ( l ) ∣ ∣ ) E(W) = E_{D}(W) + \lambda_n \sum_{L}^{l=1} \left ( \sum_{n_l=1}^{N_l} || W_{n_l,:,:,:}^{(l)} || \right ) + \lambda_c \sum_{L}^{l=1} \left ( \sum_{c_l=1}^{C_l} || W_{:, c_l,:,:}^{(l)} || \right ) E(W)=ED(W)+λnL∑l=1(nl=1∑Nl∣∣Wnl,:,:,:(l)∣∣)+λcL∑l=1(cl=1∑Cl∣∣W:,cl,:,:(l)∣∣)
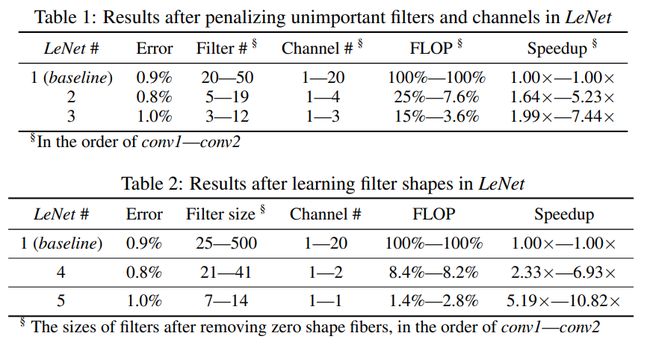
The optimization target of learning shapes of filers becomes:
E ( W ) = E D ( W ) + λ s ∑ l = 1 L ( ∑ c l = 1 C l ∑ m l = 1 M l ∑ k l = 1 K l ∣ ∣ W : , c l , m l , k l ( l ) ∣ ∣ ) E(W) = E_{D}(W) + \lambda_s \sum_{l=1}^{L} \left ( \sum_{c_l=1}^{C_l} \sum_{m_l=1}^{M_l} \sum_{k_l=1}^{K_l} || W_{:,c_l,m_l,k_l}^{(l)} || \right ) E(W)=ED(W)+λsl=1∑L(cl=1∑Clml=1∑Mlkl=1∑Kl∣∣W:,cl,ml,kl(l)∣∣)
MLP的稀疏化结果
AlexNet 稀疏化结果
会将卷积运算操作改为 GEneral Matrix Multiplication(GEMM),而 row-wise 和 column-wise 分别是卷积核和特征图


前两行是训练稀疏模型
第三行是剪枝
后两行是稀疏剪枝后再训练的结果
是一个基于学习的模型剪枝策略,其实并没有剪枝? 只是让一部分参数为0?
4. 结构化剪枝(稀疏因子篇)
- 基于BN缩放因子的方法
- 基于输出缩放因子的方法
4.1 基于BN缩放因子的稀疏性
Liu Z, Li J, Shen Z, et al. Learning efficient convolutional networks through network slimming[C]//Proceedings of the IEEE international conference on computer vision. 2017: 2736-2744.
Network Slimming,基于BN中的缩放因子 γ \gamma γ来对不重要的通道进行裁剪

不要求每个通道中的元素都有一个较小的激活值,约束更弱

优化目标:
L = ∑ ( x , y ) l ( f ( x , W ) , y ) + λ ∑ γ ∈ Γ g ( γ ) L = \sum_{(x,y)} \bm{l}(f(x, W), y) + \lambda \sum_{\gamma\in \Gamma} g(\gamma) L=(x,y)∑l(f(x,W),y)+λγ∈Γ∑g(γ)
其中 γ \gamma γ是BN中的 γ \gamma γ:
z ^ = z i n − μ B σ B 2 + ϵ ; z o u t = γ z ^ + β \hat{z} = \frac{ z_{in} - \mu_{B} } { \sqrt{ \sigma_{B}^2 + \epsilon } }; \ \ \ \ z_{out} = \gamma \hat{z} + \beta z^=σB2+ϵzin−μB; zout=γz^+β
不同模型的裁剪结果
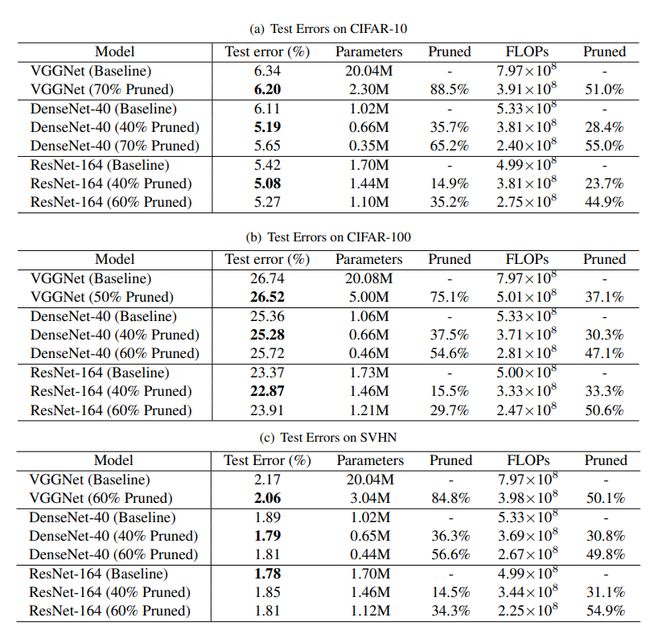
VGGNet中 γ = 1 0 − 4 \gamma=10^{-4} γ=10−4
DenseNet | ResNet 中 γ = 1 0 − 5 \gamma=10^{-5} γ=10−5
不同比例裁剪稀疏下的精度变换(DenseNet40, CIFAR10, λ = 1 0 − 5 \lambda=10^{-5} λ=10−5)
- 蓝色线是在红色线的基础上进行裁剪的,可以看到裁剪后retrain,可以有更大的裁剪比例
- 存在明显的阈值,低于该阈值裁剪影响不大,但是高于该阈值也无法恢复性能
- Trained with Sparsity 是啥?
不同稀疏权重下的尺度系数分布与变化趋势(VGGNet)

纵轴是 Scaling factor value 也就是 γ \gamma γ,显然,惩罚项系数 λ \lambda λ越大,最终的 γ \gamma γ越小
4.2 基于输出缩放因子的方法
比上一个方法更加通用,可以用到多种模型中
- Sparse Structure Selection,约束输出稀疏(可应用于通道,分组,残差块) 简称SSS
Huang Z, Wang N. Data-driven sparse structure selection for deep neural networks[C]//Proceedings of the European conference on computer vision (ECCV). 2018: 304-320.
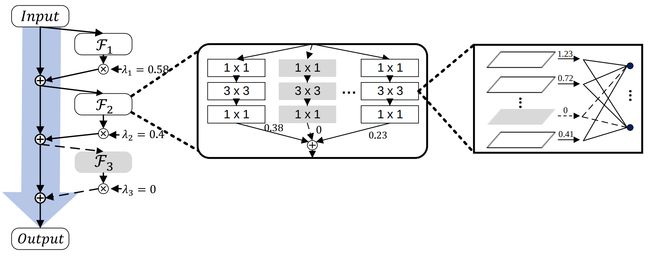
每一个 F i F_i Fi都有一个系数 λ i \lambda_i λi,优化目标:
min w , λ 1 N ∑ i = 1 N L ( y i , C ( x i , w , λ ) ) + R ( w ) + R s ( λ ) \min_{w, \lambda} \frac{1}{N} \sum_{i=1}^{N} L\left( y_i, C \left (x_i, w, \lambda \right ) \right) + R(w) + R_s(\lambda) w,λminN1i=1∑NL(yi,C(xi,w,λ))+R(w)+Rs(λ)
R s ( λ ) = γ ∣ ∣ λ ∣ ∣ 1 R_s(\lambda) = \gamma||\lambda||_{1} Rs(λ)=γ∣∣λ∣∣1
实验结果:
VGG(基于通道)
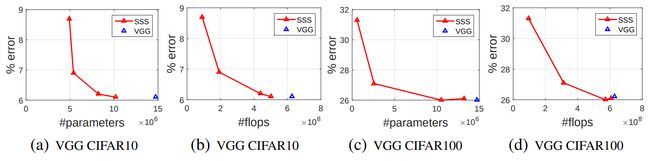
SSS == Sparse Structure Selection
ResNet(基于残差块)
向图片左下角表示更好

与SSL对比:SSS 不需要 finetune?
4. 结构化剪枝(重建篇)
- 基本方法
- 通道选择方法改进
Channel Pruning 框架
He Y, Zhang X, Sun J. Channel pruning for accelerating very deep neural networks[C]//Proceedings of the IEEE international conference on computer vision. 2017: 1389-1397.
- 直接裁剪输入通道B,维持输出通道C的精度不损失
根据输入特征图各种通道对输出贡献的大小来进行裁剪
通道从 c c c剪枝到 c ′ c' c′,剪枝之后,输出特征图 Y Y Y的信息能够维持
arg min β , W 1 N ∣ ∣ Y − ∑ i = 1 c ∣ ∣ β i X i W i T ∣ ∣ F 2 + λ ∣ ∣ β ∣ ∣ 1 \arg \min_{\beta, W} \frac{1}{N} || Y - \sum_{i=1}^{c} || \beta_i X_i W_i^T||_F^2 + \lambda || \beta ||_1 argβ,WminN1∣∣Y−i=1∑c∣∣βiXiWiT∣∣F2+λ∣∣β∣∣1
其中,
∣ ∣ β ∣ ∣ 0 ≤ c ′ , ∀ i ∣ ∣ W i ∣ ∣ F = 1 ||\beta||_0 \le c', \ \ \ \forall i || W_i ||_F = 1 ∣∣β∣∣0≤c′, ∀i∣∣Wi∣∣F=1
采集特征图 N × c × k h × k w N \times c\times k_h\times k_w N×c×kh×kw
对应Kernel n × c × k h × k w n\times c\times k_h\times k_w n×c×kh×kw
得到 N × n N\times n N×n的输出 Y Y Y
N N N表示样本, n n n表示输出通道数, X X X维度 N × k h k w N\times k_h k_w N×khkw, W W W维度 n × k h k w n\times k_h k_w n×khkw
通道选择改进
之前基于通道重建误差,没有考虑模型语义信息,没有考虑到真正对任务的影响,只是考虑了数值上的重建误差
通过在模型中间增加分支来辅助模型训练
Zhuang Z, Tan M, Zhuang B, et al. Discrimination-aware channel pruning for deep neural networks[J]. Advances in neural information processing systems, 2018, 31.

分P段进行剪枝,在各个阶段添加分支损失
首先是特征图重建loss L M L_M LM,辅助分类loss L S P L_S^P LSP,和最终的分类loss L f L_f Lf
- 用 L S P L_S^P LSP和 L f L_f Lf来进行微调 fine-tune
- 用 L S P L_S^P LSP 和 L M L_M LM来进行通道选择
那如何进行通道选择呢

将损失对每一个通道的梯度值作为重要性因子,逐渐将通道添加到集合 A A A( A c A^c Ac表示补集),更新权重,直到满足终止条件
min W L ( W ) , s . t . W A c = 0 \min_W \ \ L(W), \ \ s.t. \ \ W_{A^c} = 0 Wmin L(W), s.t. WAc=0
W A < = W A − γ ∂ L ∂ W A W_A <= W_A - \gamma \frac{ \partial L }{ \partial W_A } WA<=WA−γ∂WA∂L
终止条件是:
∣ L ( W t − 1 ) − L ( W t ) ∣ / L ( W 0 ) ≤ ϵ | L(W^{t-1}) - L(W^{t}) | / L(W^0) \le \epsilon ∣L(Wt−1)−L(Wt)∣/L(W0)≤ϵ
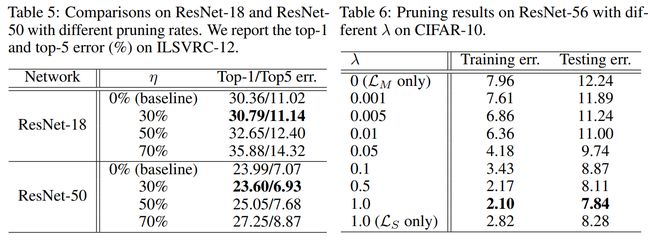
- η \eta η是剪枝率,剪枝剪到一个适当的比例,错误率可以下降,参数也可以减少
- 右表是 L ( W ) = L M ( W ) + λ L S p ( W ) L(W) = L_{M}(W)+\lambda L_{S}^{p}(W) L(W)=LM(W)+λLSp(W), λ \lambda λ取不同值时的效果,只有 L M L_M LM时是只有重建损失
ϵ \epsilon ϵ不同——不同的终止原则
最终再来个可视化
- (b) 是剪枝剪掉的通道
- © 是留下的通道,可以看到留下的通道响应值更明显