【最短路算法】一篇文章彻底弄懂Dijkstra算法|多图解+代码详解

• 博主简介：努力学习的大一在校计算机专业学生，热爱学习和创作。目前在学习和分享：算法、数据结构、Java等相关知识。
• 博主主页： @是瑶瑶子啦
• 所属专栏: 算法 ；该专栏专注于蓝桥杯和ACM等算法竞赛
• 近期目标：写好专栏的每一篇文章

一、简介

Dijkstra算法适用于最短路问题中，单源最短路（只有一个起点），并且每条边的权重都是正数的情况

二、基本思想策略

首先假定源点为u（就是起点），顶点集合V被划分为两部分：集合 S 和 V-S。 初始时S中仅含有源点u，其中S中的顶点到源点的最短路径已经确定。
集合S 和V-S中所包含的顶点到源点的最短路径的长度待定，称从源点出发只经过S中的点到达V-S中的点的路径为特殊路径（不一定是最短的）
并用dist[]记录当前每个顶点对应的最短特殊路径长度。

红色顶点是S集合中，均已经确定最短路径的点，而绿色的是V-S集合中没有确定该顶点到源点最短路径的点。我们可以看到只经过S中的点到绿色点有两条特殊路径：15+20和20+10，但是只有一条最短路径：15+20，那么绿色点就当前情况来看，可以暂时把它的dist[i]更新为25，但是一定是最短特殊路径吗？不一定，为什么呢？我们接下来往下看

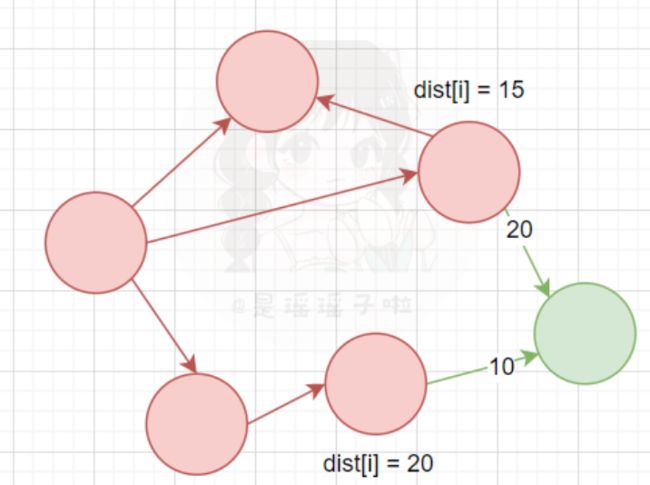
可以看到，V-S集合中假设存在一点T，经过这点到目的点的距离，很有可能是目的点真正的dist！

可能这里可能有点晕，没错。上面只是一个大概的介绍，我们接下来彻底揭开它的神秘面纱。

选择特殊路径长度最短的路径，将其连接的V-S中的顶点加入到集合S中，同时更新数组dist[]（核心）。一旦S包含了所有顶点，dist[]就是从源到所有其他顶点的最短路径长度。

数据结构: h[N],e[M],ne[M],w[M]构建带权重的邻接表，来存储图;int dist[N];//dist 数组保存源点到其余各个节点的距离

（1）初始化。令集合S={0}，对于集合V-S中的所有顶点x{1，2，3…n}；初始化dist数组memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大,

（2）找最小。在集合V-S中依照贪心策略来寻找使得dist[j]具有最小值的顶点t,即dist[t]=min，则顶点t就是集合V-S中距离源点u最近的顶点。
（3）加入S战队。将顶点t加入集合S，同时更新V-S
（4）借东风。在（2）中已近找到了源点到t的最短路径，那么对集合V-S中所有与顶点t相邻的顶点j，都可以借助t走捷径。
如果dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j]，转（2）。

光凭这个好像是这么回事，但是细节值得推敲。这个题的本质还是贪心。
比如只看刚刚的文字，不仔细分析，你能不能解决我开头提出的那个问题？
为什么这么说呢。因为在目前（局部情况）来看，确实找到最短特殊路径了，竟然就直接加入S战队，不太可取，就像我开头提出的，在V-S集合中，万一存在一个点，经过这个点再到目的点，很有可能才是真正的最短距离。
那为什么这个算法是可取的呢？
巧就巧在，最外层循环，遍历了整个顶点，并且并不是说，一旦该顶点加入了S战队，它的dist就不能变了，相反，它在实时更新！。当循环遍历到绿色顶点T时，会更新与它相连节点的dist。
不知道有没有get到我的意思，虽然我没有用公式啥的去推导，我个人也非常讨厌那种不人性化的方式，更喜欢用一种形象的，意会的方式去理解。

综上，由局部最优，到全局最优，这种贪心的策略，完全可以保证全部遍历和循环后，dist[]数组中存的就是该点到源点的最短距离！！！（上面是我个人的理解，欢迎一起讨论交流和学习捏！）

三、代码实现

这里是AcWing 849.Dijkstra求最短路 I模板题目

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

数据范围

1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。

3.1伪代码详解

int dist[N],state[N];
dist[1] = 0,state = 1;//把源点加入S集合
for (i : 1~n)
{
  1),t<-找最小，找到只经过S中的点到V-S集合中某一点，距离最小的那个V-S中的那个点
  2),state[t] = 1;将t加入到S战队
   3),更新与t顶点相邻点的dist
  
}

3.2源代码详解

#include
#include
#include

using namespace std;

//N是顶点数，M是边数
const int N =510,M = 100010;
int h[N],e[M],ne[M],w[M],idx;//邻接表存储图，w[M]存储边的权重
int state[N];//state记录是否找到了源点到该节点的最短距离
int dist[N];//dist保存源点到其余各个顶点的最短特殊距离
int n,m;//图的顶点数和边数

void add(int a,int b,int c)//插入边，并给每个边赋值权重
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a],h[a] = idx++;
}
//key:核心和关键部分！！！
void Dijkstra()
{
    memset(dist,0x3f,sizeof(dist));// 1)初始化dist数组
    
    dist[1] = 0;//源点到源点的距离当然是0
    
    for (int i = 0; i < n; i++)//对n个顶点进行n次遍历（一开始V-S集合为n个元素,S集合是0个，肯定是遍历n次，才能完全遍历完
    {
        int t = -1;//t存储当前这次遍历到的V-S集合中的点，该点当前局部情况距离源点距离最小的那个点
        //2)在V-S中 找最小
        for (int j = 1; j <= n; j++){
            if(!state[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        }
        state[t] = 1;//3)加入S 战队
        
        //3）借东风
        for (int j = h[t];j != -1; j = ne[j])
        {
            int i = e[j];
            dist[i] = min(dist[i],dist[t]+w[j]);//更新dist[j]
        }                                                    
    }
}

int main(){
    memset (h,-1,sizeof (h));//初始化邻接表
    
    cin >> n >>m;
    while (m--)//读入m条边
    {
        int a,b,w;
        cin >> a >> b >> w;
        add (a,b,w);
    }
    Dijkstra();
    if (dist[n] != 0x3f3f3f3f)//如果dist[n]被更新了，那么一定存在从1号节点到n号节点的最短距离路径
        cout << dist[n];
    else
        cout << "-1";
}

关于存储图的适合，没有考虑重边和自环的影响？

因为在第三步更新的时候，即使邻接表那条单链上有两个一样编号的节点，但是第三步更新的时候，还是会让对应编号节点的dist为最小。所以即使有重边也不影响

3.4：数据结构优化

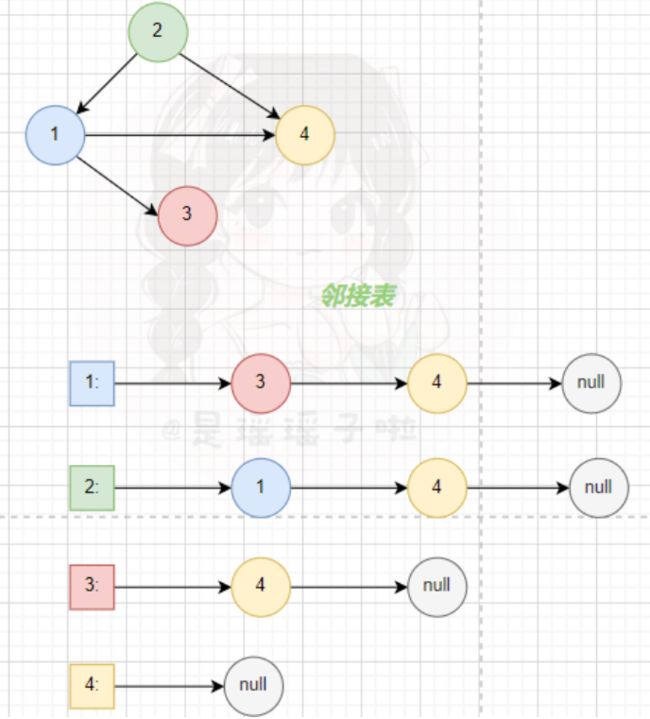
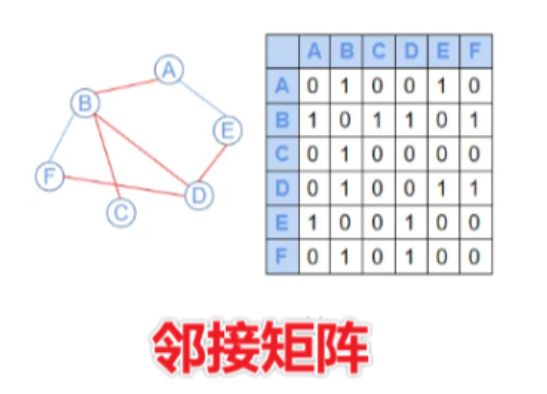
上面我们是采用邻接表来存储图，邻接表的原理如下。邻接表是适合稀疏图，当边比较多，也就是稠密图时，我们采用邻接矩阵来存储图。即g[a][b]的值为编号为a的节点a到编号为b的节点b之间的距离。

使用邻接矩阵，注意去重边，因为邻接矩阵只允许a→b的距离唯一。

#include 
#include 
#include 

using namespace std;

const int N = 510;

int n,m;

int g[N][N];//邻接矩阵存储图
int dist[N];
bool st[N];

int dijkstra(){
    memset(dist,0x3f,sizeof(dist)); 
    
    dist[1] = 0;
    
    for(int i = 0; i < n; i++){
        int t = -1;
        for (int j = 1; j <= n; j ++)
            if (!st[j] && (t == -1|| dist[t] > dist[j]))
                t = j;
        
        st[t] = true;
        
        for (int j = 1; j <= n; j++)
            dist[j] = min(dist[j],dist[t] + g[t][j]);
        
    }
    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main(){
    scanf("%d%d",&n,&m);
    memset(g,0x3f,sizeof g);//初始化邻接矩阵
    
    while(m--){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g[a][b] = min(g[a][b],c);//去除重边
    }
    int t = dijkstra();
    
    printf("%d\n",t);
    
    return 0;
}

3.3：算法分析

算法时间复杂度：时间复杂是 O(n2+m)O(n2+m), n 表示点数，m表示边数

耗时的主要地方在于第2)步，找最小，每次都需要遍历一遍dist数组，完全没有必要。可以使用小根堆来优化（小根堆的数据结构可以自己来实现（推荐），或者用库中的）

四、使用小根堆来优化Dijkstra算法

这个定义的heap，完全可以看作集合V-S的具体化！通过这个小根堆，可以直接取出（取出+删除）V-S集合的最小值。

#include 
#include 
#include 
#include //堆的头文件

using namespace std;

typedef pair<int, int> PII;//堆里存储距离和节点编号

const int N = 1e6 + 10;

int n, m;//节点数量和边数
int h[N], w[N], e[N], ne[N], idx;//邻接表存储图
int dist[N];//存储距离
bool st[N];//存储状态

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆
    heap.push({0, 1});//插入距离和节点编号

    while (heap.size())
    {
        auto t = heap.top();//取距离源点最近的点
        heap.pop();

        int ver = t.second, distance = t.first;//ver:节点编号，distance:源点距离ver 的距离

        if (st[ver]) continue;//如果距离已经确定，则跳过该点
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});//距离变小，则入堆
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

使用小根堆后，找到 t 的耗时从 O(n^2) 将为了 O(1)。每次更新 dist 后，需要向堆中插入更新的信息。所以更新dist的时间复杂度有 O(e) 变为了 O(elogn)。总时间复杂度有 O(n^2) 变为了 O(n + elongn)。适用于稀疏图。

五、深入和反思

最开始我们说到，Dijkstra算法只适用于边的权重都是正数的情况。为什么负权边不行呢？

看一个Dijkstra算法失效的例子：

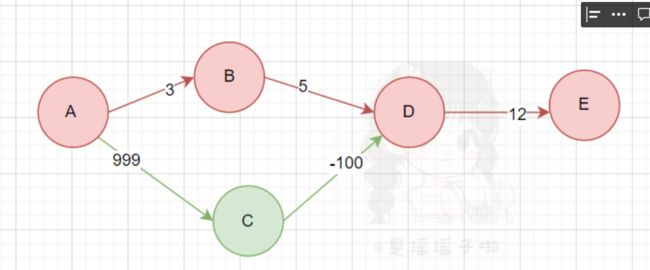
A→B→D→E，确定dist[E]=20，dist[D]=8

然后A→C→D虽然更新了D点的dist，使之正确dist[D]=-1,但是由于D已经被遍历过，无法通过D来更新E，导致最终求出的A→E的最小距离出错。

为什么呢？

D的dist的正确性不受负权的影响，是因为负权指向的是D，在更新节点，更新dist的时候，会更新掉D的错误值。但E就不一样了，在当前局部，只有D一个经过它，D一旦遍历过后，更新了E。当经过C到D时，无法再通过正确的D去更新E！

如果全部是正值的话，在A→D时，能一下子确定当前真正的dist[D]！再dist[D]+12，那dist[E]也是正确的！

所以根本原因在于，存在负权边，dist[D]的真值不能在更新dist[E]之前确定。

最后是我个人总结的理解：

在Dijkstra算法视角，把B遍历并进行相关更新后，它当前得知了如下情况：dist[A] = 0,dist[B] = 2,dist[D] = 5,dist[C] = 999,dist[D] = 999+C,C>0,Dijkstra当然会放弃A-C-D这条路，可是C其实<0,这条路不该被放弃，反而A-C-D的路径长度很有可能会小于A-B-C的长度，正是由于Dijkstra的这点输入，导致出现负权边时，结果不正确，再说，人家的正确性本来就是建立在所有边的权重都>0的基础上！

---

• Java岛冒险记【从小白到大佬之路】
  
• LeetCode每日一题–进击大厂
• 算法