代码随想录算法训练营第天十五天丨 二叉树part03

文档讲解：代码随想录

状态：已完成

104.二叉树的最大深度 

思路

递归法

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

用后序遍历（左右中）来计算树的高度。

具体思路在代码注释中。

class Solution {
    public int maxDepth(TreeNode root) {
        //递归法
        return getHeight(root);
    }
    //递归三部曲
    //1.确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
    int getHeight(TreeNode root){
        //2.确定终止条件：如果为空节点的话，就返回0，表示高度为0。
        if(root == null){return 0;}//当结点为 null 时，当前结点的高度为 0 
        //3.确定终止条件：如果为空节点的话，就返回0，表示高度为0。
        //深度遍历 - 后序遍历 左右中
        
        //左
        int left = getHeight(root.left);
        //右
        int right = getHeight(root.right);
        //中
        return (right > left ? right : left) + 1;
    }
}

---

111.二叉树的最小深度

思路

直觉上好像和求最大深度差不多，其实还是差不少的。

本题依然是后序遍历，【前序求的是深度，后序求的是高度】。

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。

以下讲解中遍历顺序上依然采用后序遍历（因为要比较递归返回之后的结果）。

本题还有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解，如图：

题目中说的是：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。，注意是叶子节点。

什么是叶子节点，左右孩子都为空的节点才是叶子节点！

#递归法

递归三部曲:

1. 确定递归函数的参数和返回值
2. 确定终止条件
3. 确定单层递归的逻辑

对于第三点 确定单层递归的逻辑，这块和求最大深度不一样，很多人会写成

int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int result = 1 + min(leftDepth, rightDepth);
return result;

知识将返回的时候由取最大值改为取最小值

这个代码就犯了此图中的误区：

如果这么求的话，没有左孩子的分支会算为最短深度。

所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

class Solution {
    public int minDepth(TreeNode root) {
        //递归三部曲
        return getMinHeight(root);
    }
    //1.确定递归函数的参数和返回值
    //参数为要传入的二叉树根节点，返回的是int类型的深度。
    int getMinHeight(TreeNode node){
        //2.确定终止条件
        //终止条件也是遇到空节点返回0，表示当前节点的高度为0。
        if (node == null){return 0;}
        //3.确定单层递归的逻辑
        //这块和求最大深度可就不一样了
        int left = getMinHeight(node.left);
        int right = getMinHeight(node.right);
        if (node.left == null && node.right != null){
            return 1 + right;
        }
        if (node.left != null && node.right == null){
            return 1 + left;
        }
        return 1 + (left > right ? right : left);
    }
}

---

222.完全二叉树的节点个数

思路

普通二叉树

这道题目其实刚看的时候，想着毫不犹豫选择层序遍历直接写，按照昨天的层序遍历模板做一些改动，加一个变量result，统计结点数量就行。

递归遍历的顺序依然是后序（左右中）。

层序遍历：

class Solution {
    // 迭代法
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        Queue queue = new LinkedList<>();
        queue.offer(root);
        int result = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size -- > 0) {
                TreeNode cur = queue.poll();
                result++;
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return result;
    }
}

完全二叉树

以上方法都是按照普通二叉树来做的，对于完全二叉树特性不了解可以看这篇 关于二叉树，你该了解这些！ (opens new window)，这篇详细介绍了各种二叉树的特性。

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。

举一个典型的例子如题：

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

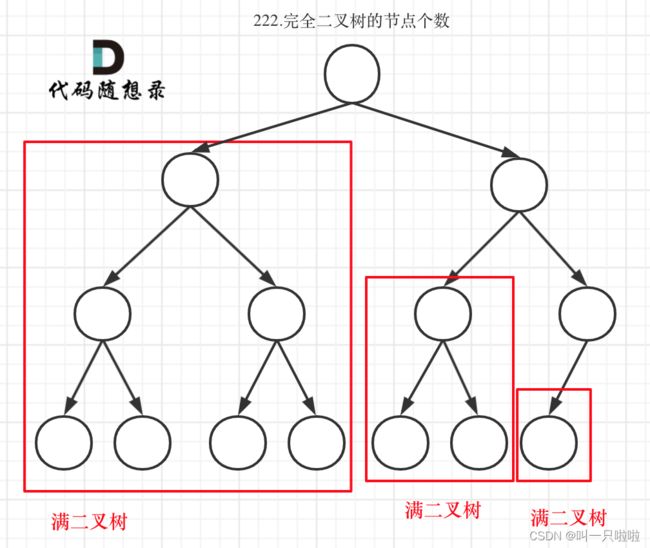
完全二叉树（一）如图：

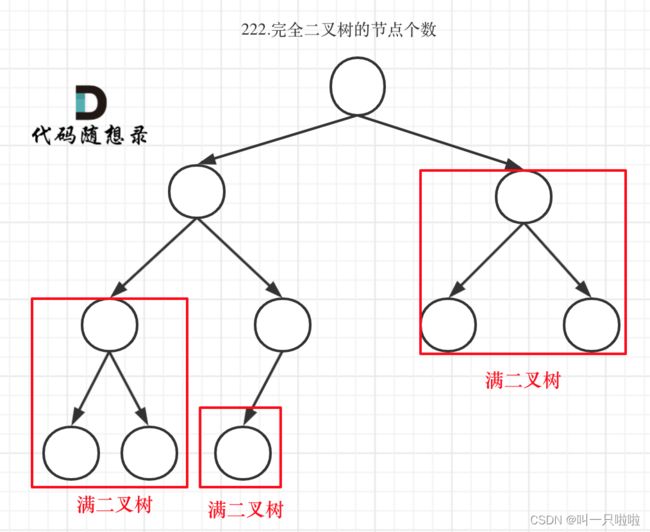
完全二叉树（二）如图：

可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

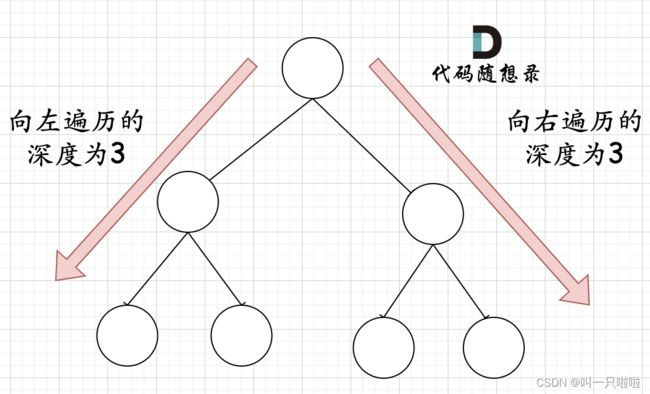
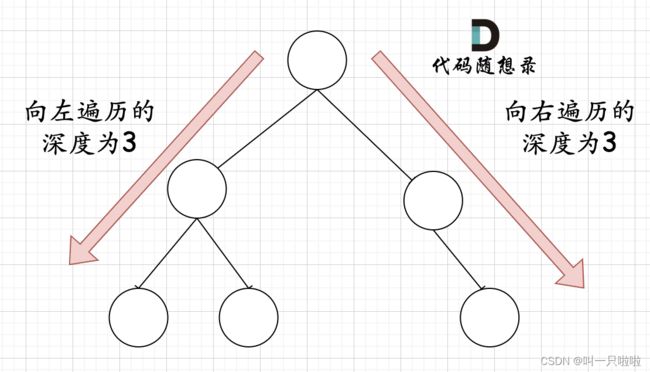
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

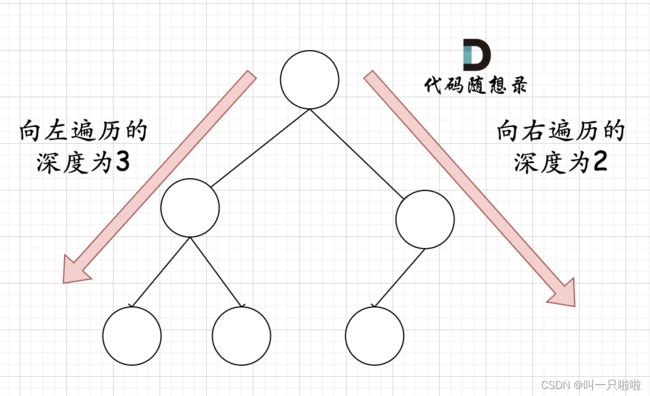
在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：

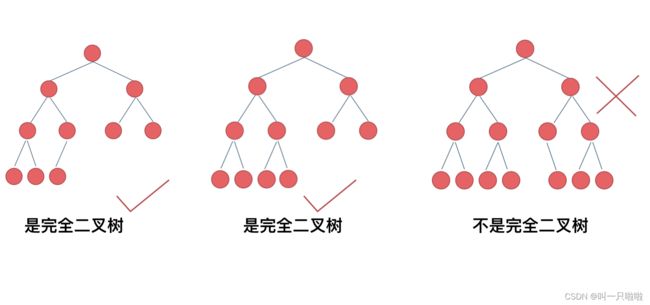
这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题：

如果这么想，大家就是对 完全二叉树理解有误区了，以上这棵二叉树，它根本就不是一个完全二叉树！

判断其子树是不是满二叉树，如果是则利用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归.

class Solution {
    public int countNodes(TreeNode root) {
        return getNum(root);
    }
    int getNum(TreeNode node){
        //第二部：终止条件的写法应该是这样的：
        if (node == null){return 0;}
        TreeNode leftNode = node.left;
        TreeNode rightNode = node.right;
        int leftCount = 0;
        int rightCount = 0;
        while (leftNode != null){
            leftNode = leftNode.left;
            leftCount++;
        }
        while (rightNode != null){
            rightNode = rightNode.right;
            rightCount++;
        }
        if (leftCount == rightCount){
            return (2 << leftCount) - 1;// // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量
        }
        //第三部，单层递归的逻辑：（可以看出使用后序遍历）
        int left = getNum(node.left);
        int right = getNum(node.right);
        return left + right + 1;
    }
}

---

以上为我做题时候的相关思路，自己的语言组织能力较弱，很多都是直接抄卡哥的，有错误望指正。