数据结构基础9:排序全家桶
排序全家桶:
- 一:插入排序:
-
- 1.简单插入排序:
- 2.希尔排序:
- 二:选择排序:
-
- 1.简单选择排序:
- 2.堆排序(空间复杂度为O(1)):
- 三:快速排序;
-
- 方法一:Hoare
-
- ==修改一==:
- ==修改二:==
- 方法二:挖坑法:
- 方法三:前后指针法:
- 方法四:非递归实现快速排序:
-
- 1.结构体存储范围:
- 2.直接存储数据:
- 方法五:小区间优化:
- 四:归并排序。
-
- 方法一:递归排序
- 方法二:非递归排序:
- 五:计数排序:
-
- 方法一:
- 六:总结:
一:插入排序:
1.简单插入排序:
1.一次的插入排序主要做的是:将end插入前面[0,end-1]已经有顺序的里面。
1-1:我们需要先去保存当前的end位置的数值为tmp:
1-2:tmp和[0,end-1]范围的数据去比较:
1-3:假设我们是升序:如果当前的数值比tmp大说明这个位置的数据可以向后移动:
1-4:end需要–向前面寻找直到满足:
1-4-1:end为0的时候,我们就直接结束循环说明这个tmp放置到开头:
1-4-1:end不是0的时候但是前面的数值比tmp小,结束循环说明这个数值已经到了合适的位置:
2.注意只有一个数值的时候一个数值自然有序:
3.循环遍历前面2个,3个,4个,5个……………………直到数组中的所有数值被排序完成:
//1.简单插入排序:
void Insertqsort(int* arr, int n)
{
int i = 0;
while (i < n-1)
{
//防止end越界:
int end = i + 1;
int tmp = arr[end];
while (end > 0)
{
//排升序:
if (arr[end - 1] > tmp)
{
arr[end] = arr[end - 1];
end--;
}
else
{
break;
}
}
arr[end] = tmp;
i++;
}
}
2.希尔排序:
1.希尔排序和简单插入排序的区别就是:
1-1:我们可以更加快速的进行数值移动让数组更快的有序:
2.我们的简单插入排序的数据都是在一起一次移动1步,我们希尔排序让数据分成多个组别每一个组别之间进行数值的移动:
3.我们有两个分组的方式:
3-1:gap=gap/2
3-2:gap=gap/3+1
4.控制好区间和每次移动的数值就可以:
//2.希尔排序:
void ShellQsort(int* arr, int n)
{
int gap = n;
//gap为1的时候进行的就是简单插入排序结果一定有顺序:
while (gap >= 1)
{
gap = gap / 2;
int i = 0;
while (i < n - gap)
{
int end = i + gap;
int tmp = arr[end];
while (end >= gap)
{
if (arr[end - gap] > tmp)
{
arr[end] = arr[end - gap];
end -= gap;
}
else
{
break;
}
}
arr[end] = tmp;
i++;
}
}
}
二:选择排序:
1.简单选择排序:
1.控制范围找到当前范围的数值最大和最小记录下标:
2并且把下标的数值进行交换:
2-1:注意如果最大的数值就在范围的最左边在小的值交换完成之后会发现最大的数值就跑到之前最小的数值的位置了:
2-2:在这样的情况下需要进行下标的修正:
3.缩小范围继续寻找最大和最小。
//2.选择排序:
void SelectQsort(int* arr, int n)
{
int left = 0;
int right = n - 1;
while (left < right)
{
int min = left;
int max = left;
int i = left;
while (i <= right)
{
if (arr[min] > arr[i])
{
min = i;
}
if (arr[max] < arr[i])
{
max = i;
}
i++;
}
swap(&arr[min], &arr[left]);
if (max == left)
max = min;
swap(&arr[max], &arr[right]);
left++;
right--;
}
}
2.堆排序(空间复杂度为O(1)):
1.为什么说是一个空间复杂度为O(1)因为这个排序在原来的空间的基础上就完成了排序:
2.在一定的范围里面进行向下建堆,可以从第一个叶子节点到跟节点去一个一个向下调整建堆。
2-1:可以从根节点到最后一个节点去建堆但是:
2-3:从叶子开始时间复杂度是O(N)
2-4: 从根节点开始到结尾需要时间复杂度:O(N*longN)
3.建好一个堆之后就进行数据的交换(第一个数据和最后一个数据进行交换效果就是把最大的数值拿到最后并且之后的操作都不会影响这个数据:)并且把需要建立堆的范围减少。
void AdjustDown(int* arr, int n)
{
int num = n;
while (n >= 0)
{
//1.从第一个非叶子节点开始:
int parent = (n - 1) / 2;
int chart = parent * 2 + 1;
while (chart <= n)
{
if (chart + 1 <= n)
{
chart = arr[chart] < arr[chart + 1] ? chart + 1 : chart;
}
//进行交换:
if (arr[chart] > arr[parent])
{
swap(&arr[chart], &arr[parent]);
}
else
{
//1.不满足交换条件就直接跳出去不调整了:
break;
}
parent = chart;
chart = parent * 2 + 1;
}
n--;
}
}
//4.堆排序:
void HeapQsort(int* arr, int n)
{
int num = n;
while (--num)
{
AdjustDown(arr, num);
//已经是一个大堆:
swap(&arr[0], &arr[num]);
}
}
三:快速排序;
1.快速排序是Hoare在1962年提出的一种通过二叉树结构衍生出的一种交换排序方法。
2/主要思路是在数组中选出一个数值作为基准值,按照这个基准值(排序是升序还是降序)进行数值的交换和移动。
3.操作完成后形成了这个基准值已经到了正确的位置。
4.左右两个范围继续上面的步骤,进入递归。
5.当范围中只有一个数值的时候就可以返回结束这个递归因为一个数自然有序。
//5:快速排序:
void QuickSort(int* a, int left , int right)
{
if (left >= right)
return;
int centre = partsort1(a, left, right);
//[0,centre-1] centre [centre+1 , right];
//进入递归:
QuickSort(a, left, centre - 1);
QuickSort(a, centre + 1, right);
}
下面都是排一个升序:
方法一:Hoare
1.确定一个key作为我们的基准值是一个数值不是下标,我们保存一个keyi作为我们基准值的下标。
2.左和右同时开弓右边找比key小的,右边找比key大的。
3.进行交换—当左右的相遇说明已经遍历了一遍把key对应值的位置和相遇点进行交换这个时候就让key这个值到了合适的位置。
4.为什么最后这个位置满足了和keyi的交换条件因为这个位置是比key小的(R先移动造成的)?
4-1:相遇:
4-1-1:R动L不动,相遇满足点的数值大于key
4-1-2:L动R不动,相遇满足点的数值小于key
4-2:移动问题:考虑上一次的移动:
4-2-1:R先移动,这个时候L因为上一次的交换L位置的值是小于key的
4-2-2:R先移动中间有一个小于key的值,就停下来,L再移动。再这个位置停下来:
int PartSort1(int* a, int left, int right)
{
int key = a[left];
int keyi = left;
while (left < right)
{
//1.右先动找小:
while (left < right && a[right] > key)
{
right--;
}
//找到比key小的停止了:
//2.左动找大
while (left < right && a[left] < key)
{
left++;
}
//找到比key大的值了:
swap(&a[left], &a[right]);
}
swap(&a[keyi], &a[left]);
return left;
}
修改一:
1.问题一:找到的数值和key的数值相等就不跳过。
1-1:如果出现右边先找到相等的值了,左边再找又找到相等的值了。这个时候进行交换是没有意义的并且下一次进入函数(右找)直接认为是找到,左边认为是找到了,这样就会进入死循环。
int PartSort1(int* a, int left, int right)
{
int key = a[left];
int keyi = left;
while (left < right)
{
//1.右先动找小:
while (left < right && a[right] >= key)
{
right--;
}
//找到比key小的停止了:
//2.左动找大
while (left < right && a[left] <= key)
{
left++;
}
//找到比key大的值了:
swap(&a[left], &a[right]);
}
swap(&a[keyi], &a[left]);
return left;
}
修改二:
1.如果我们拿左值作为key那么如果数组的值比较有序我们从右边开始找都找不到比key小的值right都已经到负的下标然后left还没有动。
2.归根结底是key值在这个数组中不是一个比较偏中间的位置:
3.改正方法:三数取中和交换到left
int getmin(int* a, int left, int right)
{
int min = (left + right) / 2;
if (a[left] < a[right])
{
if (a[min] < a[left])
return left;
else if (a[right] < a[min])
return right;
else
return min;
}
else if (a[left] > a[right])
{
if (a[min] > a[left])
return left;
else if (a[right] > a[min])
return right;
else
return min;
}
}
//5-1:Hoare法
int PartSort1(int* a, int left, int right)
{
int centre = getmin(a, left, right);
swap(&a[centre], &a[left]);
int key = a[left];
int keyi = left;
while (left < right)
{
//1.右先动找小:
while (left < right && a[right] >= key)
{
right--;
}
//找到比key小的停止了:
//2.左动找大
while (left < right && a[left] <= key)
{
left++;
}
//找到比key大的值了:
swap(&a[left], &a[right]);
}
swap(&a[keyi], &a[left]);
return left;
}
方法二:挖坑法:
1.定义一个key保存我们比较中间的数值:
2.定义一个keyi保存坑的下标:
3.坑的更新:
3-1R先移动找比key小的值找到之后把数值直接赋值到对应的坑位,把坑位更新成当前的位置。
3-2:L再移动找比key大的值把数值直接赋值到对应的坑位,把坑位更新成当前的位置。
3-3:当R和L相遇了这个坑位就是给我们的key这个值留着的:
//5-2:挖坑法:
// 挖坑法
int PartSort2(int* a, int left, int right)
{
int mid = getmin(a, left, right);
swap(&a[mid], &a[left]);
int key = a[left];
int keyi = left;
while (left < right)
{
while(left < right && a[right] >= key)
{
right--;
}
//1.填原来的坑:
a[keyi] = a[right];
//2.更新坑的位置:
keyi = right;
while(left < right && a[left] <= key)
{
left++;
}
//1.填原来的坑:
a[keyi] = a[left];
//2.更新坑的位置:
keyi = left;
}
a[keyi] = key;
return left;
}
方法三:前后指针法:
1.定义一个cur和prev去遍历我们的数组:
2.cur找比key小的数值,++prev交换数值:
3移动过程:
3-1:开始的时候cur还没有遇到比key大的数值的时候prev是紧紧跟着cur,prev的相对的数值就是比key小的。
3-2:cur遇到比key大的数值进行移动的过程这个时候prev不需要移动。
3-3:当cur再一次遇到了比key小的数值就++prev进行交换。
3-4:为什么要++prev因为没有++之前是小于key的但是因为cur出去的条件是因为遇到了比key大的值所以++prev的这个位置的值就是比key大的满足交换条件。
4.当cur出去数组的时候,这个时候prev对应的位置就是一个小于key值可以和之前保存的值进行交换:
//5-3:前后指针:
//5-3:前后指针:
int PartSort3(int* a, int left, int right)
{
int mid = getmin(a, left, right);
swap(&a[mid], &a[left]);
int prev = left;
int cur = prev +1;
int keyi = left;
while (cur <= right)
{
//相同位置就不交换
//当cur找到比a[keyi]小的值就交换:
if (a[cur] < a[keyi] && ++prev!=cur)
{
swap(&a[prev],&a[cur] );
}
cur++;
}
//没有++prev所以位置的值是小于a[keyi]的值的,
//所以可以交换值到前面去是满足位置条件。
swap(&a[prev], &a[keyi]);
return prev;
}
方法四:非递归实现快速排序:
1.我们的递归思路是一个先序遍历的一种操作把左和右调整好。把key放在合适的位置。
2.进行深度优先遍历的一个过程。
3.我们递归建立栈帧然后通过实参带给形参我们的这个范围。
4.我们通过栈这一个数据结构保存我们的数据,这样可以保证对一颗树有序之后才去排另一颗树。
1.结构体存储范围:
typedef struct range {
int left;
int right;
}rg;
typedef rg Stackinttype;
typedef struct Stack {
Stackinttype* a;
int top;
int capacity;
}ST;
//6.快速排序的非递归实现:
void QuickSort_NOT(int* a, int left, int right)
{
ST Quick;
StInit(&Quick);
while (left <= right)
{
int being = left;
int end = right;
int mid = getmin(a, being, end);
swap(&a[mid], &a[being]);
int prev = being;
int cur = prev + 1;
int keyi = being;
while (cur <= end)
{
//相同位置就不交换
//当cur找到比a[keyi]小的值就交换:
if (a[cur] < a[keyi] && ++prev != cur)
{
swap(&a[prev], &a[cur]);
}
cur++;
}
//没有++prev所以位置的值是小于a[keyi]的值的,
//所以可以交换值到前面去是满足位置条件。
swap(&a[prev], &a[keyi]);
int centre = prev;
rg range_left = { left,centre - 1 };
rg range_right = { centre + 1 , right };
//1.放数据:
StPush(&Quick, range_left);
StPush(&Quick, range_right);
//2.拿数据:
rg tmp = StTop(&Quick);
StPop(&Quick);
left = tmp.left;
right = tmp.right;
}
StDestroy(&Quick);
}
2.直接存储数据:
//6.快速排序的非递归实现:
void QuickSort_NOT(int* a, int left, int right)
{
ST Quick;
StInit(&Quick);
while (left <= right)
{
int being = left;
int end = right;
int mid = getmin(a, being, end);
swap(&a[mid], &a[being]);
int prev = being;
int cur = prev + 1;
int keyi = being;
while (cur <= end)
{
//相同位置就不交换
//当cur找到比a[keyi]小的值就交换:
if (a[cur] < a[keyi] && ++prev != cur)
{
swap(&a[prev], &a[cur]);
}
cur++;
}
//没有++prev所以位置的值是小于a[keyi]的值的,
//所以可以交换值到前面去是满足位置条件。
swap(&a[prev], &a[keyi]);
int centre = prev;
//1.放数据:
StPush(&Quick, left);
StPush(&Quick, centre - 1);
StPush(&Quick, centre + 1);
StPush(&Quick, right);
//2.拿数据:
right = StTop(&Quick);
StPop(&Quick);
left = StTop(&Quick);
StPop(&Quick);
}
StDestroy(&Quick);
}
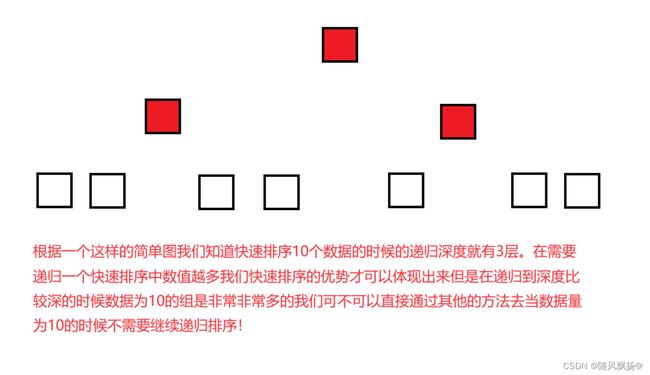
方法五:小区间优化:
1.如果我们需要排序一个10个数据的一个数组使用快速排序的递归的化感觉不是特别值,有没有什么方法可以在10个及以下数据把他排出来呢?
2.我们可以在递归调用到数据为10的时候去使用一个插入排序去提高代码效率。
//6-2:快速排序小区间优化:
void QuickSort_Minimun(int* a, int left, int right)
{
//1.进入递归优化:
if (right - left + 1 > 10)
{
int centure = PartSort3(a,left, right);
QuickSort_Minimun(a, left, centure - 1);
QuickSort_Minimun(a, centure+1,right);
}
//2.进入插入排序优化:如果你在递归到一定程度之后
//你的数组的首元素的地址的位置是不一样的。
//是需要进行移动的!!!
else if(right - left + 1 <= 10)
{
Insertqsort(a+left, right - left + 1);
return;
}
}
四:归并排序。
方法一:递归排序
主要思路:
1.我们想让左边有序和右边有序然后在一起合并。
2.左边有序就需要左边的左边有序和左边的右边有序在一起归并右边同理。
3.直到左边和右边都只有一个了进入一个合并两个有序数组的操作就可以!
4.我们这个排序是一个时间复杂度:O(N*longN) 空间复杂度是O(N).
5.建立一个tmp在str的相同位置去保存归并好的这一个范围的结果,然后再拷贝回去,解决如果原地归并的数值覆盖问题!
6.总结这是一个后序遍历操作是再递归回去的过程中进行的一个比较插入拷贝回去的一个过程。
//7-1;归并排序——递归内容:
void _MergeSort(int* str,int* tmp, int left , int right)
{
//基本上是相等的情况回去 (1 1)
if (left >= right)
return;
int centre = (left + right) / 2;
//进入递归左右:
_MergeSort(str, tmp, left, centre);
_MergeSort(str, tmp, centre+1,right);
//到最深的时候进行的一系列操作:
int cur = left;
int being1 = left;
int being2 = centre + 1;
//1.比较插入:有一个结束就结束了!
while (being1<=centre && being2<=right)
{
if (str[being1] <= str[being2])
{
tmp[cur++] = str[being1++];
}
else if (str[being1] > str[being2])
{
tmp[cur++] = str[being2++];
}
}
//2.判断是否结束的继续插入,存在有一个数组没有插入完全的情况:
while (being1 <= centre)
{
tmp[cur++] = str[being1++];
}
while (being2 <= right)
{
tmp[cur++] = str[being2++];
}
//3.拷贝回去:
memcpy(str + left, tmp + left, sizeof(int)*((right - left) + 1));
}
方法二:非递归排序:
1我们递归进入1个和1个数值之间的归并,通过递归返回进行2,2归并以此类推到整体有序。
2.非递归的方法定义gap为1从1,1个到2个2个进行归并……这作为一个循环进行归并但是这样的情况只适用于2的次方的个数元素的情况。
void _MergeSort_Not(int* str, int* tmp,int centre, int left, int right)
{
int cur = left;
int being1 = left;
int being2 = centre + 1;
//1.比较插入:有一个结束就结束了!
while (being1 <= centre && being2 <= right)
{
if (str[being1] <= str[being2])
{
tmp[cur++] = str[being1++];
}
else if (str[being1] > str[being2])
{
tmp[cur++] = str[being2++];
}
}
//2.判断是否结束的继续插入,存在有一个数组没有插入完全的情况:
while (being1 <= centre)
{
tmp[cur++] = str[being1++];
}
while (being2 <= right)
{
tmp[cur++] = str[being2++];
}
//3.拷贝回去:
memcpy(str + left, tmp + left, sizeof(int) * ((right - left) + 1));
}
//7-2;归并排序——非递归内容:
void MergeSort_Not_1(int* str, int* tmp, int left, int right)
{
//1.如果不去借用递归回去的过程去比较插入拷贝排序的话
//直接从1,1,-》2,2…………这样一个过程去排序
int gap = 1;
while (gap <= ((right - left + 1) / 2))
{
int cur = left;
while (cur<=right-gap)
{
_MergeSort_Not(str, tmp,cur + gap -1,cur,cur+2*gap-1);
cur += 2 * gap;
}
gap *= 2;
}
}
//7-3-1:优化:
void _MergeSort_Not_end(int* str, int* tmp, int centre, int left, int right ,int sum)
{
int cur = left;
int beging1 = left, end1 = centre;
int beging2 = centre + 1, end2 = right;
//1,范围修正,堆区空间开辟的问题。
if (end2 > sum)
{
end2 = sum;
}
while (beging2 <= sum &&(beging1 <= end1 && beging2 <= end2))
{
if (str[beging1] < str[beging2])
{
tmp[cur++] = str[beging1++];
}
else if(str[beging1] >= str[beging2])
{
tmp[cur++] = str[beging2++];
}
}
//2.判断是否结束的继续插入,存在有一个数组没有插入完全的情况:
while ( beging1 <= end1)
{
tmp[cur++] = str[beging1++];
}
while ( beging2 <= end2)
{
tmp[cur++] = str[beging2++];
}
memcpy(str + left, tmp + left, (sizeof(int)*(cur-left)));
}
//7-3;归并排序——非递归内容(优化非2的次方情况):
void MergeSort_Not_1(int* str, int* tmp, int left, int right)
{
//1.如果不去借用递归回去的过程去比较插入拷贝排序的话
//直接从1,1,-》2,2…………这样一个过程去排序
int gap = 1;
while (gap <= right - left)
{
int cur = left;
while (cur <= right - gap)
{
_MergeSort_Not_end(str, tmp, cur + gap - 1, cur, cur + 2 * gap - 1,right-left);
cur += 2 * gap;
}
gap *= 2;
}
}
//7:归并排序——非递归。
void MergeSort_Not(int* str, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc file\n");
exit(-1);
}
MergeSort_Not_1(str, tmp, 0, n-1);
free(tmp);
tmp = NULL;
}
五:计数排序:
方法一:
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中:
//8-1:计数排序:
void CountSort(int* a, int n)
{
//1.找最大和最小:
int min = 0, max = 0;
for (int i = 0; i < n; i++)
{
if (min > a[i])
{
min = a[i];
}
if (max < a[i])
{
max = a[i];
}
}
int range = (max - min + 1);
//2.创建count数组
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
perror("malloc file\n");
exit(-1);
}
//3:遍历数据记录个数:
//初始化为全部0:
memset(count, 0, range * sizeof(int));
for (int j = 0; j < n; j++)
{
count[(a[j] - min)]++;
}
int l = 0;
//4:遍历count去改变a数组:
for (int k = 0; k < range; k++)
{
int num = count[k];
while (num--)
{
a[l] = (k + min);
l++;
}
}
}
六:总结:
总结文章链接: