LeetCode刷题——树(python语言)
LeetCode刷题——树(python语言)
一、树
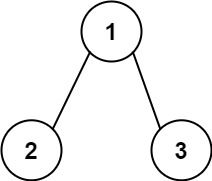
数其实就是链表的拓展,将链表的后指针的一个跟改为多个。树已经不是线性结构了。其中最为经典的就是二叉树。如下图所示,即为一个二叉树。其中1为根节点,2为左子树,3为右子树。遍历树的方法与图类似,有深度优先搜索(DFS),利用栈来存储节点(后进先出),和广度优先搜索(BFS),利用队列来存储节点(先进先出)。二叉树的遍历方法最经典有三种,分为先序(根左右),中序(左根右)和后序(左右根),遍历主要采用递归的方法,一颗子树一般遍历结束回溯。
二、刷题
2.1 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
解法一:利用DFS(深度优先搜索),每次向下遍历,深度加一。
- 设置变量temp记录当前节点深度
- 将temp作为DFS函数参数传递到子节点
- 程序第一次“进入”节点后更新temp
- “进入”空节点时说明完成一条路径的遍历,更新结果ans
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def DFS(self,root: Optional[TreeNode],temp:int,ans:int):
if not root:
self.ans = max(temp,self.ans)
return
temp = temp + 1
self.DFS(root.left,temp,self.ans)
self.DFS(root.right,temp,self.ans)
return
def maxDepth(self, root: Optional[TreeNode]) -> int:
self.ans = 0
temp = 0
self.DFS(root,temp,self.ans)
return self.ans
解法二:DFS后序遍历,遍历左右结点后,加上根节点的深度,以此递归
- 程序遇到空节点时,返回空节点的高度0给父节点
- 程序第三次“进入”节点时,其两个子节点的最大高度都已计算出来并返回给了该节点
- 根据子节点的最大高度可以计算出来当前节点的最大高度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def DFS(self,root: Optional[TreeNode]):
if not root:
return 0
left = self.DFS(root.left)
right = self.DFS(root.right)
ans = max(left,right) + 1
return ans
def maxDepth(self, root: Optional[TreeNode]) -> int:
ans = self.DFS(root)
return ans
解法三:BFS(广度优先搜索),每遍历一层,深度加一
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
ans = 0
q = []
q.append(root)
while(root and len(q)):
ans += 1
size = len(q)
for i in range(size):
cur = q.pop(0)
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
return ans
2.2 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 的二叉树。
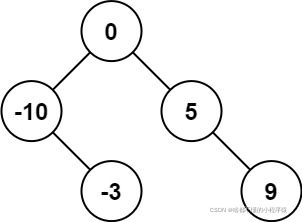
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
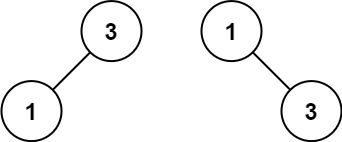
输入:nums = [1,3]
输出:[3,1]
解释:[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildBST(self,nums:List[int],low:int,high:int):
if low>high:
return None
mid = (low+high)//2
root = TreeNode(nums[mid])
root.left = self.buildBST(nums,low,mid-1)
root.right = self.buildBST(nums,mid+1,high)
return root
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
low,high = 0,len(nums)-1
return self.buildBST(nums,low,high)
2.3 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:2

示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
提示:
树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000
DFS:
首先可以想到使用深度优先搜索的方法,遍历整棵树,记录最小深度。
对于每一个非叶子节点,我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题,可以递归地解决该问题。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
if not root.left and not root.right:
return 1
min_depth = 10**9
if root.left:
min_depth = min(self.minDepth(root.left), min_depth)
if root.right:
min_depth = min(self.minDepth(root.right), min_depth)
return min_depth + 1
#476 ms 55.7 MB
同样,我们可以想到使用广度优先搜索的方法,遍历整棵树。
当我们找到一个叶子节点时,直接返回这个叶子节点的深度。广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小。
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
que = collections.deque([(root, 1)])
while que:
node, depth = que.popleft()
if not node.left and not node.right:
return depth
if node.left:
que.append((node.left, depth + 1))
if node.right:
que.append((node.right, depth + 1))
return 0
#384 ms 51.8 MB
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/solution/er-cha-shu-de-zui-xiao-shen-du-by-leetcode-solutio/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
2.4 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
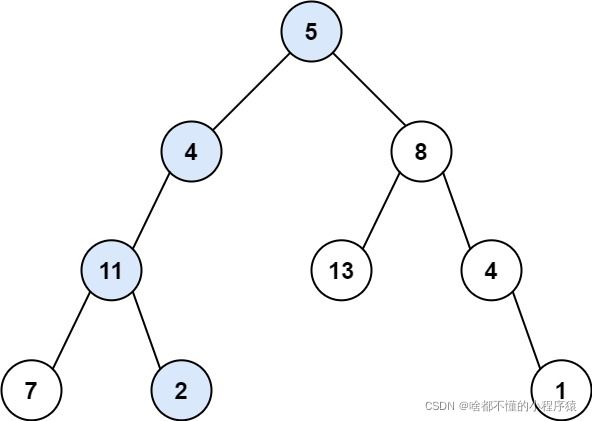
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:
return False
s = [(root, root.val)] # elem: (node, node.val)
while s:
node, valSum = s.pop()
if not node.left and not node.right:
if valSum == targetSum:
return True
continue
if node.left:
s.append((node.left, node.left.val + valSum))
if node.right:
s.append((node.right, node.right.val + valSum))
return False
BFS
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root:
return False
que_node = collections.deque([root])
que_val = collections.deque([root.val])
while que_node:
now = que_node.popleft()
temp = que_val.popleft()
if not now.left and not now.right:
if temp == sum:
return True
continue
if now.left:
que_node.append(now.left)
que_val.append(now.left.val + temp)
if now.right:
que_node.append(now.right)
que_val.append(now.right.val + temp)
return False
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/path-sum/solution/lu-jing-zong-he-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
递归
观察要求我们完成的函数,我们可以归纳出它的功能:询问是否存在从当前节点 root 到叶子节点的路径,满足其路径和为 sum。
假定从根节点到当前节点的值之和为 val,我们可以将这个大问题转化为一个小问题:是否存在从当前节点的子节点到叶子的路径,满足其路径和为 sum - val。
不难发现这满足递归的性质,若当前节点就是叶子节点,那么我们直接判断 sum 是否等于 val 即可(因为路径和已经确定,就是当前节点的值,我们只需要判断该路径和是否满足条件)。若当前节点不是叶子节点,我们只需要递归地询问它的子节点是否能满足条件即可。
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/path-sum/solution/lu-jing-zong-he-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: TreeNode, sum: int) -> bool:
if not root:
return False
if not root.left and not root.right:
return sum == root.val
return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)
2.5 二叉搜索树迭代器
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字,则返回 true ;否则返回 false 。
int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
输入
[“BSTIterator”, “next”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]
解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False
提示:
树中节点的数目在范围 [1, 105] 内
0 <= Node.val <= 106
最多调用 105 次 hasNext 和 next 操作
进阶:
你可以设计一个满足下述条件的解决方案吗?next() 和 hasNext() 操作均摊时间复杂度为 O(1) ,并使用 O(h) 内存。其中 h 是树的高度。
采用栈来存储元素。利用栈的后进先出的特性,实现DFS。对于二叉树,先让根节点入栈,将根节点的左子树都入栈,向右遍历。弹出当前节点,然后遍历右子树。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class BSTIterator:
def __init__(self, root: TreeNode):
self.stack = []
while(root):
self.stack.append(root)
root = root.left
def next(self) -> int:
cur = self.stack.pop()
node = cur.right
while(node):
self.stack.append(node)
node = node.left
return cur.val
def hasNext(self) -> bool:
return len(self.stack)>0
# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

