BF算法+RK算法+BM算法+KMP算法笔记+实现

概念

1.什么叫子串，主串，模式串？

• 如果在字符串a中查找字符串b，那么字符串a就是主串，字符串b就是模式串
• 串中任意个连续字符组成的子序列称为该串的子串，最长的子串就等于该字符串

2.什么叫字符串匹配？

• 给定主串S，判断模式串s是否是S的子串，如果是则返回模式串s的第一个字符在主串S中的位置，否则返回-1

3.什么叫单模式串匹配，多模式串匹配？

• 单模式串匹配：在一个主串中查找一个模式串
• 多模式串匹配：在一个主串中查找多个模式串

4.什么叫字符串的前缀、后缀、部分匹配值？

• 'ababa’的前缀有{a,ab,aba,abab}，后缀有{a,ba,aba,baba}，两个集合的交集为{a,aba}，其中aba为最长的相等前后缀，长度为3，所以字符串’ababa’的部分匹配值就为3
• 注意：'a’的前缀和后缀都为空集

暴力匹配算法

• BF(BruteForce)算法：暴力匹配算法(也称朴素模式匹配算法)
• 算法原理：检查主串中起始位置为1、2…n-m的子串是否跟模式串匹配
• 时间复杂度：O(nm)，最坏情况下要比对n-m+1次，每次需比对m个字符（注：笔记里所有时间复杂度中的n表示主串长度，m表示模式串长度）
• 空间复杂度：O(1)
• 特点：简单，对于不长的字符串适用
  
• c++代码实现

//字符串暴力匹配算法
int BF_Match(string masterStr, string patternStr) 
{
	//声明三个循环变量
	int i, j, k;
	//注意最坏情况下要比对n-m+1次
	for (i = 0; i < masterStr.size() - patternStr.size() + 1; i++)
	{
		//i的值代表已经比较了多少次，也同时代表主串中起始比对的字符的下标
		//j的值代表主串中起始比对的字符的下标
		//k的值代表模式串中起始比对的字符下标，模式串总是从0开始比对
		for (j = i, k = 0; k < patternStr.size(); j++, k++)
		{
			if (masterStr[j] != patternStr[k]) {
				break;//出现不匹配的字符立马终止，进入下轮匹配
			}
		}
		if (k == patternStr.size()) {
			return i;//匹配成功
		}
	}
	return -1;
}

RK算法

• Rabin-Karp算法：由两位发明者Rabin和Karp的名字命名
• 算法原理：是借助哈希算法对BF算法的改造。对主串的n-m+1个与模式串等长的子串求哈希值(哈希函数依情况而定)，然后拿每个子串的哈希值与模式串的哈希值比对，若相等则匹配
• 整个RK算法包括两部分：①求所有子串哈希值部分 ②子串哈希值与模式串哈希值比较部分
• 时间复杂度：O(n)，第①部分只需扫描一遍主串就能算出所有子串哈希值(n-m+1个)，因此为O(n)，第②部分每次哈希值比较的时间复杂度为O(1)，需比较n-m+1次
• 空间复杂度：O(1)，可以不用数组来预先存储每个子串的哈希值，算出一个值就与模式串的值比较一次，若匹配就不必算后面子串的哈希值了，所以没用额外空间
• 特点：相对BF算法而言，减少了比较的时间，但增加了计算哈希值的时间，所以哈希算法的设计很重要
• 实现(略)

BM算法

• Boyer-Moore算法

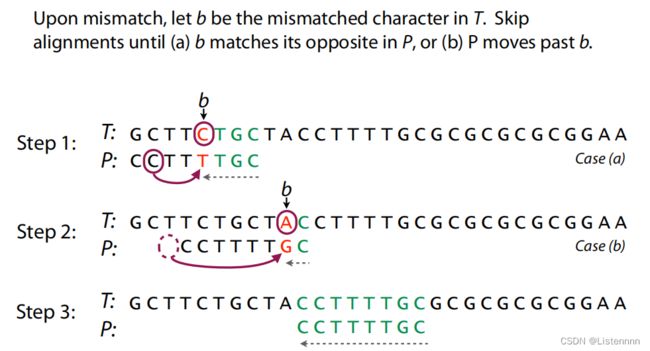
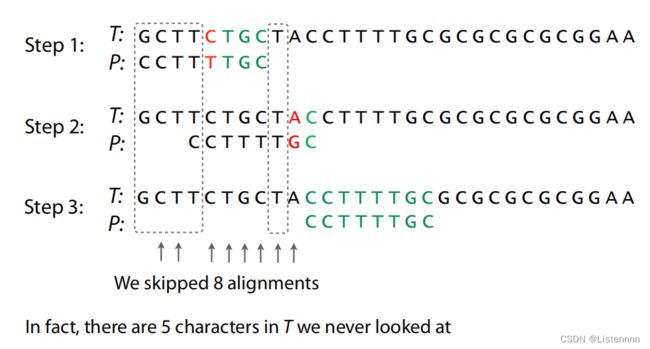
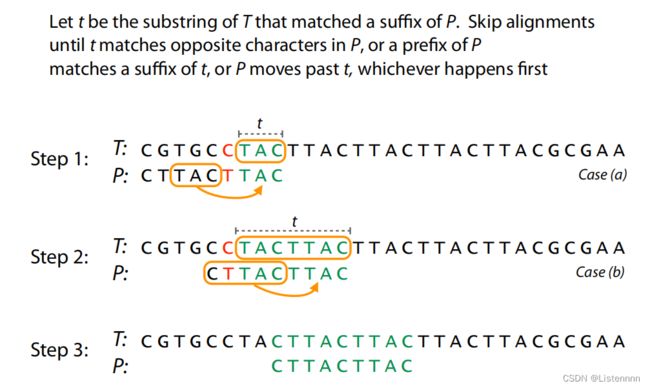
• BM算法原理包含两部分：坏字符规则、好后缀规则

• 坏字符规则示例1
  

• 坏字符规则示例2
  

• 好后缀规则示例1
  

• 好后缀规则示例2
  

• 两个规则合用示例
  

• 特点：是从后往前进行匹配，利用模式串本身的信息，去跳过一些肯定不匹配的情况。用散列表预存每个坏字符在模式串中对应的下标，也预存每个好后缀首字符在模式串中对应的下标。另外，好后缀规则可独立于坏字符规则使用。BM算法效率比KMP算法更好，但预处理更为复杂，所占内存空间更多。
  

• 时间复杂度：最坏情况O(n)，最好情况(n/m)

• 空间复杂度：O(m)

• c++代码实现

#include
#include
using namespace std;

int main() {
	string masterStr, patternStr;
	cout << "请输入主串：";
	getline(cin, masterStr);//可输入带空格的字符串
	cout << "请输入模式串：";
	getline(cin, patternStr);
	cout << BM_Match(masterStr, patternStr);
}

int BM_Match(string masterStr, string patternStr) 
{
	int indexOfBadChar[256]; //记录模式串中每个字符最后出现的下标位置
	generateHashTable(patternStr, indexOfBadChar);//构建坏字符哈希表
	int* suffix = new int[patternStr.size()];//存储在模式串中跟好后缀相匹配的子串的起始下标值
	bool* prefix = new bool[patternStr.size()];//记录模式串的后缀子串是否匹配模式串的前缀子串
	generateSuffixAndPrefix(patternStr, suffix, prefix);
	int firstMatchIndex = 0;//表示主串与模式串对齐的第一个字符，即：主串从第几个字符开始与模式串进行匹配
	while (firstMatchIndex <= masterStr.size() - patternStr.size()) 
	{
		int lastMatchIndex;//循环变量,也是模式串从后往前匹配的字符的下标
		for (lastMatchIndex = patternStr.size()-1; lastMatchIndex >= 0; lastMatchIndex--)//模式串从后往前匹配
		{
			//firstMatchIndex + lastMatchIndex是与模式串从后往前的匹配中，主串里对应字符的下标
			if (masterStr[firstMatchIndex + lastMatchIndex] != patternStr[lastMatchIndex]) break;//此时，坏字符对应的模式串中字符的下标是lastMatchIndex
		}

		//说明匹配成功，返回主串与模式串第一个匹配的字符的位置
		if (lastMatchIndex < 0) return firstMatchIndex;
		
		/*否则，将模式串往后滑动(lastMatchIndex - indexOfBadChar)位
		其中，lastMatchIndex是坏字符对应的模式串中字符的下标，indexOfBadChar是坏字符在模式串中的位置下标
		indexOfBadChar预先存在了hash表中，所以可以直接取出来*/
		int stepsByBadCharRule = lastMatchIndex - indexOfBadChar[(int)masterStr[firstMatchIndex + lastMatchIndex]];//等同于模式串往后滑动的位数
		int stepsByGoodSuffixRule = 0;
		if (lastMatchIndex < patternStr.size() - 1) //如果遇到坏字符时存在好后缀
		{
			stepsByGoodSuffixRule = moveByGoodSuffixRule(lastMatchIndex, patternStr.size(), suffix, prefix);
		}
		int steps = max(stepsByBadCharRule, stepsByGoodSuffixRule);
		firstMatchIndex = firstMatchIndex + steps;
	}
	return -1;//匹配失败
}

int moveByGoodSuffixRule(int lastMatchIndex, int sizeOfPattern, int suffix[], bool prefix[])
{
	//lastMatchIndex表示坏字符对应的模式串中字符的下标
	int k = sizeOfPattern - lastMatchIndex - 1; //k代表好后缀长度
	if (suffix[k] != -1) return lastMatchIndex - suffix[k] + 1;
	
	//lastMatchIndex是坏字符，lastMatchIndex+1是好后缀起始，lastMatchIndex+2是好后缀的后缀子串起始
	for (int suffixSub = lastMatchIndex + 2; suffixSub < sizeOfPattern; suffixSub++)
	{
		if (prefix[sizeOfPattern - suffixSub] == true) return suffixSub;
	}
	return sizeOfPattern;
}

/*
假设字符串的字符集不大，每个字符长度是1字节，用大小为256的数组来记录每个字符在模式串中出现的位置
数组下标为对应字符的ASCII码值，数组中存储这个字符在模式串中出现的位置
该哈希表记录坏字符在模式串中的位置下标，若模式串中不存在该坏字符则值为-1
*/
void generateHashTable(string patternStr, int indexOfBadChar[]) 
{
	//初始化哈希表，数组大小为256，因为ASCII码是一个字节
	for (int i = 0; i < 256; i++)
	{
		indexOfBadChar[i] = -1;
	}
	//计算模式串中每个字符的下标位置，存到哈希表中，若模式串中有相同字符，则记录位置靠后字符的下标
	for (int i = 0; i < patternStr.size(); i++)
	{
		int ascii = (int)patternStr[i];
		indexOfBadChar[ascii] = i;
	}
}

/*
suffix数组的下标表示后缀子串的长度，存储在模式串中跟好后缀相匹配的子串的起始下标值
prefix数组来记录模式串的后缀子串是否匹配模式串的前缀子串
好后缀本身就是模式串的后缀子串
好后缀规则的两个核心内容：
1.在模式串中，查找与好后缀匹配的子串
2.在好后缀字符串的后缀子串中，查找最长的能和模式串前缀子串匹配的后缀子串
*/
void generateSuffixAndPrefix(string patternStr, int suffix[], bool prefix[]) 
{
	//初始化两个数组
	//suffix[i] = -1表示模式串中不存在跟长度为i的好后缀匹配的子串
	//prefix[i] = -1表示模式串中没有跟长度为i的后缀子串匹配前缀子串
	for (int i = 0; i < patternStr.size(); i++)
	{
		suffix[i] = -1;
		prefix[i] = false;
	}
	
	for (int subStr = 0; subStr < patternStr.size(); subStr++)
	{
		//startIndex是相同后缀子串的起始下标
		int startIndex = subStr;
		//相同后缀子串的长度
		int k = 0;
		//拿下标从0到subStr的子串(subStr从0到模式串长度-2)与整个模式串求相同后缀子串
		while (startIndex >= 0 && patternStr[startIndex] == patternStr[patternStr.size() - 1 - k])
		{
			//记录suffix[k] = startIndex
			suffix[k] = startIndex;
			--startIndex;
			++k;
		}
		//如果startIndex等于0，则说明，相同后缀子串也是模式串的前缀子串，则记录prefix[k] = true
		if (startIndex == -1) prefix[k] = true;
	}
}

//算法学习中，相较于视频讲解与演示，文字显得如此无力，所以学算法最好看视频学，文字只适于总结补充，验证和梳理思路

KMP算法

• KMP 算法是根据三位作者（D.E.Knuth，J.H.Morris，V.R.Pratt）的名字来命名，全称是 Knuth Morris Pratt 算法
• 算法原理：假设模式串长度为n，依次求模式串的每个前缀子串的部分匹配值(共n-1个)，放到next数组中(从next[1]开始放，next[0]放-1)，next数组长度等于模式串长度。然后利用next数组，每当匹配失败时，可以将模式串多移动几位，且不用像暴力匹配算法那样回退指向主串的指针(主串不回溯)
• 时间复杂度：O(n+m)，求next数组O(m) + KMP匹配过程O(n)
• 空间复杂度：O(m)
• 特点：和BM算法一样，依然是利用模式串本身自带的信息来提高匹配效率，不一样的是KMP是从前往后匹配，利用部分匹配成功的前缀来减少一些不必要的比较，其主要优点是主串不回溯
• C++代码实现

#include
#include
using namespace std;

int KMP_Match(string masterStr, string patternStr);
void get_Next(string patternStr, int next[]);
void optimize_Next(string patternStr, int next[], int nextPro[]);
void get_nextPro(string patternStr, int nextPro[]);
int main() {
	string masterStr, patternStr;
	cout << "请输入主串：";
	getline(cin, masterStr);
	cout << "请输入模式串：";
	getline(cin, patternStr);
	cout << KMP_Match(masterStr, patternStr);
	return 0;
}

int KMP_Match(string masterStr, string patternStr) {
	int* next = new int[patternStr.size()];
	int* nextPro = new int[patternStr.size()];
	get_Next(patternStr, next);
	optimize_Next(patternStr,next, nextPro);
	//get_nextPro(patternStr, nextPro);
	int m_index = 0;
	int p_index = 0;
	int m_size = masterStr.size();
	int p_size = patternStr.size();
	while (m_index < m_size && p_index < p_size) {
		//p_index = -1时说明上一次匹配中，主串的第m_index个位置与模式串的第一个字符不等
		if (p_index == -1 || masterStr[m_index] == patternStr[p_index]) {
			m_index++;
			p_index++;
		}else{
			//当模式串第p_index个字符与主串失配时，跳到nextPro[p_index]的位置重新与主串当前位置进行比较
			p_index = nextPro[p_index];
		}
	}
	if (p_index == patternStr.size()) {
		return m_index - patternStr.size();
	}else {
		return -1;
	}
}


void get_Next(string patternStr, int next[]) {
	//next[i]表示下标为i之前的字符串(不包括i)所具有的最长可匹配前缀的字符个数，next[0]= -1无意义，为了方便编程实现
	next[0] = -1;
	next[1] = 0;
	int i = 0, j = 1;
	while (j < patternStr.size() - 1) {
		//
		if ( i==-1 || patternStr[i] == patternStr[j]){
			//i是最长可匹配前缀的结尾下标，所以++i后就是最长可匹配前缀的字符个数
			//若因patternStr[i] == patternStr[j]进入，则next[j+1] = next[j] + 1
			next[++j] = ++i;
		}else {
			/*
			i = next[i]的含义：找次长可匹配前缀。
			怎么找？—>次长可匹配前缀就是最长可匹配前缀的最长可匹配前缀
			如果一直找不到，就递归到i==-1，i++后即最长可匹配前缀字符个数：0
			*/
			i = next[i];
		}
	}
}

//求出next数组后，优化成nextPro数组
void optimize_Next(string patternStr, int next[],int nextPro[]) {
	nextPro[0] = -1;
	for (int i = 1; i < patternStr.size(); i++)
	{
		if (patternStr[next[i]] == patternStr[i]) {
			nextPro[i] = nextPro[next[i]];
		}
		else {
			nextPro[i] = next[i];
		}
	}
}

//直接求优化后nextPro数组
void get_nextPro(string patternStr, int nextPro[]) {
	nextPro[0] = -1;
	int i = -1, j = 0;
	while (j < patternStr.size() - 1) {
		if (i == -1 || patternStr[i] == patternStr[j]) {
			++i;
			++j;
			if (patternStr[i] == patternStr[j]) {
				nextPro[j] = nextPro[i];
			}
			else {
				nextPro[j] = i;
			}
		}
		else {
			i = nextPro[i];
		}
	}
}