算法基础16 —— 递推(铺骨牌问题 + 信奥一本通 1313 位数问题 + NOIP 2002 过河卒)

基本概念

所谓递推，是指从已知的初始条件出发，依据某种递推关系，逐次推出所要求的各中间结果及最后结果。初始条件如何得到呢？其实，初始条件要么是问题本身已经给定，要么是通过对问题的分析与化简后确定的

递推的方式

• 顺推
• 逆推

递推的特点

可用递推算法求解的题目一般有以下两个特点：

• 问题可以划分成多个状态；
• 除初始状态外，其它各个状态都可以用固定的递推关系式来表示。

递推入门 — Fibonacci数列

1、1、2、3、5、8、13… …

递归写法：

#include 

using namespace std;

int fb(int n)
{
	//printf("当前调用的是第%d层\n",n);
    if (n == 1 || n == 2) return 1;
    return fb(n - 1) + fb(n - 2);
}

int main()
{
    int n;
    cin >> n;
    cout << fb(n);
    return 0;
}

由下图中的递归搜索树，会发现存在很多重叠子问题

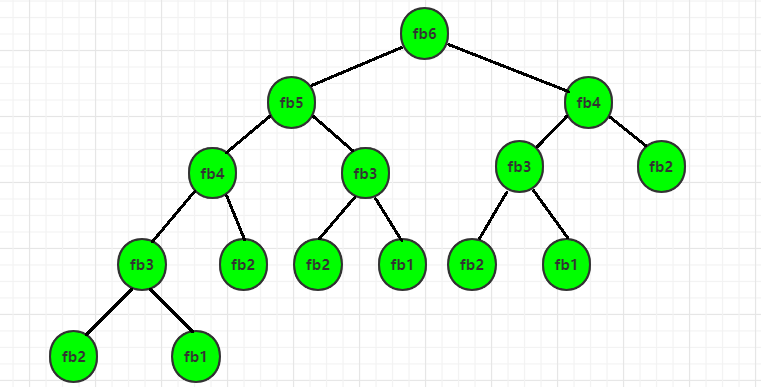
去掉注释之后，执行的结果如下：

当前调用的是第6层
当前调用的是第5层
当前调用的是第4层
当前调用的是第3层
当前调用的是第2层
当前调用的是第1层
当前调用的是第2层
当前调用的是第3层
当前调用的是第2层
当前调用的是第1层
当前调用的是第4层
当前调用的是第3层
当前调用的是第2层
当前调用的是第1层
当前调用的是第2层
8

记忆化搜索写法
将结果存储在b数组中

#include 

using namespace std;

int b[10010];//b[i]表示第i个元素的值
int fb(int n)
{
	if (b[n]) return b[n];//核心：查询b[n]是否非0,非0则直接返回本身
	//printf("当前调用的是第%d层\n",n);
    if (n == 1 || n == 2) return 1;
    b[n] =  fb(n - 2) + fb(n - 1);
    return b[n];
}

int main()
{
    int n;
    cin >> n;
    cout << fb(n);
    return 0;
}

去掉注释之后，执行的结果如下：调用层数明显减少

当前调用的是第6层
当前调用的是第4层
当前调用的是第2层
当前调用的是第3层
当前调用的是第1层
当前调用的是第2层
当前调用的是第5层
8

递推写法

#include 
using namespace std;
long long dp[55];
int main()
{
    int n;
	cin >> n;
    dp[1] = 1;
    dp[2] = 1;
    for (int i = 3;i <= 50;i++) dp[i] = dp[i - 1] + dp[i - 2];
	cout << dp[n];
	return 0;
}

---

递推 — 铺骨牌问题

有2 × n的一个长方形方格，用一个1 × 2的骨牌铺满方格。编写一个程序，试对给出的任意一个n(n>0), 输出铺法总数

算法分析

• 当n = 1时，只能是一种铺法，铺法总数有示为1
• 当n = 2时，骨牌可以两个并列竖排，也可以并列横排，再无其他方法，铺法总数表示为2
• 当n=3时，骨牌可以全部竖排，也可以认为在方格中已经有一个竖排骨牌，则需要在方格中排列两个横排骨牌（无重复方法），若已经在方格中排列两个横排骨牌，则必须在方格中排列一个竖排骨牌，再无其他排列方法，因此铺法总数表示为3
• 由此可以看出，当n = 3时的排列骨牌的方法数是n = 1和n = 2排列方法数的和

推出一般规律：
对一般的n，设Xn表示n个骨牌一共有多少种的排列方法。若第一个骨牌是竖排列放置，剩下有n - 1个骨牌需要排列，这时排列方法数为Xn-1；若第一个骨牌是横排列，整个方格至少有2个骨牌是横排列，因此剩下n - 2个骨牌需要排列，这时骨牌排列方法数为Xn-2。从第一骨牌排列方法考虑，只有这两种可能，所以有：Xn = Xn-1 + Xn-2 （n > 2）
这就是问题求解的递推公式，当n = 1和n = 1时，答案已知，故任意给定的n都可以从递推中获得解答

---

经典例题:位数问题(信奥一本通1313)

原题链接
题目描述

在所有的N位数中，有多少个数中有偶数个数字3？由于结果可能很大，你只需要输出这个答案对12345取余的值。

输入格式

读入一个数N(1<=N<=1000)

输出格式

输出有多少个数中有偶数个数字3

输入样例

2

输出样例

73

样例说明

在所有的2位数字，包含0个3的数有72个，包含2个3的数有1个，共73个

分析：
① 当N取1时，所有的一位数为0、1、2、3、4、5、6、7、8、9，其中，含偶数个3的数字为0、1、2、4、5、6、7、8、9，共9个
② 当N取2时，分两种情况。

• 若第二个数字是3，那么第一个数字必也是3(两个3)；
• 若第二个数字不是3(九种情况)，第一个数字也不是3且不能为0(八种情况)，共8 x 9 = 72种可能。

综上，当N取2时，一共有73个数字包含偶数个3
不妨设f[n][0]表示包含偶数个3的n位数的个数。
不妨设f[n][1]表示包含奇数个3的n位数的个数。

那么，如何得到n位数中包含偶数个3的方案数呢？
如下图，假设一个n位数最后一位数字是3，那么只有满足其前n - 1位包含奇数个3，才可以使n位包含偶数个3，即f[n - 1][1]

如下图，假设一个n位数最后一位数字不是3，可能取0、1、2、4、5、6、7、8、9(最后一位有9种情况)，那么只有满足其前n - 1位包含偶数个3，才可以使n位包含偶数个3，即f[n - 1][0] * 9

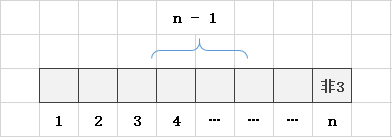
由以上分析得：

f[n][0] = f[n - 1][1] + f[n - 1][0] * 9 

同理：

f[n][1] = f[n - 1][0] + f[n - 1][1] * 9

AC代码

#include 

using namespace std;

const int N = 1010;
//f[i][0]:i位数中包含偶数个3的方案数
//f[i][1]:i位数中包含奇数个3的方案数
int f[N][2];

int main()
{
    int n;
    cin >> n;
    
    //初始化
    //f[1][0]:一位数中包含偶数个3的方案数(0 1 2 4 5 6 7 8 9)
    //f[1][1]:一位数中包含奇数个3的方案数(3)
    f[1][0] = 9;
    f[1][1] = 1;
    
    //递推
    for (int i = 2;i <= n;i++)
    {
        int num = 9;//非首位元素可以为0,有9种可能
        if (i == n) num = 8;//首位元素不能为0,有8种可能
        f[i][0] = (f[i - 1][1] + f[i - 1][0] * num) % 12345;
        f[i][1] = (f[i - 1][0] + f[i - 1][1] * num) % 12345;
    }
    
    //f[n][0]:n位数中包含偶数个3的方案数
    cout << f[n][0] << endl;
    return 0;
}

---

过河卒问题

原题链接
问题描述

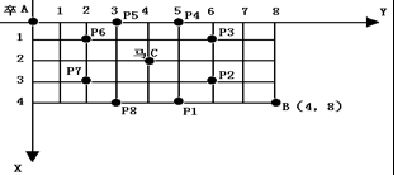
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如C点)，该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n,m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

DFS写法：

递推写法：
分析：要到达棋盘上的一个点，只能从左边过来或是从上面过来，根据加法原理，到达某一点的路径数目，就等于到达其相邻的上点和左点的路径数目之和

状态设计：用F[i][j]表示从起点到达点(i,j)的路径数目，g[i][j]表示点(i, j)有无障碍，g[i][j] = 0表示无障碍，g[i][j] = 1表示有障碍

递推关系式如下：

F[i][j] = F[i-1][j] + F[i][j-1] //i>0且j>0且g[i][j]= 0

递推边界有4个：

F[i][j] = 0 //g[i][j] = 1
F[i][0] = F[i-1][0] //i > 0且g[i][j] = 0
F[0][j] = F[0][j-1] //j > 0且g[i][j] = 0
F[0][0] = 1

考虑到最大情况下：n = 20,m = 20，路径条数可能会超过2^31-1，所以要用long long