CSP-J2019第二轮 解题分析

1.数字游戏

算法分析

共8个字符，可以用循环读入，也可以用$scanf$一次性读入。然后判断计数。

#include 
#include 
#include 
#define ll long long
using namespace std;
int main()
{
	char c;
	int num = 0;
	for (int i = 1; i <= 8; ++i)
	{
		cin>>c;
		if (c == '1') ++num;
	}
	cout<<num<<endl;
} 

2.公交换乘

算法分析

依次读入。判断是地铁的话，结果累加，然后将该地铁的信息放进队列中，队列用数组维护即可。判断是公交车的话，首先维护队首，让超出时间范围的地铁票出队，然后在队列中寻找票价大于当前的公交车票价的地铁票。使用过的地铁票要标记。每次是公交车的时候，最多在45个地铁中选，时间复杂度最坏情况下为$O(45n)$。

#include 
#include 
#include 
#define ll long long
using namespace std;
int q[100010], l = 1, r;
int vis[100010];
struct node
{
	int price, t;
}a[100010];
int main()
{
	int ans = 0;
	int n; scanf("%d", &n);
	int stype, sprice, st;
	for (int i = 1; i <= n; ++i)
	{
		scanf("%d%d%d", &stype, &sprice, &st);
		if (stype == 0)
		{
			ans += sprice;
			a[i].price = sprice; a[i].t = st;
			q[++r] = i;
		}else
		{
			while (l <= r && st - a[ q[l] ].t > 45) ++l;
			int ok = 0;
			for (int j = l; j <= r; ++j)
				if (a[ q[j] ].price >= sprice && vis[j] == 0)
				{
					vis[j] = 1;
					ok = 1;
					break;
				}
			if (!ok) ans += sprice;
		}
	}
	printf("%d\n", ans);
	return 0;
} 

算法拓展

用队列维护地铁票的信息，因为最优决策不具有单调性，所以还需要标记，有个更简便的办法，改用双向链表去维护地铁票的信息，可以做到$O(1)$删除。数组模拟双向链表。每个地铁票只会被访问一次，整体时间复杂度$O(n)$。

3.纪念品

算法分析

每天每件纪念品可以被买和卖无限次，相当于在每天的第一时刻，把所有纪念品卖掉换成钱，然后当天后面纯是买的动作。在同一天内买卖纪念品不能赚取差价，当天买第二天卖才可能赚取差价，每个纪念品可以被无限次买，即纪念品的数量是无穷的。问题转化为：

在每一天的开始，有$m$元钱，有$n$个纪念品，每个纪念品有无穷多个，第$i$个纪念品有体积为$price[i]$，即它的价格，价值为第二天的价格和当天的价格之差，可正可负。完全背包模型。

$f[i][j]：$规划到第$i$个物品，目前手里的钱有$j$元，将买来的纪念品第二天都卖掉，所能获得的最大收益。

$$f[i][j]=max(f[i-1][j],f[i][j+p[k][i]]-p[k][i]+p[k+1][i])$$

$p[k][i]$表示第$k$天第$i$个纪念品的价格。

等号左侧的$j$要小于右侧的$j+p[k][i]$，因此要逆序循环体积。$f[i][j+p[k][i]]$此时也表示是本行的状态，符合完全背包模型。

注意边界处理。$f[i][m]$表示手里有$m$元钱的最大收益，此时手里的钱没花，因此第二天也不会有收益，赋值为$m$。可将$f[0][m]=m$作为边界，以后会自动赋值。

#include
#include
#include
#include 
using namespace std;
int T, n, m, p[110][110], f[110][10010];
int main()
{
	scanf("%d%d%d", &T, &n, &m);
	for (int i = 1; i <= T; ++i) for (int j = 1; j <= n; ++j) scanf("%d", &p[i][j]);	
	// f[i][j]:规划到第i个物品，手里还剩j元钱，第二天把物品都卖掉的总收益  
	for (int k = 1; k < T; ++k)
	{
		for (int i = 0; i <= 10000; ++i) m = max(m, f[n][i]);
		memset(f, 0xcf, sizeof(f)); 
		f[0][m] = m;  // 边界  
		for (int i = 1; i <= n; ++i)
		{		
			for (int j = m; j >= 0; --j)
				if (j <= m - p[k][i]) f[i][j] = max(f[i-1][j], f[i][j + p[k][i]] - p[k][i] + p[k+1][i]);   // 取或不取 
				else f[i][j] = f[i-1][j];	// 不取  
		}
	}
	for (int i = 0; i <= 10000; ++i) m = max(m, f[n][i]);
	printf("%d\n", m);
	return 0;
}

算法拓展

1.对于买和卖这种交叉在一起的过程，就要考虑能不能过程转化。转化，是将复杂问题简单化的方式。在数据规模中提到，金币数不可能超过$10^4$，像这种字眼，就该考虑入维度了，或者$hash$思想。题面是不会给多余的信息的。

2.完全背包可以优化掉一个维度。

for (int k = 1; k < T; ++k)
{
	for (int i = 0; i <= 10000; ++i) m = max(m, f[i]);
	memset(f, 0xcf, sizeof(f)); 
	f[m] = m;  // 边界  
	for (int i = 1; i <= n; ++i)
	{		
		for (int j = m - p[k][i]; j >= 0; --j)
			f[j] = max(f[j], f[j + p[k][i]] - p[k][i] + p[k+1][i]);   // 取或不取 
			
	}
}

4.加工零件

算法分析

看描述，应知是图论模型。$n$个点$m$条边的无向非连通图。一个点完成的任务为$0$，则是需要提供原材料。查询的时候，如果$a$点和1号点不连通，结果是“No”。我们讨论下连通时的情况，$a$点要完成的任务是$L$。

假设$L=7$，$a$点距离1的距离是3，则$a$点可以通过“跳过去再跳过来”的方式消耗掉2的倍数，$a$点可以完成为3的零件。此时，可以推出1号点完成的任务为0，需要提供原材料。如果$a$点距离1的距离是4，$a$点通过以上方式消耗，可以完成为5的零件，倒推到1号点的时候，1号点可以完成为1的零件。这种情况下，也是“No”。同样可以枚举$L=6$，距离为3和4的情况。可以得出，在处理$a$点到1号点的距离时分奇偶。

如果$L$为奇数，距离为奇数且小于等于$L$，则为“Yes”，否则为“No”。如果$L$为偶数，距离为偶数且小于等于$L$，则为“Yes”，否则为“No”。

$a$点距离1号点的路径也许并非一条，尤其是有环的情况下，不同路径会更多。路径长度有奇数也会有偶数。思考发现，只需要最短奇数路径长度和最短偶数路径长度。设$dis1[i]$表示1到$i$号点的偶数最短路，$dis2[i]$表示1到$i$号点的奇数最短路。对于起点1，只存在偶数最短路，$dis1[1]=0$。其余初始化为正无穷。用dij + 堆优化、bfs或spfa都可以。现在转化为了最短路问题。

对于$u->v$，如果$dis1[u]$存在，则$dis2[v]=dis1[u]+1$。如果$dis2[u]$存在，则$dis1[v]=dis2[u]+1$。

#include
#include
#include
#include 
#include 
using namespace std;
int n, m, q, cnt, h[100010];
int dis1[100010], dis2[100010];  // dis1:偶数最短路，dis2:奇数最短路  
struct node
{
	int next, to;
}edg[200010];
queue<int> sq;
void sadd(int u, int v)
{
	++cnt;
	edg[cnt].next = h[u];
	edg[cnt].to = v;
	h[u] = cnt;
}
void spfa()
{
	dis1[1] = 0; 
	sq.push(1); 
	while (sq.size())
	{
		int u = sq.front(); sq.pop(); 
		for (int i = h[u]; i; i = edg[i].next)
		{
			int v = edg[i].to;
			if (dis1[u] != 0x3f3f3f3f)
			{
				if (dis2[v] > dis1[u] + 1)
				{
					dis2[v] = dis1[u] + 1;
					sq.push(v); 
				}
			}
			
			if (dis2[u] != 0x3f3f3f3f)
			{
				if (dis1[v] > dis2[u] + 1)
				{
					dis1[v] = dis2[u] + 1;
					sq.push(v); 
				}
			}
			
		}
	}
}
int main()
{
	scanf("%d%d%d", &n, &m, &q);
	int x, y;
	for (int i = 1; i <= m; ++i)
	{
		scanf("%d%d", &x, &y);
		sadd(x, y); sadd(y, x);
	}
	memset(dis1, 0x3f, sizeof(dis1));
	memset(dis2, 0x3f, sizeof(dis2));
	spfa();
	while (q--)
	{
		int a, l; scanf("%d%d", &a, &l);
		if (a == 1 && h[a] == 0) printf("No\n"); // a是孤立点  
		else if (dis1[a] == 0x3f3f3f3f && dis2[a] == 0x3f3f3f3f) printf("No\n");  // a和1不连通  
		else
		{
			if (l % 2) // 奇数  
			{
				if (dis2[a] <= l) printf("Yes\n"); else printf("No\n"); 
			}else
			{
				if (dis1[a] <= l) printf("Yes\n"); else printf("No\n");
			}
		}
	}
	return 0;
}

算法拓展

1.dij + 堆优化。边权可看作是1，非负，可以用迪杰斯特拉。

2.边权全都是1，可以直接用bfs搜，第一次到的点就是最短路。bfs的复杂度是$O(n)$。bfs求最短路一般适用于两种情况，边权全为1和边权只能为1或0。前者用普通队列，后者用双端队列，每次为0的时候，从队头入队，为1的时候从队尾入队。

3.分层图。分层图多用于求最短路径,但是最短路径中可以有k条边的权值为0，或者加了其他的附加条件。

分层图的构建步骤为：
（1）先将图复制k+1份。
（2）对于图中的每一条边，从u到$v_{i+1}$连边，$u_{i+1}$到v连边。

然后在整张图上跑相应图论算法。

博客学习分层图

练习题目：飞行路线

分层图有变形应用。对于本题来讲，每层之间的点不连边，第1层和第2层之间的点连边。1号点能到达的第2层的点之间一定是奇数长度，到达的第1层的点一定是偶数长度。如果到达不了，说明没有对应的奇偶长度。以下图为例：

建立分层图后为：

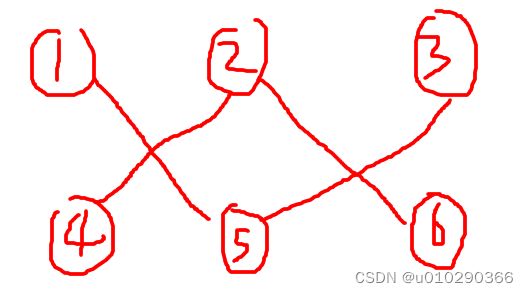
4、5、6三个点是第2层的点。1号点到不了2号点，说明1和2之间没有偶数路径。从1号点开始跑最短路即可。这里用的是dij+堆优化。

#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
struct node
{
	int next, to;
}edg[400010];
int cnt, h[200010];
void sadd(int u, int v)
{
	++cnt;
	edg[cnt].next = h[u];
	edg[cnt].to = v;
	h[u] = cnt;
}
int dis[200010], vis[200010];
queue<pair<int, int> > sq; // 大根堆  
int main()  // 分层图  
{
	int n, m, q;
	scanf("%d%d%d", &n, &m, &q);
	int u, v;
	for (int i = 1; i <= m; ++i)
	{
		scanf("%d%d", &u, &v);
		sadd(u, v + n);
		sadd(v + n, u);
		sadd(u + n, v);
		sadd(v, u + n);
	}
	memset(dis, 0x3f, sizeof(dis));

	sq.push(make_pair(0, 1));
	dis[1] = 0; 
	while (sq.size())
	{
		u = sq.front().second; sq.pop();
		if (vis[u]) continue;
		vis[u] = 1;
		for (int i = h[u]; i; i = edg[i].next)
		{
			v = edg[i].to;
			if (dis[v] > dis[u] + 1)
			{
				dis[v] = dis[u] + 1;
				sq.push(make_pair(-dis[v], v));
			}
		}
	}
	// dis[i]:1到i的偶数最短路， dis[i+n]：1到i的奇数最短路  
	int a, L;
	while (q--)
	{
		scanf("%d%d", &a, &L);
		if (L % 2) 
		{
			if (dis[a+n] <= L) printf("Yes\n"); else printf("No\n");
		}else 
		{
			if (dis[a] <= L) printf("Yes\n"); else printf("No\n");
		}
	}
	return 0;
} 

4.记忆化搜索。有人用此法得了80分。暴力算法也是应该苦练的。

博客链接

下面是别人的代码：

用rec[u][l]表示工人u加工l阶段是否需要编号为1的人提供原料
需要：rec[u][l]=1;不需要rec[u][l]=-1;不确定：rec[u][l]=0;

#include
#define r register
using namespace std;

int read(){
    int res=0,f=1;char ch;
    while(isspace(ch=getchar()));
    if(ch=='-') f=-1,ch=getchar();
    do{
        res=res*10+ch-'0';
    }while(isdigit(ch=getchar()));
    return res*f;
}

const int maxn=2e4;
int cnt,n,m,q,sure,cntmt;
int head[maxn],rec[maxn][maxn],xfkmt[maxn],yfkmt[maxn];
bool vis[maxn][maxn];

struct edge{
    int u,v,next;
}e[maxn];

inline void adde(int x,int y){
    e[++cnt].u=x;
    e[cnt].v=y;
    e[cnt].next=head[x];
    head[x]=cnt;
}

void dfs(int now,int depth){
    if(sure==1) return;
    if(rec[now][depth]==-1||vis[now][depth]) return;
    if(rec[now][depth]==1){
        sure=1;return;
    }
    if(depth==1) {
        for(r int i=head[now];i;i=e[i].next)
            if(e[i].v==1){sure=1;break;} 
        if(sure!=1) rec[now][depth]=-1; 
        return; 
    }
    for(r int i=head[now];i;i=e[i].next){
        dfs(e[i].v,depth-1);
        vis[e[i].v][depth-1]=1;

        ++cntmt;
        xfkmt[cntmt]=e[i].v;
        yfkmt[cntmt]=depth-1;
    }
}

int main(){   
    n=read(),m=read(),q=read();
    int u,v;
    for(r int i=1;i<=m;i++){
        u=read(),v=read();
        adde(u,v);
        adde(v,u); 
    }
    int l;
    for(r int k=1;k<=q;k++){
        u=read(),l=read();
        cntmt=0;sure=-1;
        dfs(u,l);   
        if(sure==1) printf("Yes\n");
        else printf("No\n");
        rec[u][l]=sure;
        for(r int i=1;i<=cntmt;i++)
            vis[xfkmt[i]][yfkmt[i]]=!vis[xfkmt[i]][yfkmt[i]];
    }

    return 0;
}