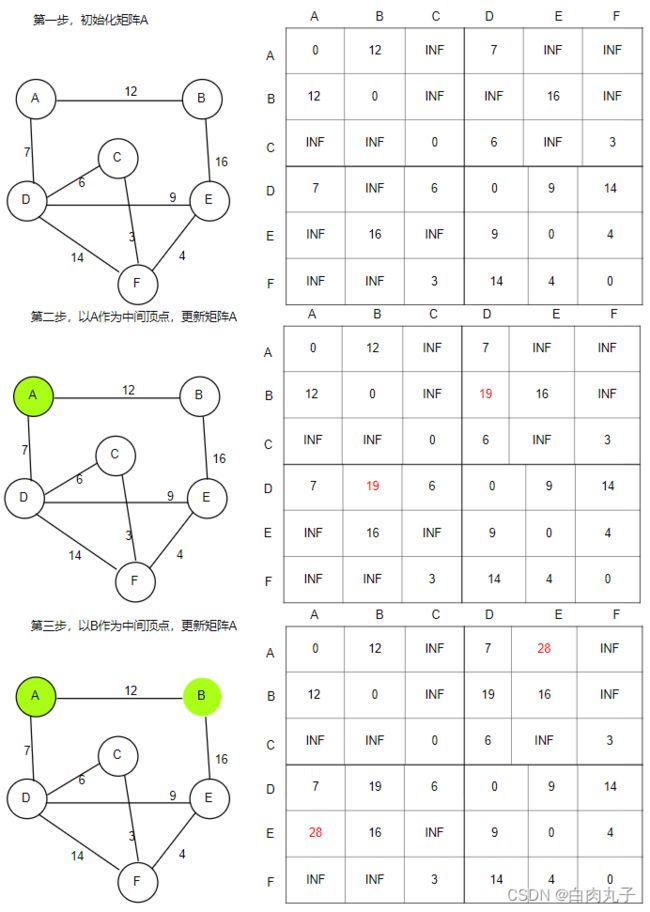
图：最短路径—Floyd算法

在了解$Floyd$算法之前，我们先了解一个函数——松弛函数。
松弛函数：对边集合$E$中任意边，以$w(u,v)$表示顶点$u$出发到顶点$v$的边的权值，以$dis[v]$表示从起点到顶点$u$的路径权值。若存在$w(u,v)$，使得$dis[v]>dis[u]+w(u,v)$，则更新$d[v]=d[u]+w(u,v)$。
松弛函数的作用就是判断是否经过某个顶点（边），可以缩短起点到终点的路径权值。

$Floyd$算法又称之为费洛伊德算法，是解决给定的有权图中顶点之间的最短路径的一种算法，允许图中有带负权值的边，但不允许有包含带负权值的边组成的回路，同时也被用于计算有向图的传递闭包。

$Floyd$算法是一种动态规划算法，对于稠密图，效率高于$Dijkstra$算法

基本思想：递推产生一个$n$阶方阵序列，其中$A^k[i][j]$表示由顶点$i$到顶点$j$的路径长度，$k$表示绕行第$k$个顶点的运算步骤，表达式描述：$$\begin{gathered} A^{-1}=arr[i][j] \\ {A}^k[i][j]=Min\{A^{k-1}[i][j],A^{k-1}[i][k]+A^{k-1}[k][j]\},k=0,1,2\dots ,n-1 \end{gathered}$$

算法步骤：

1. 初始化：方阵$A^{-1}[i][j]$表示由顶点$i$到顶点$j$的权值
2. 以顶点$A$作为中间顶点，对于每对顶点$\{i,j\}$，若$A^k[i][j]>A^k[i][k]+A^k[k][j]$，则更新$A^k[i][j]=A^k[i][k]+A^k[k][j]$。

核心代码：

for (int k = 1; k <= n; k++) 
		for (int i = 1; i <= n; i++) 
			for (int j = 1; j <= n; j++) 
				if (A[i][j] > A[i][k] + A[k][j]) {
					A[i][j] = A[i][k] + A[k][j];
					//res[i][j] = k; //记录路径
				}

由核心代码我们可以知道，$Floyd$算法的时间复杂度位$O(n^3)$；空间复杂度为$O(n^2)$