遗传算法------代码示例
目录
-
- 前言
- GA算法代码示例
-
- 1、寻找函数最大值
- 2、句子匹配
- 3、旅行商人
- 参考
前言
遗传算法就是在一个解空间上,随机的给定一组解,这组解称为父亲种群,通过这组解的交叉,变异,构建出新的解,称为下一代种群,然后在目前已有的所有解中抽取表现好的解组成新的父亲种群,然后继续上面的过程,直到达到了迭代条件或者获取到了最优解。
- 适应度
所谓的适应度,本质上可以理解为一个代价函数,或者一个规则,通过对初始种群中的个体计算适应度,能够得到对初始种群中的个体是否优劣的一个度量
- 选择
选择操作是根据种群中的个体的适应度函数值所度量的优、劣程度决定它在下一代是被淘汰还是被遗传。
- 交叉
交叉操作是将选择的两个个体p1和 p2
作为父母节点,将两者的部分码值进行交换。假设有下面的两个节点的二进制编码表示:
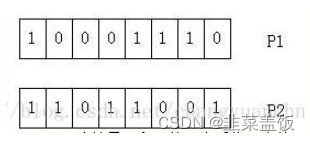
随机产生一个1到7之间的随机数,假设为3,则将p1和 p2的低三位进行互换,如下图所示,就完成了交叉操作:
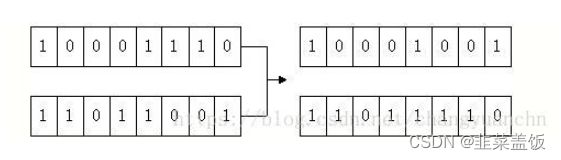
- 变异
变异操作就是改变一个DNA序列上某一个点,

我们以一定的概率进行变异的操作,例如上方的DNA序列的第6个结点,由1变成了0

GA算法代码示例
1、寻找函数最大值
首先我们生成POP_SIZE个长度为DNA_SIZE的DNA序列

pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE))
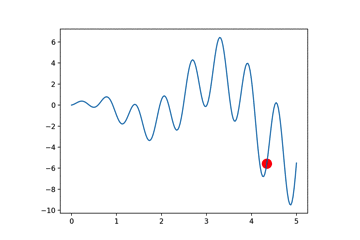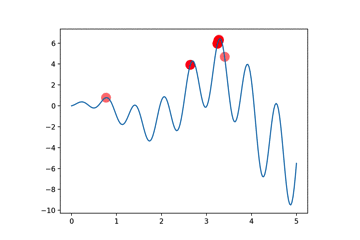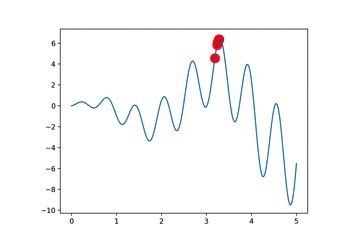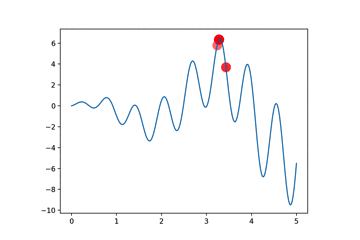
定义函数图像
def F(x):
"""
定义一个函数,就是图像中的线条
:param x:
:return:
"""
return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function
我们可以将DNA转换为函数中x轴中的某个点,将0 1 DNA序列翻译成范围在(0, 5)的数字
def translateDNA(pop):
"""
将0 1 DNA序列翻译成范围在(0, 5)的数字
:param pop:
:return:
"""
return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * X_BOUND[1]
x轴上对应的y轴上的值,我们将其称为适应度
def get_fitness(pred):
"""
获取个体的适用度
:param pred:
:return:
"""
return pred + 1e-3 - np.min(pred) #防止适应度为负数
我们从种群中选择个体
注意: 并不是每次都选择适应度最高的个体,只是适应度高的个体选择的概率比较大,其它适应度较低的个体,选择的概率小,将来适应度低的个体变异后,适应度可能会变大
def select(pop, fitness): # nature selection wrt pop's fitness
"""
从种群中选择
:param pop:
:param fitness:
:return: 所选个体的下标,可重复选择replace=True
"""
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=fitness/fitness.sum())
return pop[idx]
pop = select(pop, fitness)
之后我们对选择后的种群进行交叉和变异
def crossover(parent, pop): # mating process (genes crossover)
"""
交叉配对
:param parent:
:param pop:
:return:
"""
if np.random.rand() < CROSS_RATE:
i_ = np.random.randint(0, POP_SIZE, size=1) # select another individual from pop 从种群中选择一个个体,
cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool_) # choose crossover points 生成要交叉的位置
parent[cross_points] = pop[i_, cross_points] # mating and produce one child 进行交叉
return parent
def mutate(child):
"""
变异
:param child:
:return:
"""
for point in range(DNA_SIZE):
if np.random.rand() < MUTATION_RATE:
child[point] = 1 if child[point] == 0 else 0
return child
# 复制一个副本
pop_copy = pop.copy()
# 进行遗传 和变异
for parent in pop:
child = crossover(parent, pop_copy)
child = mutate(child)
parent[:] = child # parent is replaced by its child 父亲个体被孩子代替
最后,我们对其迭代多次
for _ in range(N_GENERATIONS):
# 得到图像上的y值
F_values = F(translateDNA(pop))
# 更新散点图
if 'sca' in globals(): sca.remove()
sca = plt.scatter(translateDNA(pop), F_values, s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.1)
# 获取每一个个体的适应度
fitness = get_fitness(F_values)
#获取最好适用度的个体下标
i = np.argmax(fitness)
print("最优DNA",pop[i,:])
pop = select(pop, fitness)
# 复制一个副本
pop_copy = pop.copy()
# 进行遗传 和变异
for parent in pop:
child = crossover(parent, pop_copy)
child = mutate(child)
parent[:] = child # parent is replaced by its child 父亲个体被孩子代替
完整代码:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import time
import numpy as np
import matplotlib.pyplot as plt
DNA_SIZE = 10 # DNA length DNA长度
POP_SIZE = 100 # population size 种群大小
CROSS_RATE = 0.8 # mating probability (DNA crossover) 交叉配对的概率
MUTATION_RATE = 0.003 # mutation probability 编译的概率
N_GENERATIONS = 200 # 代数
X_BOUND = [0, 5] # x upper and lower bounds x轴范围
def F(x):
"""
定义一个函数,就是图像中的线条
:param x:
:return:
"""
return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function
def get_fitness(pred):
"""
获取个体的适用度
:param pred:
:return:
"""
return pred + 1e-3 - np.min(pred) #防止适应度为负数
def translateDNA(pop):
"""
将0 1 DNA序列翻译成范围在(0, 5)的数字
:param pop:
:return:
"""
return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * X_BOUND[1]
def select(pop, fitness): # nature selection wrt pop's fitness
"""
从种群中选择
choice replace是true 那么适应度高的基因会被重复多选,达到进化的目的
:param pop:
:param fitness:
:return: 所选个体的下标,可重复选择replace=True
"""
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=fitness/fitness.sum())
return pop[idx]
def crossover(parent, pop): # mating process (genes crossover)
"""
交叉配对
:param parent:
:param pop:
:return:
"""
if np.random.rand() < CROSS_RATE:
i_ = np.random.randint(0, POP_SIZE, size=1) # select another individual from pop 从种群中选择一个个体,
cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool_) # choose crossover points 生成要交叉的位置
parent[cross_points] = pop[i_, cross_points] # mating and produce one child 进行交叉
return parent
def mutate(child):
"""
变异
:param child:
:return:
"""
for point in range(DNA_SIZE):
if np.random.rand() < MUTATION_RATE:
child[point] = 1 if child[point] == 0 else 0
return child
if __name__ == '__main__':
# initialize the pop DNA s生成0-1的POP_SIZE行 DNA_SIZE列的种群
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE))
plt.ion() # something about plotting
# x轴
x = np.linspace(*X_BOUND, 200)
plt.plot(x, F(x))
# 迭代N_GENERATIONS次
for _ in range(N_GENERATIONS):
# 得到图像上的y值
F_values = F(translateDNA(pop))
# 更新散点图
if 'sca' in globals(): sca.remove()
sca = plt.scatter(translateDNA(pop), F_values, s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.1)
# 获取每一个个体的适应度
fitness = get_fitness(F_values)
#获取最好适用度的个体下标
i = np.argmax(fitness)
print("最优DNA",pop[i,:])
pop = select(pop, fitness)
# 复制一个副本
pop_copy = pop.copy()
# 进行遗传 和变异
for parent in pop:
child = crossover(parent, pop_copy)
child = mutate(child)
parent[:] = child # parent is replaced by its child 父亲个体被孩子代替
plt.ioff()
plt.show()
2、句子匹配
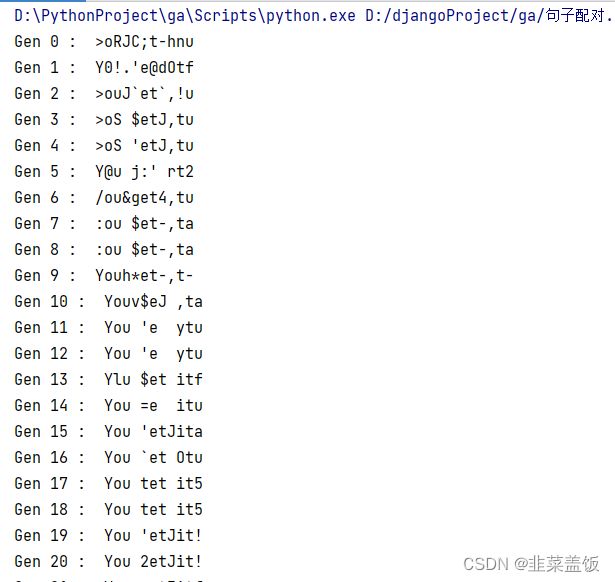
句子匹配与寻找函数最大值的区别就是DNA的表示不同,寻找函数最大值的DNA为0 1表示的,而句子匹配将字母转换为ASCII表示,多个字母组成的ASCII序列就表示为DNA
即 [ 89 111 117 32 103 101 116 32 105 116 33] 用ASCII翻译过来就是句子'You get it!'
其次 代码将进化算法封装到了一个类中
完整代码:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import numpy as np
TARGET_PHRASE = b'You get it!' # target DNA 目标句子
POP_SIZE = 300 # population size 种群大小
CROSS_RATE = 0.4 # mating probability (DNA crossover) 交叉的概率
MUTATION_RATE = 0.01 # mutation probability 变异的概率
N_GENERATIONS = 1000 # 迭代次数
DNA_SIZE = len(TARGET_PHRASE) #DNA长度(就是句子长度)
TARGET_ASCII = np.frombuffer(TARGET_PHRASE, dtype=np.uint8) # convert string to number 我们用ASCII代替句子中的字母并表示DNA [64,32,56....]
ASCII_BOUND = [32, 126] #字母范围
class GA(object):
def __init__(self, DNA_size, DNA_bound, cross_rate, mutation_rate, pop_size):
self.DNA_size = DNA_size
DNA_bound[1] += 1
self.DNA_bound = DNA_bound
self.cross_rate = cross_rate
self.mutate_rate = mutation_rate
self.pop_size = pop_size
# 随机生成pop_size行,大小为DNA_size的矩阵,即pop_size个DNA序列
self.pop = np.random.randint(*DNA_bound, size=(pop_size, DNA_size)).astype(np.int8) # int8 for convert to ASCII
def translateDNA(self, DNA):
"""
将DNA翻译成字母
:param DNA:
:return:
"""
return DNA.tobytes().decode('ascii')
def get_fitness(self):
"""
计算每一个个体的适应度
适应度:个体的DNA与TARGET_ASCII有多少个对应位置匹配的个数
:return:
"""
match_count = (self.pop == TARGET_ASCII).sum(axis=1)
return match_count
def select(self):
"""
选择个体成为新的种群
可重复选择同一个个体 replace=True
:return: 所选个体的下标
"""
fitness = self.get_fitness() + 1e-4 # 避免适应度为0,不严后面概率为0,就无法选择适应度为0的个体了
idx = np.random.choice(np.arange(self.pop_size), size=self.pop_size, replace=True, p=fitness/fitness.sum())
return self.pop[idx]
def crossover(self, parent, pop):
"""
交叉配对
:param parent:
:param pop:
:return:
"""
if np.random.rand() < self.cross_rate:
i_ = np.random.randint(0, self.pop_size, size=1) # select another individual from pop
cross_points = np.random.randint(0, 2, self.DNA_size).astype(np.bool_) # choose crossover points
parent[cross_points] = pop[i_, cross_points] # mating and produce one child
return parent
def mutate(self, child):
"""
变异
:param child:
:return:
"""
for point in range(self.DNA_size):
if np.random.rand() < self.mutate_rate:
child[point] = np.random.randint(*self.DNA_bound) # choose a random ASCII index
return child
def evolve(self):
pop = self.select()
pop_copy = pop.copy()
for parent in pop: # for every parent
child = self.crossover(parent, pop_copy)
child = self.mutate(child)
parent[:] = child
self.pop = pop
if __name__ == '__main__':
# 初始化
ga = GA(DNA_size=DNA_SIZE, DNA_bound=ASCII_BOUND, cross_rate=CROSS_RATE,
mutation_rate=MUTATION_RATE, pop_size=POP_SIZE)
# 迭代多次
for generation in range(N_GENERATIONS):
# 得到每一个个体的适应度
fitness = ga.get_fitness()
# 打印显示最好的DNA
best_DNA = ga.pop[np.argmax(fitness)]
best_phrase = ga.translateDNA(best_DNA)
print('Gen', generation, ': ', best_phrase,best_DNA)
#得到目标句子就可以结束了
if best_phrase == TARGET_PHRASE:
break
ga.evolve()
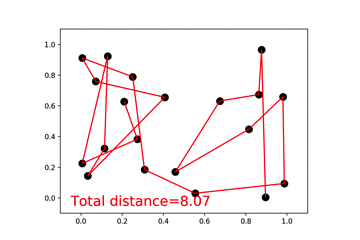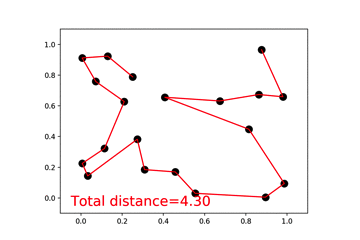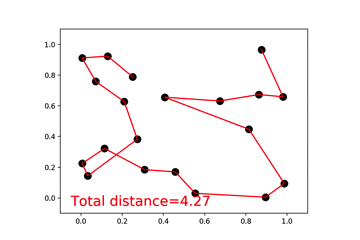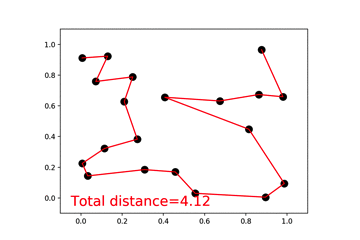
3、旅行商人
该实例目的就是画出最短的连线,
这里只说与前两个例子的不同之处
DNA的表示方法与前两个不同
我们尝试对每一个城市有一个 ID, 那经历的城市顺序就是按 ID 排序咯. 比如说商人要经过3个城市, 我们就有
0-1-2
0-2-1
1-0-2
1-2-0
2-0-1
2-1-0
这6种排列方式. 每一种排列方式我们就能把它当做一种 DNA 序列,
我们将DNA翻译成图中的x轴的点列表和y轴的点列表
DNA 是一个表示城市顺序的数组,city_position 是一个包含城市坐标的数组。
这个方法的目的是将城市坐标按照 DNA 中的顺序排列,并将 x 坐标和 y 坐标分别存储在 line_x 和 line_y 中。
DNA翻译函数如下:
def translateDNA(self, DNA, city_position): # get cities' coord in order
"""
DNA 是一个表示城市顺序的数组,city_position 是一个包含城市坐标的数组。
这个方法的目的是将城市坐标按照 DNA 中的顺序排列,并将 x 坐标和 y 坐标分别存储在 line_x 和 line_y 中。
:param DNA: 这里的DNA是pop_size个 不是一个
:param city_position:
:return:
"""
line_x = np.empty_like(DNA, dtype=np.float64) #存放x轴的点
line_y = np.empty_like(DNA, dtype=np.float64) # 存放y轴的点
for i, d in enumerate(DNA): #根据DNA中的每个城市顺序获取坐标
city_coord = city_position[d] #根据d重新排列city_position的顺序得到city_coord
line_x[i, :] = city_coord[:, 0] # 将city_coord数组的第一列的值赋给line_x数组的第 i 行
line_y[i, :] = city_coord[:, 1]
return line_x, line_y
另外我们根据路线的长度获取适应度,长度越长适应度越小
计算指数函数的值,作为适应度值。指数函数的值越大,适应度越高。指数函数的指数越小,适应度越高。
所以,适应度值与路径的总距离成反比,路径的总距离越小,适应度越高。
我们用下方的公式表示
另一方面我们可以扩大距离的适应度差
例如:长度4.5 和长度5 的适应度之差比5-4.5=0.5大
fitness = np.exp(self.DNA_size * 2 / total_distance)
获取适应度的函数如下:
def get_fitness(self, line_x, line_y):
"""
获取适应度
:param line_x:
:param line_y:
:return:
"""
total_distance = np.empty((line_x.shape[0],), dtype=np.float64) #创建一个空数组,长度line_x.shape[0]
for i, (xs, ys) in enumerate(zip(line_x, line_y)):
# 求每一个个体的总距离
total_distance[i] = np.sum(np.sqrt(np.square(np.diff(xs)) + np.square(np.diff(ys))))
# 计算了指数函数的值,作为适应度值。指数函数的值越大,适应度越高。指数函数的指数越小,适应度越高。
# 所以,适应度值与路径的总距离成反比,路径的总距离越小,适应度越高。
fitness = np.exp(self.DNA_size * 2 / total_distance)
return fitness, total_distance
其次交叉的方式也有不同
我们不能将DNA序列:[2 5 1 8 4] 变为 [ 2 4 1 8 4 ]
因为这样就少了城市5
这里的交叉策略是
先从父DNA中选取若干个城市,然后在另一个DNA选取那些未在父DNA中选取的城市
p1=[0,1,2,3] (父DNA)
p2=[3,2,1,0] (另DNA)
cp=[_,b,_,b] (选好来自父DNA的点)
c1=[1,3,_,_] (先将父DNA的点填到孩子的前面)
此时除开来自爸爸的 1, 3. 还有0, 2 两个城市, 但是0,2 的顺序就按照妈妈 DNA 的先后顺序排列. 也就是 p2=[3,2,1,0] 的 0, 2 两城市在 p2 中是先有 2, 再有 0. 所以我们就按照这个顺序补去孩子的 DNA.
c1=[1,3,2,0]
交叉函数如下:
def crossover(self, parent, pop):
"""
交叉
:param parent:
:param pop:
:return:
"""
if np.random.rand() < self.cross_rate:
# 随即从种群中选取一个个体
i_ = np.random.randint(0, self.pop_size, size=1) # select another individual from pop
# 选取交叉的点
cross_points = np.random.randint(0, 2, self.DNA_size).astype(np.bool_) # choose crossover points
# 选取了父代个体中在 cross_points 为 False 的位置上的城市编码,将其赋值给 keep_city。
keep_city = parent[~cross_points] # find the city number
# swap_city 通过布尔数组从 pop[i_] 中选取了不在 keep_city 中的城市编码。
swap_city = pop[i_, np.isin(pop[i_].ravel(), keep_city, invert=True)]
# 将 keep_city 和 swap_city 进行拼接,得到了新的子代个体的 DNA 序列,
parent[:] = np.concatenate((keep_city, swap_city))
return parent
其次变异也有不同
这里的变异是将DNA序列的两个点给交换一下
变异函数如下:
def mutate(self, child):
"""
变异
这里的变异是将DNA序列的两个点给交换一下
:param child:
:return:
"""
for point in range(self.DNA_size):
if np.random.rand() < self.mutate_rate:
swap_point = np.random.randint(0, self.DNA_size)
swapA, swapB = child[point], child[swap_point]
child[point], child[swap_point] = swapB, swapA
return child
完整代码如下:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
N_CITIES = 20 # DNA长度
CROSS_RATE = 0.1 # 交叉概率
MUTATE_RATE = 0.02 # 变异概率
POP_SIZE = 500 #种群大小
N_GENERATIONS = 500 # 迭代次数
class GA(object):
def __init__(self, DNA_size, cross_rate, mutation_rate, pop_size, ):
self.DNA_size = DNA_size
self.cross_rate = cross_rate
self.mutate_rate = mutation_rate
self.pop_size = pop_size
# 生成种群
self.pop = np.vstack([np.random.permutation(DNA_size) for _ in range(pop_size)])
def translateDNA(self, DNA, city_position): # get cities' coord in order
"""
DNA 是一个表示城市顺序的数组,city_position 是一个包含城市坐标的数组。
这个方法的目的是将城市坐标按照 DNA 中的顺序排列,并将 x 坐标和 y 坐标分别存储在 line_x 和 line_y 中。
:param DNA: 这里的DNA是pop_size个 不是一个
:param city_position:
:return:
"""
line_x = np.empty_like(DNA, dtype=np.float64) #存放x轴的点
line_y = np.empty_like(DNA, dtype=np.float64) # 存放y轴的点
for i, d in enumerate(DNA): #根据DNA中的每个城市顺序获取坐标
city_coord = city_position[d] #根据d重新排列city_position的顺序得到city_coord
line_x[i, :] = city_coord[:, 0] # 将city_coord数组的第一列的值赋给line_x数组的第 i 行
line_y[i, :] = city_coord[:, 1]
return line_x, line_y
def get_fitness(self, line_x, line_y):
"""
获取适应度
:param line_x:
:param line_y:
:return:
"""
total_distance = np.empty((line_x.shape[0],), dtype=np.float64) #创建一个空数组,长度line_x.shape[0]
for i, (xs, ys) in enumerate(zip(line_x, line_y)):
# 求每一个个体的总距离
total_distance[i] = np.sum(np.sqrt(np.square(np.diff(xs)) + np.square(np.diff(ys))))
# 计算了指数函数的值,作为适应度值。指数函数的值越大,适应度越高。指数函数的指数越小,适应度越高。
# 所以,适应度值与路径的总距离成反比,路径的总距离越小,适应度越高。
fitness = np.exp(self.DNA_size * 2 / total_distance)
return fitness, total_distance
def select(self, fitness):
"""
在种群中选取个体,重新组成一个种群,
适应度大的,选取的概率就大
可重复选择,达到进化的目的 replace=True,
:param fitness:
:return: 返回一个心中群
"""
idx = np.random.choice(np.arange(self.pop_size), size=self.pop_size, replace=True, p=fitness / fitness.sum())
return self.pop[idx]
def crossover(self, parent, pop):
"""
交叉
:param parent:
:param pop:
:return:
"""
if np.random.rand() < self.cross_rate:
# 随即从种群中选取一个个体
i_ = np.random.randint(0, self.pop_size, size=1) # select another individual from pop
# 选取交叉的点
cross_points = np.random.randint(0, 2, self.DNA_size).astype(np.bool_) # choose crossover points
# 选取了父代个体中在 cross_points 为 False 的位置上的城市编码,将其赋值给 keep_city。
keep_city = parent[~cross_points] # find the city number
# swap_city 通过布尔数组从 pop[i_] 中选取了不在 keep_city 中的城市编码。
swap_city = pop[i_, np.isin(pop[i_].ravel(), keep_city, invert=True)]
# 将 keep_city 和 swap_city 进行拼接,得到了新的子代个体的 DNA 序列,
parent[:] = np.concatenate((keep_city, swap_city))
return parent
def mutate(self, child):
"""
变异
这里的变异是将DNA序列的两个点给交换一下
:param child:
:return:
"""
for point in range(self.DNA_size):
if np.random.rand() < self.mutate_rate:
swap_point = np.random.randint(0, self.DNA_size)
swapA, swapB = child[point], child[swap_point]
child[point], child[swap_point] = swapB, swapA
return child
def evolve(self, fitness):
"""
开始进化算法
:param fitness:
:return:
"""
pop = self.select(fitness)
pop_copy = pop.copy()
for parent in pop: # for every parent
child = self.crossover(parent, pop_copy)
child = self.mutate(child)
parent[:] = child
self.pop = pop
class TravelSalesPerson(object):
"""
环境
"""
def __init__(self, n_cities):
self.city_position = np.random.rand(n_cities, 2)
plt.ion()
def plotting(self, lx, ly, total_d):
plt.cla()
plt.scatter(self.city_position[:, 0].T, self.city_position[:, 1].T, s=100, c='k')
plt.plot(lx.T, ly.T, 'r-')
plt.text(-0.05, -0.05, "Total distance=%.2f" % total_d, fontdict={'size': 20, 'color': 'red'})
plt.xlim((-0.1, 1.1))
plt.ylim((-0.1, 1.1))
plt.pause(0.01)
if __name__ == '__main__':
ga = GA(DNA_size=N_CITIES, cross_rate=CROSS_RATE, mutation_rate=MUTATE_RATE, pop_size=POP_SIZE)
# 初始化环境
env = TravelSalesPerson(N_CITIES)
# 开始迭代
for generation in range(N_GENERATIONS):
lx, ly = ga.translateDNA(ga.pop, env.city_position)
fitness, total_distance = ga.get_fitness(lx, ly)
# 核心
ga.evolve(fitness)
best_idx = np.argmax(fitness)
print('Gen:', generation, '| best fit: %.2f' % fitness[best_idx], )
env.plotting(lx[best_idx], ly[best_idx], total_distance[best_idx])
plt.ioff()
plt.show()
参考
莫烦Python
遗传算法与进化算法