哈夫曼树哈夫曼编码必知必会知识

 目录

前言

哈夫曼树

1.相关背景

2.基本概念

3.什么是哈夫曼树

 3.特点

4.哈夫曼树的构造（哈夫曼算法）

5.带权路径长度计算

哈夫曼编码（哈夫曼树的应用）

1.基本概念

 2.编码方式

 3.编码依据

4.小试牛刀（习题）

---

前言

        今天我们学习一种新的数据结构----哈夫曼树，，其最大的应用就是哈夫曼编码了，下面我会详细介绍和讲解关于哈夫曼树和哈夫曼编码的相关知识点，废话不多说了，开始今天的学习吧！

哈夫曼树

1.相关背景

        1951年，哈夫曼在麻省理工学院（MIT）攻读博士学位，他和修读信息论课程的同学得选择是完成学期报告还是期末考试。导师罗伯特·法诺（Robert Fano）出的学期报告题目是：查找最有效的二进制编码。由于无法证明哪个已有编码是最有效的，哈夫曼放弃对已有编码的研究，转向新的探索，最终发现了基于有序频率二叉树编码的想法，并很快证明了这个方法是最有效的。哈夫曼使用自底向上的方法构建二叉树，避免了次优算法香农-范诺编码（Shannon–Fano coding）的最大弊端──自顶向下构建树。

1952年，于论文《一种构建极小多余编码的方法》（A Method for the Construction of Minimum-Redundancy Codes）中发表了这个编码方法。

2.基本概念

权（weight）：给树的节点赋予具有某种含义的数值，这个值表示这个节点的权重

路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径

树的路径长度：从树根到每一个结点的路径长度之和，记作：L

树的带权路径长度：树中所有叶子结点的带权路径长度之和，记作:WPL(Weighted Path Length)

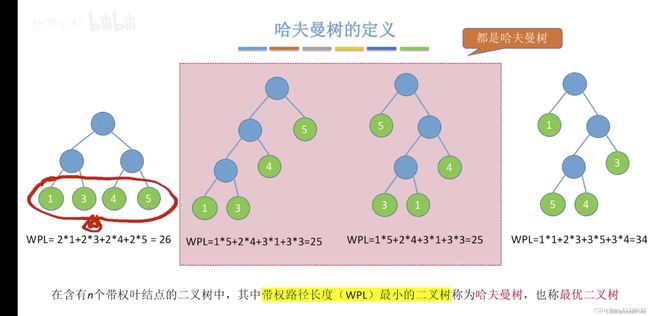
3.什么是哈夫曼树

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

哈夫曼树：最优二叉树 

 3.特点

１.满二叉树不一定是哈夫曼树

２.哈夫曼树中权越大的叶子离根越近

３.具有相同带权结点的哈夫曼树不惟一

4.带权路径长度（WPL）最短

4.哈夫曼树的构造（哈夫曼算法）

构造过程如下：

1、给定n个权值为{W1,W2,W3……Wn}的节点，构造n棵只有一个叶子节点的二叉树，从而得到一个二叉树集合F={T1,T2,T3……Tn}

2、在F中选取根结点权值最小和依次最小的两个二叉树作为左右子树，构造为一个新的二叉树，这个二叉树的根节点就是左右子树根节点权值之和

3、在集合F中删除作为左右子树的二叉树，并且把刚刚新建立的二叉树放入到集合F中去

4、重复2、3步骤，当F中只剩下一棵二叉树的时候，这个二叉树就是要建立的哈夫曼树，创建完成。

演示过程如下：

给定当前n个权值的节点，如图所示：

视频演示

 视频相关链接：哈夫曼树和哈夫曼编码_哔哩哔哩_bilibili

创建一个哈夫曼树我们会发现，如果有n个节点的话，那么创建之后的总节点为2n-1个 

5.带权路径长度计算

那么怎么去计算哈夫曼树带权路径长度呢？很简单，比如要计算某一个节点的带权路径长度，只需要把这个节点的权值w，乘上距离根结点的边数s，得到的w*s就是其带权路径长度，然后计算出每一个节点的带权路径长度，加起来即可。图示如下：

哈夫曼编码（哈夫曼树的应用）

1.基本概念

        编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。

霍夫曼编码使用一种特别的方法为信号源中的每个符号设定二进制码。出现频率更大的符号将获得更短的比特，出现频率更小的符号将被分配更长的比特，以此来提高数据压缩率，提高传输效率

 2.编码方式

1.先统计出字符集出现的权重（比例）

2.然后通过这些字符集的权重创建一个哈夫曼树，权重大的离跟节点越近

3.最后去对每一个分支进行哈夫曼编码

• 结点的左分支标0，右分支标1

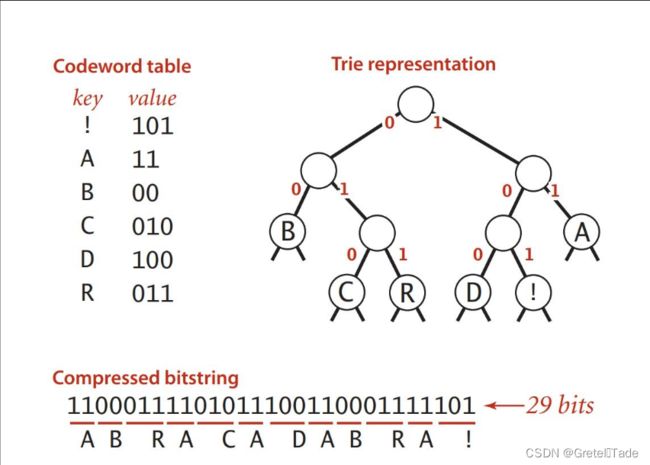
• 把从根到每个叶子的路径上的标号连接起来，作为该叶子代表的字符的编码。

图示如下：

 3.编码依据

哈夫曼编码有一个要求，就是一个节点的编码不可以是其他节点编码的前缀，目的是要保证编码的唯一性，给个示例：

        A:00        B:01        C:0000        D:101

如果电文为  AABD

那么其编码应该是：000001101

但是实际上跟电文 CBD（其编码也是000001101）有冲突，原因是，A编码是C编码的前缀

 哈夫曼树可以完美的避开这个问题，哈夫曼树的全部节点都是作叶子节点，所以没有一片树叶是其他树叶的父节点。

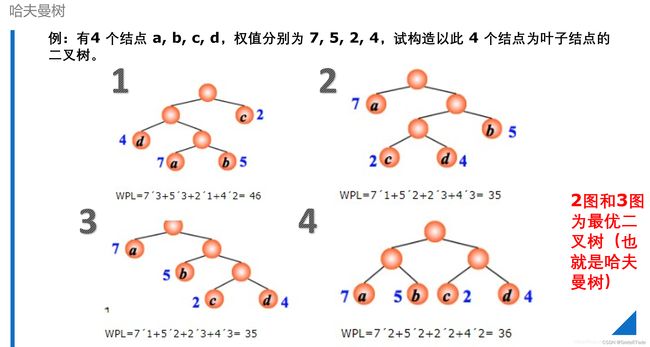
4.小试牛刀（习题）

已知字符集{ a, b, c, d, e, f }，若各字符出现的次数分别为{ 6, 3, 8, 2, 10, 4 }，则对应字符集中各字符的哈夫曼编码可能是：

A. 00, 1011, 01, 1010, 11, 100

B. 00, 100, 110, 000, 0010, 01

C. 10, 1011, 11, 0011, 00, 010

D. 0011, 10, 11, 0010, 01, 000

答案：A

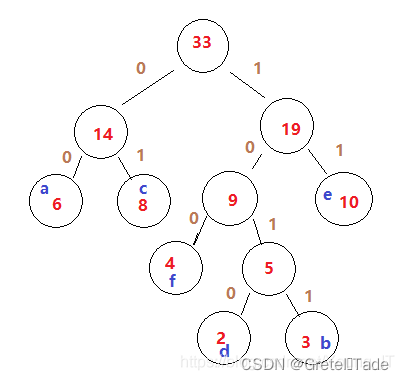
解析：根据节点构造出哈夫曼树，然后把节点标注上去，图示如下，然后按照哈夫曼编码的特点直接去读出来即可。 

 以上就是本期的全部内容了，我们下一期再见！

分享一张壁纸：