二叉树题目：二叉树寻路

题目

标题和出处

标题：二叉树寻路

出处：1104. 二叉树寻路

难度

5 级

题目描述

要求

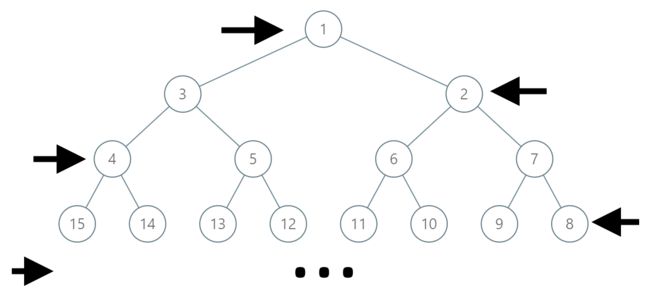
在一个无限的二叉树上，每个结点都有两个子结点，结点按行标号。

在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序标号。在偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序标号。

给定树上某一个结点的标号 $\text{label}$，返回从根结点到标号为 $\text{label}$ 的结点的路径，该路径是由途经的结点标号所组成的。

示例

示例 1：

输入：$\text{label = 14}$
输出：$\text{[1,3,4,14]}$

示例 2：

输入：$\text{label = 26}$
输出：$\text{[1,2,6,10,26]}$

数据范围

• $\text{1}\le \text{label}\le {\text{10}}^{\text{6}}$

解法

思路和算法

首先考虑一个简单的问题：如果二叉树的每一行都是按从左到右的顺序标号，如何得到从根结点到标号为 $\text{label}$ 的结点的路径。当每一行都按从左到右的顺序标号时，对于标号为 $x$ 的结点，其左子结点标号为 $2x$，右子结点标号为 $2x+1$，如果 $x>1$，则其父结点标号为 $\lfloor \frac{x}{2}\rfloor$。因此，对于给定的标号 $\text{label}$，可以利用上述性质得到从该标号结点到根结点的路径，将路径翻转之后即可得到从根结点到该标号结点的路径。

这道题中，二叉树的奇数行按从左到右的顺序标号，二叉树的偶数行按从右到左的顺序标号，因此需要将标号转换之后才能得到结点位置。考虑二叉树的每一行都是按从左到右的顺序标号，将这样的标号称为下标，和题中定义的标号区分。结点的标号与下标之间的关系如下。

• 奇数行结点的标号与下标相同。

• 偶数行结点的标号与下标不同，将整行的下标翻转之后即为标号。

这道题规定根结点在第 $1$ 层，则第 $i$ 层有 $2^{i-1}$ 个结点，结点的标号范围是 $[2^{i-1},2^i-1]$。当 $i$ 是偶数时，第 $i$ 行的每个结点的标号与下标之和为 $2^{i-1}+2^i-1$，由此可以得到同一个结点的标号与下标之间的换算关系。

根据层数与结点标号范围的关系可以定位到标号为 $\text{label}$ 的结点所在层，然后计算从标号为 $\text{label}$ 的结点到根结点的路径，最后将路径翻转即可得到从根结点到标号为 $\text{label}$ 的结点的路径。

对于标号为 $\text{label}$ 的结点，如果其所在层是奇数，则结点下标与标号相同，如果其所在层是偶数，则需要根据换算关系得到结点下标。

得到标号为 $\text{label}$ 的结点的下标之后，即可得到路径上的所有结点下标。对于每个结点下标，根据结点所在层的奇偶性和层数计算结点标号，将标号添加到路径中，当到达标号为 $1$ 的结点即根结点时，得到反向路径，将反向路径翻转即可得到结果路径。

以下用题目中的两个例子说明。

示例 1，$\text{label}=14$。标号为 $\text{label}$ 的结点在第 $4$ 层，层数是偶数，该结点的下标是 $9$。从该结点到根结点的路径上的结点的下标依次是 $[9,4,2,1]$，标号依次是 $[14,4,3,1]$，翻转后得到从根结点到标号为 $\text{label}$ 的结点的路径 $[1,3,4,14]$。

示例 2，$\text{label}=26$。标号为 $\text{label}$ 的结点在第 $5$ 层，层数是奇数，该结点的下标是 $26$。从该结点到根结点的路径上的结点的下标依次是 $[26,13,6,3,1]$，标号依次是 $[26,10,6,2,1]$，翻转后得到从根结点到标号为 $\text{label}$ 的结点的路径 $[1,2,6,10,26]$。

代码

class Solution {
    public List<Integer> pathInZigZagTree(int label) {
        int level = 1;
        int start = 1, end = 1;
        while (end < label) {
            level++;
            start *= 2;
            end = end * 2 + 1;
        }
        int num = level % 2 == 1 ? label : start + end - label;
        List<Integer> path = new ArrayList<Integer>();
        while (num > 0) {
            int curr = level % 2 == 1 ? num : start + end - num;
            path.add(curr);
            num /= 2;
            level--;
            start /= 2;
            end /= 2;
        }
        Collections.reverse(path);
        return path;
    }
}

复杂度分析

• 时间复杂度：$O(\log \text{label})$。定位到标号为 $\text{label}$ 的结点所在的层需要 $O(\log \text{label})$ 的时间，得到从根结点到标号为 $\text{label}$ 的结点的路径也需要 $O(\log \text{label})$ 的时间。

• 空间复杂度：$O(1)$。除了返回值以外，使用的空间是常数。