二叉树——从前序与中序遍历序列构造二叉树

基础首先要掌握二叉树的前序、中序、后续遍历，理解递归在二叉树操作中的重要地位，熟悉分治法在解决实际问题中的广泛应用。

题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列

作者：力扣 (LeetCode)
链接：https://leetcode-cn.com/leetbook/read/data-structure-binary-tree/xoei3r/
来源：力扣（LeetCode）

题目理解

给定一个二叉树，

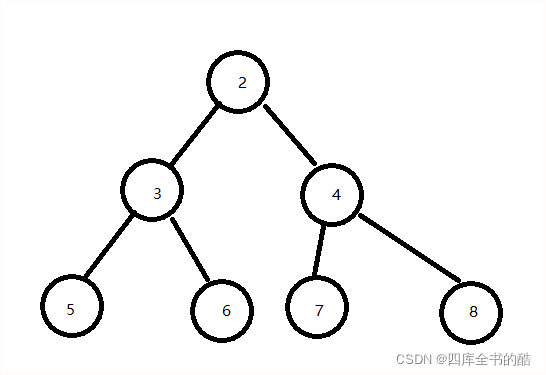
前序遍历是

[2,3,5,6,4,7,8]

中序遍历是

[5,3,6,2,7,4,8]

后序遍历是

[5,6,3,7,8,4,2]

首先，我们根据遍历的规则可以知道：
1、中序遍历的某个数字的左边全都在他的左子树，且左子树的数据在后序遍历中仍旧处于相同长度的连续区域中；右边全在他的右子树且右子树的数据在后序遍历中仍旧处于相同长度的连续区域中；
2、一个树的前序遍历的第一个是根节点；

important:
preorder:前序遍历数组；head1:前序遍历选取区间起始值下标；tail1:前序遍历选取区间结束值下标；
inorder:中序遍历数组；head2:中序遍历选取区间起始值下标；tail2:中序遍历选取区间结束值下标；

我们定义一个函数func，他的作用是：建立区间元素（中序遍历和前序遍历两个区间）所代表的树。
1、特判：结束递归的条件是选取区间不合理（即区间起始值head大于结束值tail）（两个区间head和tail是差值和大小关系一样的），返回一个NULL；或区间中只含一个元素，那它即使树的根节点，也是叶子节点，此时返回节点值为该区间元素的值的节点即可结束递归；
2、根据中序遍历获得根节点 preorder[head1] 的值 nodeval；
3、求该树的左子树和右子树；
（对区间选取的变化！！depend on nodeval）。
在中序遍历中找到val的位置下标 idx，根据规则得到；

• 左子树中序遍历起始值：head1；中序遍历结束值：idx - 1; 后序遍历起始值：head2+1；后序遍历结束值：idx；
• 右子树中序遍历起始值：idx + 1;中序遍历结束值：tail1;后序遍历起始值：idx+1;后序遍历结束值：tail2;
  (前遍历区间选择记住规则一描述的）

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.empty()) return nullptr;
        pre = preorder;
        in = inorder;
        return func(0,preorder.size() - 1,0,inorder.size() - 1);
    }
private:
    vector<int> pre,in;
    TreeNode* func(int head1,int tail1,int head2,int tail2){
        if(head1 > tail1) return nullptr;
        int nodeval = pre[head1];
        TreeNode* root = new TreeNode(nodeval);
        if(head1 == tail1) return root;

        int offset = 0;
        while(in[head2 + offset] != nodeval) offset++;
        root->left = func(head1 + 1,head1 + offset,head2,head2 + offset - 1);
        root->right = func(head1 +offset + 1,tail1,head2+offset+1,tail2);
        return root;
    }
};

总结

一定要理解遍历规则，这里的重点是
1、能意识到中序遍历根节点的左子树都在左边，右边一样；
2、前序遍历的区间是怎样选的，（规则一！规则一！规则一！！！）