粒子群算法及C++实现
参考博客
https://www.cnblogs.com/alan666/p/8311804.html
https://blog.csdn.net/weixin_39059031/article/details/103723843
https://blog.csdn.net/weixin_40679412/article/details/80571854
https://blog.csdn.net/daaikuaichuan/article/details/81382794
https://blog.csdn.net/luotuo44/article/details/33690179
https://www.cnblogs.com/esCharacter/p/9564660.html
https://blog.csdn.net/weixin_39059031/article/details/103723843
一、原理
1. 鸟群捕食行为
一个鸟群在某区域寻找食物,且这一区域仅有一份食物。鸟群不知道这份食物在哪里,但知道食物距离他们多远以及同伴的位置。鸟群怎样尽快找到食物?搜索目前离食物最近的鸟所在区域,并向这片区域靠拢。
把食物所在位置当做最优点,鸟离食物的距离作为函数适应度,则可以把鸟群寻找食物的过程看做函数寻优的过程。由此受到启发,提出了粒子群算法。
2. 粒子群算法
粒子群算法,又称粒子群优化算法(Partical Swarm Optimization),是近年发展起来的一种新的进化算法(Evolutionary Algorithm - EA),由Eberhart 博士和kennedy 博士于1995年提出,其源于对鸟群捕食的行为研究。 这种算法模拟了人类的社会行为。个体在学习自身经验的同时相互交换信息,由此,种群成员可以逐渐移到问题空间中较好的区域。
2.1 抽象
- 粒子:把每只鸟抽象成一个无质量无体积的微粒,优化寻找最优解的过程相当于鸟群寻找食物的过程。
- 速度:粒子在问题的搜索空间中以一定的速度飞行,这个速度决定它的飞行方向和距离,速度根据粒子本身的飞行经验和同伴的飞行经验来动态调整。
- 适应值:粒子需要一个由目标函数所确定的适应值,来评价粒子的“好坏”程度。 PSO算法先将一群粒子初始化(位置随机),然后通过迭代寻找最优解。每次迭代中,粒子通过跟踪两个“极值”来更新自身位置。这两个极值一个是粒子本身找到的最优解,称为个体极值pBest,另一个是整个种群目前找到的最优解,称为全局极值gBest。
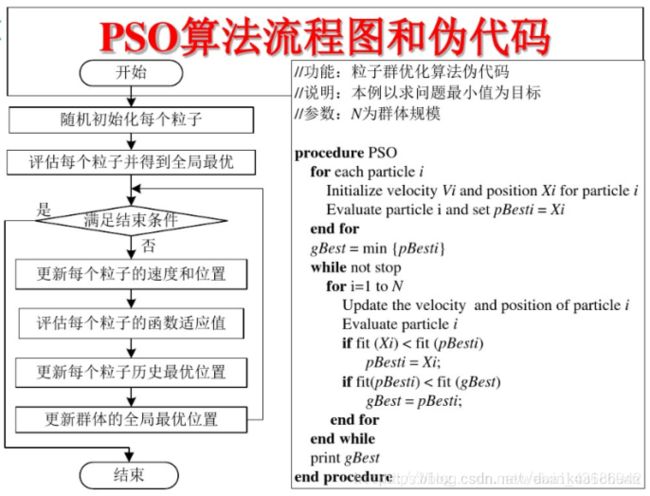
2.2 算法流程
- 初始化每个粒子群:群体规模N,每个粒子的位置xi 和速度Vi 。
- 计算每个粒子的适应度值F[i]。
- 对每个粒子,用它的适应度值F[i] 和个体极值Pbest(i) 比较,如果F[i] > Pbest(i),则用F[i]替换Pbest(i)。
- 对每个粒子,用它的适应度值F[i] 和全局极值gbest(i) 比较,如果F[i] > gbest(i),则用F[i]替换gbest(i)。
- 根据公式 2.3 中公式更新粒子位置x与速度Vi 。如果满足结束条件(误差达到要求或达到最大循环次数)则退出,否则返回步骤 2。
2.3 相关公式
将粒子延伸到N维空间,则N维空间中粒子的位置、飞行速度为矢量,粒子根据如下公式更新速度与位置:

其中w是惯性权重(加权系数),代表粒子上一轮速度对本轮的影响程度;
c1和c2是学习因子(加速度系数),代表粒子向自身最优(自我总结)和群体最优学习的能力。
rand()为0~1的随机数。
2.4 参数设置
- 粒子数量:一般取1~40. 其实对于大部分的问题10个粒子已经足够可以取得好的结果;
- 粒子的维度:由优化问题决定,如本次实验为二元函数的优化问题,所以维度为2;
- 粒子的范围::即粒子的移动区间范围,由优化问题决定,每一维可以设定不同的范围;
- W:一般取值在0.1~0.9之间,对优化影响较大,w取值较大时,有利于跳出局部最优点,w取值较小时有利于算法收敛;
- 学习因子:通常设c1 = c2 = 2,范围为0~4;
- 粒子的速度:表示粒子在一次迭代中可移动的最大距离,通常根据函数自变量取值范围来设定,例如x 属于 [-10, 10], 那么 Vmax 的大小就是 20;
二、例子
1. 题目
2. 关键代码
2.1 数据结构
本次实验数据结构设置较为简单,粒子的位置、速度和最优位置均设置为二维数组,行为粒子数量,列为函数维度。除此之外粒子群对应的适应度设为一维数组,粒子群整体最优位置设为长度为维度的数组,具体代码片如下:
double P[N][dim]; //粒子位置
double V[N][dim]; //粒子速度
double fitness[N]; //粒子适应度
double pbest[N][dim]; //粒子最优位置
double gbest[dim]; //粒子群最优位置
2.2 粒子速度与位置的更新
使用2.3中公式对粒子位置与状态进行更新。本次实验中粒子维度为2,所以需要对每个粒子的位置与速度的两个分量分别进行更新。然后更新粒子适应值,若新的适应值大于粒子的个体最优位置,则更新粒子的个体最优位置,最后再比较是否获得更优的群体最优位置,若更优则更新群体最优位置,具体代码片如下:
for (int i = 0; i < N; i++)
{
for (int j = 0; j < dim; j++)
{
//更新速度
V[i][j] = w * V[i][j] + rand(e) * (pbest[i][j] - P[i][j])
+ rand(e) * (gbest[j] - P[i][j]);
if (V[i][j] < vmin)
V[i][j] = vmin;
if (V[i][j] > vmax)
V[i][j] = vmax;
//更新位置
P[i][j] = P[i][j] + V[i][j];
if (P[i][j] < pmin)
P[i][j] = pmin;
if (P[i][j] > pmax)
P[i][j] = pmax;
}
fitness[i] = func(P[i]); //更新适应度
//更新个体最优
if (fitness[i] > func(pbest[i]))
{
pbest[i][0] = P[i][0];
pbest[i][1] = P[i][1];
}
}
//更新整体最优
index = getGbestIndex(fitness);
if (func(P[index]) > func(gbest))
{
gbest[0] = P[index][0];
gbest[1] = P[index][1];
gbestGen = g + 1;
}
2.3 随机数生成(新接触)
C++11 : default_random_engine
是C++11提供了新的随机数生成器,随机数引擎default_random_engine,使用时包含头文件#include<random>;默认情况下,default_random_engine的生成范围是一个unsigned,可以通过方法min()和max()获取生成范围;与rand()类似,default_random_engine也需要通过随机数种子改变生成的序列,设置方法可以通过调用方法seed();随机数引擎可以通过分布对象设置生成范围,uniform_int_distribution<unsigned>或uniform_real_distribution<double>;相对rand(),可以使用uniform_real_distribution<>生成随机浮点数,并且不用担心精度问题,使用方法如下:
default_random_engine e;//定义随机数引擎
uniform_int_distribution<unsigned> id(1, 10);//整型分布
uniform_real_distribution<double> dd(0, 1.0);//浮点型分布
e.seed(10);//设置随机数种子
for (size_t i = 0; i < 10; i++)
{
cout << id(e) << " ; " << dd(e) << endl;
}
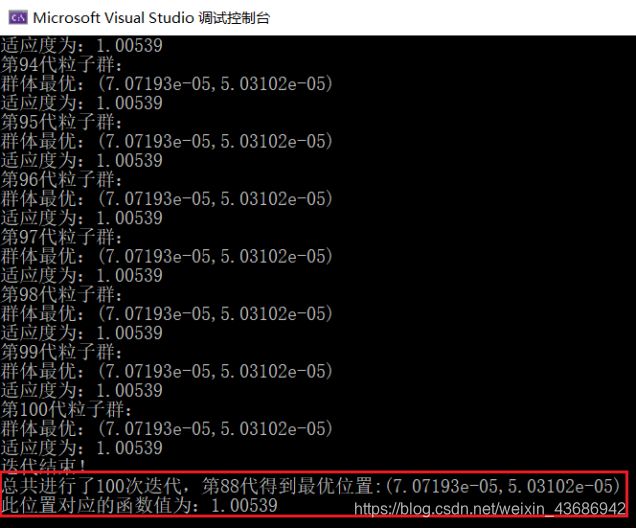
3. 结果
-
分析
在代码实现的具体过程中,遇到的问题主要是参数设置的问题。其中粒子速度与位置范围的设定一直不合适,导致粒子群在第二轮迭代时,大多数粒子会超过设定的边界,虽然将超出边界的粒子速度与位置设为边界值,但因为是大数粒子越界,所以后面的迭代也就没有了意义。通过在网络上查询相关博客,得到的解决办法是粒子速度与位置边界设定与函数的自变量和值域相关,经过分析,大概得出本次实验要优化的函数,在(0,0)位置时取得最优解,所以将粒子速度范围设为(-0.5,0.5),最终得到了较好的效果,不会再出现大量粒子越界的情况。
回想此次实验,应该还是不对,如果提前知道收敛点大概在哪,再设置参数,算法还有意义吗?
4. 源代码
#include