前端常见算法题(动态规划篇)
路径问题
2021.05.13
No.514 自由之路
电子游戏“辐射4”中,任务“通向自由”要求玩家到达名为“Freedom Trail Ring”的金属表盘,并使用表盘拼写特定关键词才能开门。
给定一个字符串 ring,表示刻在外环上的编码;给定另一个字符串 key,表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。
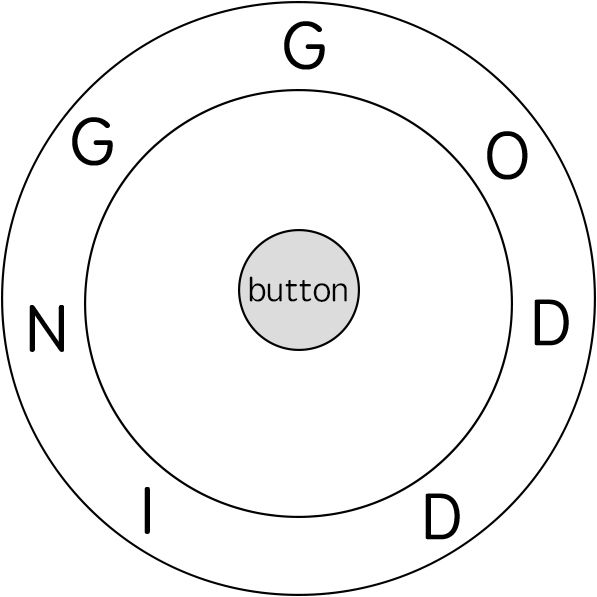
最初,ring 的第一个字符与12:00方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐,然后按下中心按钮,以此逐个拼写完 key 中的所有字符。
旋转 ring 拼出 key 字符 key[i] 的阶段中:
您可以将 ring 顺时针或逆时针旋转一个位置,计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐,并且这个字符必须等于字符 key[i] 。
如果字符 key[i] 已经对齐到12:00方向,您需要按下中心按钮进行拼写,这也将算作 1 步。按完之后,您可以开始拼写 key 的下一个字符(下一阶段), 直至完成所有拼写。
示例:
输入: ring = “godding”, key = “gd”
输出: 4
解释:
对于 key 的第一个字符 ‘g’,已经在正确的位置, 我们只需要1步来拼写这个字符。
对于 key 的第二个字符 ‘d’,我们需要逆时针旋转 ring “godding” 2步使它变成 “ddinggo”。
当然, 我们还需要1步进行拼写。
因此最终的输出是 4。
提示:
ring 和 key 的字符串长度取值范围均为 1 至 100;
两个字符串中都只有小写字符,并且均可能存在重复字符;
字符串 key 一定可以由字符串 ring 旋转拼出。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/freedom-trail
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=514 lang=javascript
*
* [514] 自由之路
*/
// @lc code=start
/**
* @param {string} ring
* @param {string} key
* @return {number}
*/
var findRotateSteps = function(ring, key) {
// 用于存储ring中的索引信息
const keyMap = {};
for(let i = 0; i < ring.length; i++) {
const k = ring[i];
if(keyMap[k]) {
keyMap[k].push(i)
} else {
keyMap[k] = [i]
}
}
// 缓存用于dfs剪枝
const memo = new Array(ring.length);
for(let i = 0; i < ring.length; i++) {
memo[i] = new Array(key.length).fill(-1)
}
// dfs递归
const dfs = ( ringI, keyI ) => {
if(keyI == key.length) return 0;
// 剪枝 有缓存直接返回缓存的结果
if( memo[ringI][keyI] !== -1 ) return memo[ringI][keyI]
const cur = key[keyI];
// 返回的结果
let res = Infinity;
for(const targetI of keyMap[cur]) {
// 正向位置
let d1 = Math.abs(ringI - targetI),
d2 = ring.length - d1;
const curMin = Math.min(d1, d2)
// 递归的循环不变式
res = Math.min(res, curMin + dfs(targetI, keyI+1))
}
memo[ringI][keyI] = res;
return res;
}
return dfs(0,0) + key.length;
};
动态规划,关键在于找到剪枝优化方案
2021.05.16
No.576 出界的路径数
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ,你可以将球移到相邻的单元格内,或者往上、下、左、右四个方向上移动使球穿过网格边界。但是,你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大,返回 结果 mod 109 + 7 的值。
示例 1:
输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6
解释:
示例 2:
输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12
解释:
说明:
球一旦出界,就不能再被移动回网格内。
网格的长度和高度在 [1,50] 的范围内。
N 在 [0,50] 的范围内。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/out-of-boundary-paths
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=576 lang=javascript
*
* [576] 出界的路径数
*/
// @lc code=start
/**
* @param {number} m
* @param {number} n
* @param {number} maxMove
* @param {number} startRow
* @param {number} startColumn
* @return {number}
*/
var findPaths = function(m, n, N, i, j) {
const helper = (i, j, N) => {
// N 次用完了,此时不能再走了就返回 0
if (N < 0) {
return 0
}
// 出界条件满足了,说明有一条出界路径,就返回 1
if (i < 0 || i >= m || j < 0 || j >= n) {
return 1
}
// 记忆化搜索(如果重复访问了那就用之前的值)
const key = `${i}-${j}-${N}`
if (visited.has(key)) {
return visited.get(key)
}
let res = 0
// 找上、下、左、右 四个方向
for (let k = 0; k < 4; k++) {
res = (res + helper(i + direction[k][0], j + direction[k][1], N -1)) % mod
}
// 将当前的值缓存下来
visited.set(key, res)
return res
}
const mod = Math.pow(10, 9) + 7
const direction = [[1, 0], [-1, 0], [0, -1], [0, 1]]
const visited = new Map()
return helper(i, j, N)
};
利用Map进行递归判断,状态转移是四个方向的探索
2021.05.17
No.980 不同路径-iii
在二维网格 grid 上,有 4 种类型的方格:
1 表示起始方格。且只有一个起始方格。
2 表示结束方格,且只有一个结束方格。
0 表示我们可以走过的空方格。
-1 表示我们无法跨越的障碍。
返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目。
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
示例 1:
输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出:2
解释:我们有以下两条路径:
- (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
- (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2:
输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出:4
解释:我们有以下四条路径:
- (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
- (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
- (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
- (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3:
输入:[[0,1],[2,0]]
输出:0
解释:
没有一条路能完全穿过每一个空的方格一次。
请注意,起始和结束方格可以位于网格中的任意位置。
提示:
1 <= grid.length * grid[0].length <= 20
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-paths-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=980 lang=javascript
*
* [980] 不同路径 III
*/
// @lc code=start
/**
* @param {number[][]} grid
* @return {number}
*/
var uniquePathsIII = function(grid) {
if(!grid.length) return 0;
const helper = ( grid, i, j, step ) => {
if( i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == -1 ) {
return 0;
}
if(grid[i][j] == 2) return step == -1 ? 1 : 0;
grid[i][j] = -1;
let res = 0;
// 向四个方向探索
res += helper( grid, i+1, j, step - 1 );
res += helper( grid, i, j+1, step - 1 );
res += helper( grid, i-1, j, step - 1 );
res += helper( grid, i, j-1, step - 1 );
grid[i][j] = 0
return res;
}
let startI = 0, startJ = 0, total = 0;
// 遍历
for( let i = 0; i < grid.length; i++ ) {
for( let j = 0; j < grid[i].length; j++ ) {
if( grid[i][j] == 1 ) {
startI = i;
startJ = j;
}
if( grid[i][j] == 0 ) {
total++;
}
}
}
return helper(grid, startI, startJ, total);
};
同576题,不同之处在于不能返回,动态规划进行四个方向的探索回溯
2021.05.18
No.1129 颜色交替的最短路径
在一个有向图中,节点分别标记为 0, 1, …, n-1。这个图中的每条边不是红色就是蓝色,且存在自环或平行边。
red_edges 中的每一个 [i, j] 对表示从节点 i 到节点 j 的红色有向边。类似地,blue_edges 中的每一个 [i, j] 对表示从节点 i 到节点 j 的蓝色有向边。
返回长度为 n 的数组 answer,其中 answer[X] 是从节点 0 到节点 X 的红色边和蓝色边交替出现的最短路径的长度。如果不存在这样的路径,那么 answer[x] = -1。
示例 1:
输入:n = 3, red_edges = [[0,1],[1,2]], blue_edges = []
输出:[0,1,-1]
示例 2:
输入:n = 3, red_edges = [[0,1]], blue_edges = [[2,1]]
输出:[0,1,-1]
示例 3:
输入:n = 3, red_edges = [[1,0]], blue_edges = [[2,1]]
输出:[0,-1,-1]
示例 4:
输入:n = 3, red_edges = [[0,1]], blue_edges = [[1,2]]
输出:[0,1,2]
示例 5:
输入:n = 3, red_edges = [[0,1],[0,2]], blue_edges = [[1,0]]
输出:[0,1,1]
提示:
1 <= n <= 100
red_edges.length <= 400
blue_edges.length <= 400
red_edges[i].length == blue_edges[i].length == 2
0 <= red_edges[i][j], blue_edges[i][j] < n
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/shortest-path-with-alternating-colors
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=1129 lang=javascript
*
* [1129] 颜色交替的最短路径
*/
// @lc code=start
/**
* @param {number} n
* @param {number[][]} red_edges
* @param {number[][]} blue_edges
* @return {number[]}
*/
var shortestAlternatingPaths = function(n, red_edges, blue_edges) {
var re_0=new Array(n).fill(Number.MAX_VALUE);
var re_1=new Array(n).fill(Number.MAX_VALUE);
var graph_red=new Array(n);
var graph_blue=new Array(n);
for(var i=0;i<n;i++){
graph_red[i]= new Array();
graph_blue[i]=new Array();
}
for(var i=0;i<red_edges.length;i++){
graph_red[red_edges[i][0]].push(red_edges[i][1]);
}
for(var i=0;i<blue_edges.length;i++){
graph_blue[blue_edges[i][0]].push(blue_edges[i][1]);
}
re_1[0]=0;
re_0[0]=0;
var now_b=[0],now_r=[0];
step=0;
while(now_b.length!==0 ||now_r.length!==0){
var new_b=[], new_r=[];
var point,adj;
step++;
while(now_b.length!==0){
point=now_b.pop();
adj=graph_red[point];
for(var next of adj){
if(re_0[next]===Number.MAX_VALUE){
re_0[next]=step;
new_r.push(next);
}
}
}
while(now_r.length!=0){
point=now_r.pop();
adj=graph_blue[point];
for(var next of adj){
if(re_1[next]===Number.MAX_VALUE){
re_1[next]=step;
new_b.push(next);
}
}
}
now_r=new_r;
now_b=new_b;
}
//console.log(re_0,re_1);
for(var i=0;i<n;i++){
re_0[i]=Math.min(re_0[i],re_1[i]);
if(re_0[i]===Number.MAX_VALUE) re_0[i]=-1;
}
return re_0;
};
Dijistra算法变形,使用动态规划进行逐步bfs
总结:
- 路径问题最常见的就是回溯探索,关键在于剪枝优化,对于状态转移函数的归纳总结;
- 动态规划是一种逐步处理问题的思路,常见的需要利用二维数组及hashMap等数据结构进行处理
股票问题
2021.05.19
No.121 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=3 lang=javascript
*
* [3] 无重复字符的最长子串
*/
// @lc code=start
/**
* @param {string} s
* @return {number}
*/
var lengthOfLongestSubstring = function(s) {
let max = 0, index = 0;
for(let i=0,j=0;j<s.length;j++) {
index = s.slice(i,j).indexOf(s[j]);
if(isRepeat(s.slice(i,j))) {
i += index + 1;
}
max = Math.max(max, j - i + 1)
}
return max;
function isRepeat(s) {
return s.length == Array.from(new Set(s.split(''))).length;
}
};
动态规划,股票问题i
2021.05.20
No.122 买卖股票的最佳时机-ii
给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=122 lang=javascript
*
* [122] 买卖股票的最佳时机 II
*/
// @lc code=start
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function(prices) {
let profit_in = -prices[0],
profit_out = 0,
n = prices.length;
for(let i =0; i < n; i++) {
profit_out = Math.max(profit_out, profit_in + prices[i]);
profit_in = Math.max(profit_in, profit_out - prices[i]);
}
return profit_out;
};
动态规划,股票问题ii
2021.05.21
No.123 买卖股票的最佳时机-iii
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1]
输出:0
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 105
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=123 lang=javascript
*
* [123] 买卖股票的最佳时机 III
*/
// @lc code=start
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function(prices) {
//第一次 买入, 卖出的利润
let profit_1_in = -prices[0], profit_1_out = 0;
//继第一次之后,第二次买入卖出的利润
let profit_2_in = -prices[0], profit_2_out = 0;
let n = prices.length;
for (let i = 1; i < n; i++){
profit_2_out = Math.max(profit_2_out, profit_2_in + prices[i]);
//第二次买入后的利润, 第一次卖出的利润 - prices[i]
profit_2_in = Math.max(profit_2_in, profit_1_out - prices[i]);
profit_1_out = Math.max(profit_1_out, profit_1_in + prices[i]);
//第一次买入后,利润为 -prices[i]
profit_1_in = Math.max(profit_1_in, -prices[i]);
}
return profit_2_out;
};
动态规划,股票问题iii
2021.05.24
No.188 买卖股票的最佳时机-iv
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3]
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=188 lang=javascript
*
* [188] 买卖股票的最佳时机 IV
*/
// @lc code=start
/**
* @param {number} k
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function(k, prices) {
let n = prices.length;
if (k > n / 2) {
k = Math.floor(n/2);
}
let profits = [];
for(let j=0; j <= k; j++) {
profits[j] = {
profits_out: 0,
profits_in: -prices[0]
}
}
for( let i = 0; i < n; i++ ) {
for( let j=1; j <= k; j++ ) {
profits[j] = {
profits_out: Math.max(profits[j][`profits_out`], profits[j][`profits_in`] + prices[i]),
profits_in: Math.max(profits[j][`profits_in`], profits[j-1][`profits_out`] - prices[i])
}
}
}
return profits[k][`profits_out`];
};
动态规划,股票问题iv
2021.05.26
No.309 最佳买卖股票时机含冷冻期
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
输入: [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=309 lang=javascript
*
* [309] 最佳买卖股票时机含冷冻期
*/
// @lc code=start
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function(prices) {
let n = prices.length,
profits_in = -prices[0],
profits_out = 0,
profits_freeze = 0;
for( let i = 0; i < prices.length; i++ ) {
let temp = profits_out;
profits_out = Math.max(profits_out, prices[i] + profits_in);
profits_in = Math.max(profits_in, profits_freeze - prices[i]);
profits_freeze = temp;
}
return profits_out;
};
动态规划,股票问题v
2021.05.27
No.714 买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中第 i 个元素代表了第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
示例 1:
输入:prices = [1, 3, 2, 8, 4, 9], fee = 2
输出:8
解释:能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
示例 2:
输入:prices = [1,3,7,5,10,3], fee = 3
输出:6
提示:
1 <= prices.length <= 5 * 104
1 <= prices[i] < 5 * 104
0 <= fee < 5 * 104
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=714 lang=javascript
*
* [714] 买卖股票的最佳时机含手续费
*/
// @lc code=start
/**
* @param {number[]} prices
* @param {number} fee
* @return {number}
*/
var maxProfit = function(prices, fee) {
let n = prices.length,
profits_in = 0 - prices[0],
profits_out = 0;
for( let i=0; i < prices.length; i++ ) {
profits_out = Math.max(profits_out, prices[i] + profits_in - fee);
profits_in = Math.max(profits_in, profits_out - prices[i]);
}
return profits_out < 0 ? 0 : profits_out;
};
动态规划,股票问题vi
总结:
- 股票问题关键在于对输入输出的状态进行判断转移,运用动态规划思想进行处理;
- 在动态规划实现中比较常见的是多维数组的逐步迭代,对于股票问题可以进行降维处理,优化效率
拆分组合
2021.05.31
No.132 分割回文串-ii
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文。
返回符合要求的 最少分割次数 。
示例 1:
输入:s = “aab”
输出:1
解释:只需一次分割就可将 s 分割成 [“aa”,“b”] 这样两个回文子串。
示例 2:
输入:s = “a”
输出:0
示例 3:
输入:s = “ab”
输出:1
提示:
1 <= s.length <= 2000
s 仅由小写英文字母组成
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/palindrome-partitioning-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=132 lang=javascript
*
* [132] 分割回文串 II
*/
// @lc code=start
/**
* @param {string} s
* @return {number}
*/
var minCut = function (s) {
let j, dp = new Array(s.length).fill(s.length)
for (let i = 0; i < s.length; i++) {
j = 0
while (i - j >= 0 && i + j < s.length) {
if (s[i - j] === s[i + j]) dp[i + j] = i - j === 0 ? 0 : dp[i + j] <= dp[i - j - 1] + 1 ? dp[i + j] : dp[i - j - 1] + 1
else break
j++
}
j = 0
while (i - j >= 0 && i + j + 1 < s.length) {
if (s[i - j] === s[i + j + 1]) dp[i + j + 1] = i - j === 0 ? 0 : dp[i + j + 1] <= dp[i - j - 1] + 1 ? dp[i + j + 1] : dp[i - j - 1] + 1
else break
j++
}
}
return dp[s.length - 1]
};
方案二:
/*
* @lc app=leetcode.cn id=132 lang=javascript
*
* [132] 分割回文串 II
*/
// @lc code=start
/**
* @param {string} s
* @return {number}
*/
var minCut = function (s) {
var manacher = function(s){
if(!s) return [];
var lstRadios=[];
//拼装manacher字符串
s=s.replace(/\w/g,(a)=>{return '#'+a;})+'#';
//三个指针,现在先定义中心指针c和最右指针r,剩下一个就是运动指针了
var r=-1, c=-1;
for(var i=0; i<s.length;i++){
//判断i在不在r右侧
//在,当前指针对应的半径无从判断,先赋值1
//不在,就判断当前i以c为中心的对应指针i'的半径,
//如果i'的半径超过了c半径的范围,就说明i的半径就为r-i+1;
//如果i'的半径刚好在c半径的的范围内,且不在边界上,那么i的半径就为i'的半径
//如果i'的半径刚好在c半径的指针上,那么i的半径是有可能再扩大的,需要再验证
lstRadios[i]=r>i?Math.min(lstRadios[2*c-i],r-i+1):1;
while(i+lstRadios[i]<s.length && i-lstRadios[i]>-1){
if(s.charAt(i-lstRadios[i]) == s.charAt(i+lstRadios[i]))lstRadios[i]++;
else break;
}
if(i+lstRadios[i]-1 > r){
r=1+lstRadios[i]-1;
c=i;
}
}
return lstRadios;
};
if(s.length<=1) return 0;
var lstRadios=manacher(s);
var dp=[];
for(var i=0; i<s.length; i++){
if(dp[i] == undefined) dp[i]=i;
if(i!=0)dp[i]=Math.min(dp[i-1]+1,dp[i]);
//先以i为中点
var d=lstRadios[2*i+1]/2 - 1;
for(var j=1; j<=d; j++){
if(dp[i+j] == undefined) dp[i+j]=i+j;
dp[i+j]=Math.min(((i-j-1)>=0?(dp[i-j-1]+1):0),dp[i+j]);
}
//以i和i+1的中间为中心
d=lstRadios[2*i+2]/2;
if(d<=0)continue;
for(var j=1; j<=d; j++){
if(dp[i+j] == undefined) dp[i+j]=i+j;
dp[i+j]=Math.min(((i-j)>=0?(dp[i-j]+1):0),dp[i+j]);
}
}
return dp[s.length-1];
};
方案三:
/*
* @lc app=leetcode.cn id=132 lang=javascript
*
* [132] 分割回文串 II
*/
// @lc code=start
/**
* @param {string} s
* @return {number}
*/
var minCut = function(s) {
const n = s.length;
const g = new Array(n).fill(0).map(() => new Array(n).fill(true));
for (let i = n - 1; i >= 0; --i) {
for (let j = i + 1; j < n; ++j) {
g[i][j] = s[i] == s[j] && g[i + 1][j - 1];
}
}
const f = new Array(n).fill(Number.MAX_SAFE_INTEGER);
for (let i = 0; i < n; ++i) {
if (g[0][i]) {
f[i] = 0;
} else {
for (let j = 0; j < i; ++j) {
if (g[j + 1][i]) {
f[i] = Math.min(f[i], f[j] + 1);
}
}
}
}
return f[n - 1];
};
动态规划,有三种不同的实现方案:1、利用字符串的位置特性,只用一遍动态规划;2、利用manacher进行一个查找的优化;3、两次动态规划
2021.06.01
No.1278 分割回文串-iii
给你一个由小写字母组成的字符串 s,和一个整数 k。
请你按下面的要求分割字符串:
首先,你可以将 s 中的部分字符修改为其他的小写英文字母。
接着,你需要把 s 分割成 k 个非空且不相交的子串,并且每个子串都是回文串。
请返回以这种方式分割字符串所需修改的最少字符数。
示例 1:
输入:s = “abc”, k = 2
输出:1
解释:你可以把字符串分割成 “ab” 和 “c”,并修改 “ab” 中的 1 个字符,将它变成回文串。
示例 2:
输入:s = “aabbc”, k = 3
输出:0
解释:你可以把字符串分割成 “aa”、“bb” 和 “c”,它们都是回文串。
示例 3:
输入:s = “leetcode”, k = 8
输出:0
提示:
1 <= k <= s.length <= 100
s 中只含有小写英文字母。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/palindrome-partitioning-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=1278 lang=javascript
*
* [1278] 分割回文串 III
*/
// @lc code=start
/**
* @param {string} s
* @param {number} k
* @return {number}
*/
var palindromePartition = function(s, k) {
const n = s.length;
const dp = Array.from({length: n}, () => Array(k+1).fill(100));
const cost = Array.from({length: n}, () => Array(n).fill(0));
for (let len = 1; len < n; len++) {
for (let i = 0; i < n - len; i++) {
const j = i + len;
cost[i][j] = cost[i+1][j-1] + (s[i] == s[j] ? 0 : 1);
}
}
for (let i = 0; i < n; i++) {
dp[i][1] = cost[0][i];
for (let kk = 2; kk <= k; kk++) {
for (let j = 0; j < i; j++) {
dp[i][kk] = Math.min(dp[i][kk], dp[j][kk-1] + cost[j+1][i]);
}
}
}
return dp[n-1][k];
};
方案二:
/*
* @lc app=leetcode.cn id=1278 lang=javascript
*
* [1278] 分割回文串 III
*/
// @lc code=start
/**
* @param {string} s
* @param {number} k
* @return {number}
*/
var palindromePartition = function (s, k) {
const m = s.length;
const dp = Array.from(Array(k), () => Array(m));
const map = Array.from(Array(m), () => Array(m));
const helper = (i, j) => {
const str = s.substring(i, j + 1);
let res = 0;
for (let l = 0; l < str.length / 2; l++)
if (str[l] !== str[str.length - 1 - l]) res++;
return res;
};
for (let i = 0; i < m; i++)
for (let j = i; j < m; j++) map[i][j] = helper(i, j);
for (let i = 0; i < k; i++) {
for (let j = i; j < m; j++) {
if (i === j || i === 0) {
dp[i][j] = map[i][j]; // No need to remove, each char is a substring
continue;
}
let res = Infinity;
for (let k = 1; j - k >= i - 1; k++)
res = Math.min(res, map[j + 1 - k][j] + dp[i - 1][j - k]);
dp[i][j] = res;
}
}
return dp[k - 1][m - 1];
};
两次dp,方法2对字符串进行了过滤截取
2021.06.02
No.1745 回文串分割-iv
给你一个字符串 s ,如果可以将它分割成三个 非空 回文子字符串,那么返回 true ,否则返回 false 。
当一个字符串正着读和反着读是一模一样的,就称其为 回文字符串 。
示例 1:
输入:s = “abcbdd”
输出:true
解释:“abcbdd” = “a” + “bcb” + “dd”,三个子字符串都是回文的。
示例 2:
输入:s = “bcbddxy”
输出:false
解释:s 没办法被分割成 3 个回文子字符串。
提示:
3 <= s.length <= 2000
s 只包含小写英文字母。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/palindrome-partitioning-iv
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=1745 lang=javascript
*
* [1745] 回文串分割 IV
*/
// @lc code=start
/**
* @param {string} s
* @return {boolean}
*/
var checkPartitioning = function(s) {
let dp = new Array(s.length);
for (let i = 0; i < dp.length; i++) {
dp[i] = new Array(s.length).fill(true);
}
for (let i = s.length - 1; i >=0 ;i--) {
for (let j = i; j < s.length; j++) {
if (i !== j) {
dp[i][j] = (s[i] == s[j]) && dp[i + 1][j - 1];
}
}
}
for (let i = 0; i < s.length - 2; i++) {
if(dp[0][i] == false) continue;
for (let j = i + 1; j < s.length - 1; j++) {
if(dp[i+1][j] == false || dp[j + 1][s.length - 1] == false ) continue;
if (dp[0][i] && dp[i + 1][j] && dp[j + 1][s.length - 1]) {
return true;
}
}
}
return false;
};
动态规划,对循环可进行提前判断
2021.07.02
No.139 单词拆分
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以被拆分成 “leet code”。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以被拆分成 “apple pen apple”。
注意你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/word-break
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=139 lang=javascript
*
* [139] 单词拆分
*/
// @lc code=start
/**
* @param {string} s
* @param {string[]} wordDict
* @return {boolean}
*/
var wordBreak = function(s, wordDict) {
const n = s.length;
const wordDictSet = new Set(wordDict);
const dp = new Array(n + 1).fill(false);
dp[0] = true;
for (let i = 1; i <= n; i++) {
for (let j = 0; j < i; j++) {
if (dp[j] && wordDictSet.has(s.substr(j, i - j))) {
dp[i] = true;
break;
}
}
}
return dp[n];
};
典型动态规划问题,通过dp[i]确定切割位置
2021.07.07
No.140 单词拆分-ii
给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,在字符串中增加空格来构建一个句子,使得句子中所有的单词都在词典中。返回所有这些可能的句子。
说明:
分隔时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
输入:
s = “catsanddog”
wordDict = [“cat”, “cats”, “and”, “sand”, “dog”]
输出:
[
“cats and dog”,
“cat sand dog”
]
示例 2:
输入:
s = “pineapplepenapple”
wordDict = [“apple”, “pen”, “applepen”, “pine”, “pineapple”]
输出:
[
“pine apple pen apple”,
“pineapple pen apple”,
“pine applepen apple”
]
解释: 注意你可以重复使用字典中的单词。
示例 3:
输入:
s = “catsandog”
wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出:
[]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/word-break-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=140 lang=javascript
*
* [140] 单词拆分 II
*/
// @lc code=start
/**
* @param {string} s
* @param {string[]} wordDict
* @return {string[]}
*/
var wordBreak = function(s, wordDict) {
let dp = new Array(s.length + 1).fill(false)
dp[0] = true
for (let i = 1; i <= s.length; i++) {
for (let j = 0; j <= i; j++) {
if (dp[j] && wordDict.indexOf(s.slice(j, i)) >= 0) {
dp[i] = true
break
}
}
}
if(!dp[s.length]) return []
let ans = []
function backTrack(cur, str) {
if(str.length == 0) {
ans.push(cur)
return
}
for(let i = 0; i < str.length; i++) {
if(wordDict.indexOf(str.slice(0, i + 1)) >= 0) {
if(cur.length > 0) backTrack(cur + ' ' + str.slice(0, i + 1), str.slice(i + 1))
else backTrack(str.slice(0, i + 1), str.slice(i + 1))
}
}
}
backTrack('', s)
return ans
};
方案二:
/*
* @lc app=leetcode.cn id=140 lang=javascript
*
* [140] 单词拆分 II
*/
// @lc code=start
/**
* @param {string} s
* @param {string[]} wordDict
* @return {string[]}
*/
var wordBreak = function(s, wordDict) {
// 辅助函数
const backtrack = (s, length, wordSet, index, map) => {
if (map.has(index)) {
return map.get(index);
}
const wordBreaks = [];
if (index === length) {
wordBreaks.push([]);
}
for (let i = index + 1; i <= length; i++) {
const word = s.substring(index, i);
if (wordSet.has(word)) {
const nextWordBreaks = backtrack(s, length, wordSet, i, map);
for (const nextWordBreak of nextWordBreaks) {
const wordBreak = [word, ...nextWordBreak]
wordBreaks.push(wordBreak);
}
}
}
map.set(index, wordBreaks);
return wordBreaks;
}
const map = new Map();
const wordBreaks = backtrack(s, s.length, new Set(wordDict), 0, map);
const breakList = [];
for (const wordBreak of wordBreaks) {
breakList.push(wordBreak.join(' '));
}
return breakList;
};
有两种方案:1、借助139题先进行判断,然后再进行回溯;2、利用Map数据结构,直接回溯
2021.07.08
No.343 整数拆分
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/integer-break
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=343 lang=javascript
*
* [343] 整数拆分
*/
// @lc code=start
/**
* @param {number} n
* @return {number}
*/
var integerBreak = function(n) {
// 利用均值不等式 x1 * x2 * ··· * xn ≤ ( ( x1 + x2 + ··· + xn ) / n )^n
let max = -Infinity;
for( let i = 2; i <= n; i++ ) {
let v = -Infinity;
if(n % i == 0) {
v = Math.pow(n/i,i)
} else {
let v1 = Math.ceil(n/i),
v2 = Math.floor(n/i)
v = Math.max(
Math.pow(v1,i-1) * (n - v1*(i-1)) ,
Math.pow(v2,i-1) * (n - v2*(i-1))
)
}
max = Math.max(v, max)
}
return max;
};
方案二:
/*
* @lc app=leetcode.cn id=343 lang=javascript
*
* [343] 整数拆分
*/
// @lc code=start
/**
* @param {number} n
* @return {number}
*/
var integerBreak = function(n) {
const dp = new Array(n + 1);
dp[1] = 1;
dp[2] = 1;
for (let i = 3; i <= n; i++) {
dp[i] = 0;
// 对于数字 i,它可以分为两份:j 和 i-j,j 的范围是 1 到 i-j
for (let j = 1; j <= i - j; j++) {
// 对于 i-j 这部分可以拆或不拆,不拆就是 i-j,拆就是 dp[i-j]
dp[i] = Math.max(dp[i], j * (i - j), j * dp[i - j]);
}
}
return dp[n];
};
有两种方案:1、数学方案,利用均值不等式进行判断处理;2、动态规划
2021.07.09
No.410 分割数组的最大值
给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。
示例 1:
输入:nums = [7,2,5,10,8], m = 2
输出:18
解释:
一共有四种方法将 nums 分割为 2 个子数组。 其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18,在所有情况中最小。
示例 2:
输入:nums = [1,2,3,4,5], m = 2
输出:9
示例 3:
输入:nums = [1,4,4], m = 3
输出:4
提示:
1 <= nums.length <= 1000
0 <= nums[i] <= 106
1 <= m <= min(50, nums.length)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/split-array-largest-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=410 lang=javascript
*
* [410] 分割数组的最大值
*/
// @lc code=start
/**
* @param {number[]} nums
* @param {number} m
* @return {number}
*/
var splitArray = function(nums, m) {
let max = 0
sum = 0;
for (let i = 0; i < nums.length; i++) {
if (max < nums[i]) max = nums[i];
sum += nums[i];
}
while (max < sum) {
let mid = parseInt((sum - max) / 2, 10) + max;
// 随机选择的值成立则这个值默认为最大的可能结果继续查找
if (check(nums, mid, m)) {
sum = mid;
} else {
// 不满足,重置最小可能结果
max = mid + 1;
}
}
function check(nums, val, m) {
let sum = 0,
index = 1;
for (let i = 0; i < nums.length; i++) {
// 如果分段和大于了假设的结果说明,i是该分段的终点,形成一个分段
// index记录+1,i就成了下一个分段的起点(重置sum)开始校验下一个分段
if (sum + nums[i] > val) {
index++;
sum = nums[i];
} else {
sum += nums[i];
}
}
// 如果index即分段数量满足小于等于m则说明这个假设值成立
return index <= m;
}
// 返回最小可能结果
return max;
};
方案二:
/*
* @lc app=leetcode.cn id=410 lang=javascript
*
* [410] 分割数组的最大值
*/
// @lc code=start
/**
* @param {number[]} nums
* @param {number} m
* @return {number}
*/
var splitArray = function(nums, m) {
let len = nums.length,
sumList = Array(len + 1).fill(0),
dp = Array.from({ length: len + 1 }, () => Array(m + 1).fill(Number.MAX_VALUE));
// 逐位增加,反面后面根据区间求区间和
for (let i = 0; i < len; i++) {
sumList[i + 1] = sumList[i] + nums[i];
}
// 默认值
dp[0][0] = 0;
for (let i = 1; i <= len; i++) {
for (let j = 1; j <= Math.min(m, i); j++) {
// 前i个数分成j段
for (let x = j - 1; x < i; x++) {
// x最后一段的起点
// perv本轮分割完成 分段中最大的和
let prev = Math.max(dp[x][j - 1], sumList[i] - sumList[x])
// 该分割情况下最大分段和的最小值
dp[i][j] = Math.min(prev, dp[i][j])
}
}
}
return dp[len][m]
};
有两种方案:1、二分法;2、动态规划
2021.07.11
No.413 等差数列划分
如果一个数列至少有三个元素,并且任意两个相邻元素之差相同,则称该数列为等差数列。
例如,以下数列为等差数列:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
以下数列不是等差数列。
1, 1, 2, 5, 7
数组 A 包含 N 个数,且索引从0开始。数组 A 的一个子数组划分为数组 (P, Q),P 与 Q 是整数且满足 0<=P
如果满足以下条件,则称子数组(P, Q)为等差数组:
元素 A[P], A[p + 1], …, A[Q - 1], A[Q] 是等差的。并且 P + 1 < Q 。
函数要返回数组 A 中所有为等差数组的子数组个数。
示例:
A = [1, 2, 3, 4]
返回: 3, A 中有三个子等差数组: [1, 2, 3], [2, 3, 4] 以及自身 [1, 2, 3, 4]。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/arithmetic-slices
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=413 lang=javascript
*
* [413] 等差数列划分
*/
// @lc code=start
/**
* @param {number[]} nums
* @return {number}
*/
var numberOfArithmeticSlices = function(nums) {
// 判断是否是等差数列
const isArithmetic = arr => {
const diff = arr[1] - arr[0];
for( let p = 0, q = p+ 1; p < arr.length -1; p++, q++ ) {
if( arr[q] - arr[p] != diff ) {
return false;
}
}
return true;
}
// 返回的个数
let n = 0;
for(let a = 0; a < nums.length - 2;a++ ) {
for(let b = a + 2; b < nums.length; ) {
if(!isArithmetic(nums.slice(a,b+1))) {
break;
} else {
n++;
b++
}
}
}
return n;
};
方案二:
/*
* @lc app=leetcode.cn id=413 lang=javascript
*
* [413] 等差数列划分
*/
// @lc code=start
/**
* @param {number[]} nums
* @return {number}
*/
var numberOfArithmeticSlices = function(nums) {
let len = nums.length
if (len < 3) {
return 0
}
let dp = Array(len).fill(0)
for (let i = 2;i <= len;i++) {
if (nums[i] - nums[i - 1] === nums[i - 1] - nums[i - 2]) {
dp[i] = dp[i - 1] + 1
}
}
return dp.reduce((prev, cur) => { return prev + cur }, 0)
};
有两种方案:1、暴解;2、动态规划
2021.07.12
No.416 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/partition-equal-subset-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=416 lang=javascript
*
* [416] 分割等和子集
*/
// @lc code=start
/**
* @param {number[]} nums
* @return {boolean}
*/
var canPartition = function(nums) {
if(nums.length < 2) return false;
const sum = nums.reduce((prev, curr) => prev + curr);
if( sum % 2 !== 0) {
return false;
}
const target = sum / 2;
nums.sort((a,b) => b-a);
if(nums[0] > target) {
return false;
}
// 动态规划
const dp = new Array(nums.length).fill(0).map(v => new Array(target + 1, false));
for (let i = 0; i < nums.length; i++) {
dp[i][0] = true;
}
dp[0][nums[0]] = true;
for (let i = 1; i < nums.length; i++) {
const num = nums[i];
for (let j = 1; j <= target; j++) {
if (j >= num) {
dp[i][j] = dp[i - 1][j] | dp[i - 1][j - num];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return dp[nums.length - 1][target];
};
NP完全,可转化为0-1背包问题,动态规划解决
2021.07.13
No.446 等差数列拆分 ii-子序列
如果一个数列至少有三个元素,并且任意两个相邻元素之差相同,则称该数列为等差数列。
例如,以下数列为等差数列:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
以下数列不是等差数列。
1, 1, 2, 5, 7
数组 A 包含 N 个数,且索引从 0 开始。该数组子序列将划分为整数序列 (P0, P1, …, Pk),满足 0 ≤ P0 < P1 < … < Pk < N。
如果序列 A[P0],A[P1],…,A[Pk-1],A[Pk] 是等差的,那么数组 A 的子序列 (P0,P1,…,PK) 称为等差序列。值得注意的是,这意味着 k ≥ 2。
函数要返回数组 A 中所有等差子序列的个数。
输入包含 N 个整数。每个整数都在 -231 和 231-1 之间,另外 0 ≤ N ≤ 1000。保证输出小于 231-1。
示例:
输入:[2, 4, 6, 8, 10]
输出:7
解释:
所有的等差子序列为:
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/arithmetic-slices-ii-subsequence
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=446 lang=javascript
*
* [446] 等差数列划分 II - 子序列
*/
// @lc code=start
/**
* @param {number[]} nums
* @return {number}
*/
var numberOfArithmeticSlices = function(nums) {
// 定义 i 的数组
let dp = Array(nums.length).fill(0).map(x=> new Object())
let ans = 0
for(let i=1; i<nums.length; ++i){
for(let j=0; j<i; ++j){
let sub = nums[i] - nums[j]
// 定义 sub 的键值对 [], 第0位代表序列长度为 2,从第1位开始满足题意要求
if(!(sub in dp[i])){
dp[i][sub] = [0]
}
dp[i][sub][0] += 1
if(sub in dp[j]){
for(let k=0; k<dp[j][sub].length; ++k){
if(dp[i][sub][k+1] === undefined) dp[i][sub][k+1] = 0
dp[i][sub][k+1] += dp[j][sub][k]
ans += dp[j][sub][k]
}
}
}
}
return ans
};
动态规划
2021.07.14
No.698 划分为k个相等的子集
给定一个整数数组 nums 和一个正整数 k,找出是否有可能把这个数组分成 k 个非空子集,其总和都相等。
示例 1:
输入: nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出: True
说明: 有可能将其分成 4 个子集(5),(1,4),(2,3),(2,3)等于总和。
提示:
1 <= k <= len(nums) <= 16
0 < nums[i] < 10000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/partition-to-k-equal-sum-subsets
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=698 lang=javascript
*
* [698] 划分为k个相等的子集
*/
// @lc code=start
/**
* @param {number[]} nums
* @param {number} k
* @return {boolean}
*/
var canPartitionKSubsets = function(nums, k) {
const sum = nums.reduce((prev, curr) => prev + curr);
if( sum % k !== 0 ) return false;
const target = sum / k;
nums.sort((a,b) => b - a);
if(nums[0] > target) return false;
// 动态规划
const MAX_STATE = (1 << nums.length) - 1 // 1 <= N <= 16
let dp = new Array(MAX_STATE + 1).fill(null)
dp[0] = 0
// 枚举所有状态,递推
for (let state = 1; state <= MAX_STATE; ++state) { // O(2^N)
for (let i = 0; i < nums.length; ++i) { // O(N)
const iBit = 1 << i
// 如果 state 表示未选取 nums[i] ,说明不能达到 (state, i) 状态
if ((state & iBit) === 0) continue
const prevState = state ^ iBit
// NOTICE: 如果不能到达 prevState 状态
if (dp[prevState] === null) continue
const prevSubsetSum = dp[prevState] % target
// 最优性剪枝优化:nums 已升序排序,如果 nums[i] 已偏大,后续更加偏大,无需尝试
if (prevSubsetSum + nums[i] > target) break
dp[state] = dp[prevState] + nums[i]
}
}
// console.log(dp)
return dp[MAX_STATE] === sum
};
方案二:
/*
* @lc app=leetcode.cn id=698 lang=javascript
*
* [698] 划分为k个相等的子集
*/
// @lc code=start
/**
* @param {number[]} nums
* @param {number} k
* @return {boolean}
*/
var canPartitionKSubsets = function(nums, k) {
const sum = nums.reduce((prev, curr) => prev + curr);
if( sum % k !== 0 ) return false;
const target = sum / k;
nums.sort((a,b) => b - a);
if(nums[0] > target) return false;
// 回溯
const sums = new Array(k).fill(0);
const helper = (i, sums, target, nums, k) => {
if(i === nums.length) return true;
for( let j = 0; j< k; j++ ) {
if(sums[j] < target && nums[i] + sums[j] <= target) {
sums[j] += nums[i];
if(helper(i+1, sums, target, nums, k)) {
return true;
}
sums[j] -= nums[i];
}
}
return false;
}
return helper(0,sums, target, nums, k);
};
有两种方案:1、动态规划,用二进制对数组进行表示;2、回溯递归
2021.07.15
No.902 最大为N的数字组合
我们有一组排序的数字 D,它是 {‘1’,‘2’,‘3’,‘4’,‘5’,‘6’,‘7’,‘8’,‘9’} 的非空子集。(请注意,‘0’ 不包括在内。)
现在,我们用这些数字进行组合写数字,想用多少次就用多少次。例如 D = {‘1’,‘3’,‘5’},我们可以写出像 ‘13’, ‘551’, ‘1351315’ 这样的数字。
返回可以用 D 中的数字写出的小于或等于 N 的正整数的数目。
示例 1:
输入:D = [“1”,“3”,“5”,“7”], N = 100
输出:20
解释:
可写出的 20 个数字是:
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.
示例 2:
输入:D = [“1”,“4”,“9”], N = 1000000000
输出:29523
解释:
我们可以写 3 个一位数字,9 个两位数字,27 个三位数字,
81 个四位数字,243 个五位数字,729 个六位数字,
2187 个七位数字,6561 个八位数字和 19683 个九位数字。
总共,可以使用D中的数字写出 29523 个整数。
提示:
D 是按排序顺序的数字 ‘1’-‘9’ 的子集。
1 <= N <= 10^9
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/numbers-at-most-n-given-digit-set
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案一:
/*
* @lc app=leetcode.cn id=902 lang=javascript
*
* [902] 最大为 N 的数字组合
*/
// @lc code=start
/**
* @param {string[]} digits
* @param {number} n
* @return {number}
*/
var atMostNGivenDigitSet = function(digits, n) {
digits.sort((a,b) => Number(a) - Number(b))
// 获取n的位数
const UNIT = (n + '').length;
console.log('UNIT', UNIT)
// 获取n对应位置数组
const queue = (n + '').split('');
let sum = 0;
for(let i = 1; i < UNIT; i++) {
sum += Math.pow(digits.length, i)
}
// 辅助函数
const helper = (pos, queue, digits) => {
if (pos === queue.length) {
return 1;
}
let count = 0;
for (let i = 0; i < digits.length; i++) {
if (digits[i] < queue[pos]) {
count += Math.pow(digits.length, queue.length - pos - 1);
} else if (digits[i] == queue[pos]) {
count += helper(pos + 1, queue, digits);
} else {
break;
}
}
return count;
}
sum += helper(0, queue, digits)
return sum;
};
方案二:
/*
* @lc app=leetcode.cn id=902 lang=javascript
*
* [902] 最大为 N 的数字组合
*/
// @lc code=start
/**
* @param {string[]} digits
* @param {number} n
* @return {number}
*/
var atMostNGivenDigitSet = function(digits, n) {
const s = n + '';
const K = s.length;
const dp = new Array(K+1).fill(0);
dp[K] = 1;
for(let i = K -1; i >= 0; --i) {
let si = s[i];
for(let j=0; j < digits.length; j++) {
if(digits[j] < si) {
dp[i] += Math.pow(digits.length, K-i-1)
} else if(digits[j] == si) {
dp[i] += dp[i+1];
}
}
}
for(let k=1; k< K; ++k) {
dp[0] += Math.pow(digits.length, k)
}
return dp[0]
};
有两种方案:1、递归;2、动态规划
2021.07.16
No.923 三数之和的多种可能
给定一个整数数组 A,以及一个整数 target 作为目标值,返回满足 i < j < k 且 A[i] + A[j] + A[k] == target 的元组 i, j, k 的数量。
由于结果会非常大,请返回 结果除以 10^9 + 7 的余数。
示例 1:
输入:A = [1,1,2,2,3,3,4,4,5,5], target = 8
输出:20
解释:
按值枚举(A[i],A[j],A[k]):
(1, 2, 5) 出现 8 次;
(1, 3, 4) 出现 8 次;
(2, 2, 4) 出现 2 次;
(2, 3, 3) 出现 2 次。
示例 2:
输入:A = [1,1,2,2,2,2], target = 5
输出:12
解释:
A[i] = 1,A[j] = A[k] = 2 出现 12 次:
我们从 [1,1] 中选择一个 1,有 2 种情况,
从 [2,2,2,2] 中选出两个 2,有 6 种情况。
提示:
3 <= A.length <= 3000
0 <= A[i] <= 100
0 <= target <= 300
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/3sum-with-multiplicity
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
方案:
/*
* @lc app=leetcode.cn id=923 lang=javascript
*
* [923] 三数之和的多种可能
*/
// @lc code=start
/**
* @param {number[]} arr
* @param {number} target
* @return {number}
*/
var threeSumMulti = function(arr, target) {
console.log('arr', arr.length)
// mod数
const mod = (10**9)+7;
// 阶乘
const factorial = n => {
if (0 === n) {
return 1;
}
let res = 1;
for (let i = 1; i <= n; ++i) {
res *= i;
}
return res;
}
// Cmn函数
const combination = (m,n) => {
let s = 1;
for(let i =0;i< n;i++) {
s *= (m - i);
}
return s / factorial(n)
}
console.log('combination', combination(3000,3))
// 数组去重 并按从小到大排序
const _ = Array.from(new Set(arr)).sort((a,b) => a-b);
const LEN = _.length,
MAX = _[LEN-1],
MIN = _[0];
console.log('_', _)
// 在去重数组中去选择符合要求的三个数
let i = 0,
j = LEN - 1,
m = ~~((i+j)/2);
// r用于存储符合要求的数组
const r = [];
for(let i=0; i < LEN; i++) {
let j= LEN -1;
for(let m = i; m <= j;) {
if(_[i]+_[m]+_[j] == target) {
r.push([_[i], _[m], _[j]])
}
if(_[i]+_[m]+_[j]>target && m < j) {
j--;
m--
}
m++
}
}
console.log('r', r)
// 构建值对应数量的map
const map = {};
for(let num = 0; num < LEN; num++) {
let key = _[num],
value = arr.filter(f => f == key).length;
map[key] = value;
}
console.log('map', map)
// 对r进行排查
let sum = 0;
r.forEach(item => {
if(item[0] == item[1] && item[1] == item[2]) {
if(map[`${item[0]}`] >= 3) {
console.log('走了 A A A')
sum += combination(map[`${item[0]}`], 3)
}
} else if(item[0] != item[1] && item[1] == item[2]) {
if(map[`${item[1]}`] >= 2) {
console.log('走了 A B B')
sum += combination(map[`${item[0]}`], 1)*combination(map[`${item[1]}`], 2)
}
} else if(item[0] == item[1] && item[1] != item[2]) {
if(map[`${item[0]}`] >= 2) {
console.log('走了 A A B')
sum += combination(map[`${item[0]}`], 2)*combination(map[`${item[2]}`], 1)
}
} else if(item[0] != item[1] && item[1] != item[2] && item[0] != item[2]) {
console.log('走了 A B C')
sum += combination(map[`${item[0]}`], 1)*combination(map[`${item[1]}`], 1)*combination(map[`${item[2]}`], 1)
}
})
console.log('sum', sum)
return sum % mod;
};
三指针法,阶乘可进行动态规划实现
总结:
- 拆分组合问题关键在于对问题的转移方程定义及建模,将状态可以逐步转移,从而解决问题;
- 在状态方程建立过程中,常常需要结合其他常见方法如指针、递归等方法来进行优化