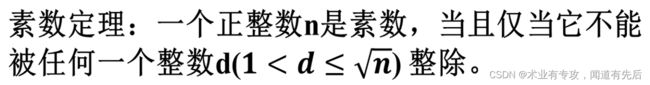第四章——密码学的数学引论

一.数论

1.素数

 200以内的素数：
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199

算术基本定理：

任何一个不等于0的正整数a都可以写成唯一的表达式a＝P1α1P2α2…Ptαt，这里P1＜P2＜P3…＜Pt是素数，其中αi>0.

eg. 91 = 7 × 13 ; 3600 = 24 × 32 × 52

根据定理，17是素数，18不是素数。

欧几里得算法——求最大公约数

基本思想：

为了求两个正整数a,b的最大公约数，首先将两个正整数中较大者赋给 a ，较小者赋给b, 然后循环使用R=a mod b ， 直到模运算的余数b=0结束，则前一个余数就是二者的最大公约数。

证明：a=kb+r≡r mod b    →  a mod b=a-kb 

          设d是a，b的公因子，即d|a , d|b, 所以d|kb.

          由d|a和d|kb，得d|(a mod b)，   故d是b和a mod b的公因子。

a和b的公因子集合与b和(a mod b)的公因子集合相同，故它们两组的最大公因子也相同。 

                                  gcd(55,22)=gcd(22,11)=gcd(11,0)=11
                                  gcd(11,10)=gcd(10,1)=1

                                                   gcd(1970,1066)的计算过程

轮序	x	y	R
1	1970	1066	904
2	1066	904	162
3	904	162	94
4	162	94	68
5	94	68	26
6	68	26	16
7	26	16	10
8	16	10	6
9	10	6	4
10	6	4	2
11	4	2	0
12	2	0

因此，gcd(1970,1066)=2

算法实现：

def gcd(a,b):
# *************begin************#
    if a

扩展的欧几里得算法——求乘法逆元

参考文章：扩展欧几里得算法求逆元python代码实现(含递归与非递归算法)_扩展欧几里得算法 非递归-CSDN博客

基本思想 ：

扩展欧几里得算法是欧几里得算法（又叫辗转相除法）的扩展。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与 b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。因此，有两个数a,b，对它们进行辗转相除法，可得它们的最大公约数；然后，收集辗转相除法中产生的式子，倒回去，可以得到ax+by=gcd(a,b)的一组整数特解。

以下是扩展欧几里得算法的python实现：

算法实现：

1.递归
 

#扩展欧几里得算法 
def ext_gcd(a, b):    
    if b == 0:          
        return 1, 0, a     
    else:         
        x, y, gcd = ext_gcd(b, a % b) #递归直至余数等于0(需多递归一层用来判断)        
        x, y = y, (x - (a // b) * y) #辗转相除法反向推导每层a、b的因子使得gcd(a,b)=ax+by成立         
        return x, y, gcd

 2.非递归

print("请输入一个整数：")
a = int(input())
print("请输入模？")
m = int(input())

if a < m:
    a, m = m, a
    x1, x2,x3= 1, 0, a
    y1, y2,y3= 0, 1, m
    while y3 != 0:
        Q = x3//y3
        t1, t2, t3 = x1 - Q*y1, x2 - Q*y2, x3 - Q*y3
        x1, x2, x3 = y1, y2, y3
        y1, y2, y3 = t1, t2, t3
    print(x2)
else:
    x1, x2, x3 = 1, 0, a
    y1, y2, y3 = 0, 1, m
    while y3 != 0:
        Q = x3 // y3
        t1, t2, t3 = x1 - Q*y1, x2 - Q*y2, x3 - Q*y3
        x1, x2, x3 = y1, y2, y3
        y1, y2, y3 = t1, t2, t3
    print(x1)

以下是两种方法的运行验证结果

 

说明以上代码正确有效。