分治算法——快排 | 归并思想
文章目录
- 一、快排思想
-
- 1. leetcode75. 颜色分类
- 2. leetcode912. 排序数组
- 3. leetcode215. 数组中的第K个最大元素
- 4. leetcode面试题17.14. 最小K个数
- 二、归并思想
-
- 1. leetcode912. 排序数组
- 2. leetcodeLCR 170. 交易逆序对的总数
- 3. 计算右侧小于当前元素的个数
- 4. 翻转对
一、快排思想
当一个数组中的元素重复率特别高的时候,经典的快速排序算法是不适合的。它会导致时间复杂度由O(logN)上升为O(N^2),这里我们可以使用三项切分的方式来实现快速排序算法,所谓的三项切分,就是把等于基准值的元素放在中间,大于基准值的元素和小于基准值的分别放两边,这样数组分成了三分,比起普通的快速排序,当数据中的重复元素特别多时,效率将会大大提升。
单趟排序的过程:
1. leetcode75. 颜色分类
代码实现:
class Solution {
public:
void sortColors(vector<int>& nums) {
int left = -1, right = nums.size();
for(int i = 0; i < right;)
{
if(nums[i] == 0)
swap(nums[++left], nums[i++]);
else if(nums[i] == 1)
i++;
else
swap(nums[--right], nums[i]);
}
}
};
2. leetcode912. 排序数组
代码实现:
class Solution {
public:
int getRandom(const vector<int>& nums, int left, int right){
int r = rand();
return nums[r % (right - left + 1) + left];
}
void qsort(vector<int>& nums, int l, int r)
{
if(l > r) return;
int key = getRandom(nums, l, r);
int i = l, left = l - 1, right = r + 1;
while(i < right)
{
if(nums[i] < key)
swap(nums[++left], nums[i++]);
else if(nums[i] == key)
i++;
else
swap(nums[--right], nums[i]);
}
// 递归左右子区间
qsort(nums, l, left);
qsort(nums, right, r);
}
vector<int> sortArray(vector<int>& nums) {
srand(time(NULL));
qsort(nums, 0, nums.size() - 1);
return nums;
}
};
3. leetcode215. 数组中的第K个最大元素
代码实现:
class Solution {
public:
int getRandom(const vector<int>& nums, int left, int right){
return nums[rand()%(right - left + 1) + left];
}
// 快速选择算法
int qsort(vector<int>& nums, int l, int r, int k)
{
if(l == r) return nums[l];
int key = getRandom(nums, l, r);
int i = l, left = l - 1, right = r + 1;
while(i < right)
{
if(nums[i] < key) swap(nums[++left], nums[i++]);
else if(nums[i] == key) i++;
else swap(nums[--right], nums[i]);
}
// 重点代码
int c = r - right + 1, b = right - left - 1;
if(c >= k) return qsort(nums, right, r, k);
else if(b + c >= k) return key;
else return qsort(nums, l, left, k - b - c);
}
int findKthLargest(vector<int>& nums, int k) {
srand(time(0));
return qsort(nums, 0, nums.size() - 1, k);
}
};
4. leetcode面试题17.14. 最小K个数
代码实现:
class Solution {
public:
int getRandom(const vector<int>& nums, int left, int right){
int r = rand();
return nums[r % (right - left + 1) + left];
}
void qsort(vector<int>& arr, int l, int r, int k)
{
if(l >= r) return;
int key = getRandom(arr, l, r);
int i = l, left = l - 1, right = r + 1;
while(i < right)
{
if(arr[i] < key) swap(arr[++left], arr[i++]);
else if(arr[i] == key) i++;
else swap(arr[--right], arr[i]);
}
// 核心代码
int a = left - l + 1, b = right - left - 1;
if(a > k) qsort(arr, l, left, k);
else if(a + b >= k) return;
else qsort(arr, right, r, k - a - b);
}
vector<int> smallestK(vector<int>& arr, int k) {
srand(time(0));
qsort(arr, 0, arr.size() - 1, k);
return {arr.begin(), arr.begin() + k};
}
};
二、归并思想
归并排序算法是采用 分治法(Divide and Conquer) 的一个非常典型的应用,且各层分治递归可以同时进行。
首先把一个未排序的序列从中间分割成2部分,再把2部分分成4部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
1. leetcode912. 排序数组
代码实现:
class Solution {
vector<int> tmp;
public:
void mergeSort(vector<int>& nums, int left, int right)
{
if(left >= right) return;
int mid = (left + right) >> 1;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur1] < nums[cur2]) tmp[i++] = nums[cur1++];
else tmp[i++] = nums[cur2++];
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int i = left; i <= right; i++) nums[i] = tmp[i - left];
}
vector<int> sortArray(vector<int>& nums) {
tmp.resize(nums.size());
mergeSort(nums, 0, (int)nums.size() - 1);
return nums;
}
};
2. leetcodeLCR 170. 交易逆序对的总数
解题思路:
这里我们可以采用分治的思想来解决这道问题,与归并排序不同的是,这里我们使用降序的方式进行归并排序,将序列从中间分开,将逆序对分成三类:
因此我们解决问题的思路可以转换为一下方式:
- 递归算左边的;
- 递归算右边的;
- 算一个左一个右的;
- 把他们加到到一起。
代码实现:
class Solution {
public:
vector<int> tmp;
int MergeSort(vector<int>& record, int left, int right)
{
if(left >= right) return 0;
int mid = (left + right) >> 1;
int res = MergeSort(record, left, mid) + MergeSort(record, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur1 <= mid && cur2 <= right)
{
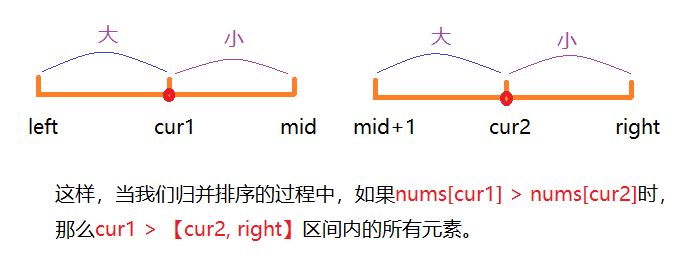
if(record[cur1] > record[cur2]){
res += (right - cur2 + 1);
tmp[i++] = record[cur1++];
}else{
tmp[i++] = record[cur2++];
}
}
while(cur1 <= mid) tmp[i++] = record[cur1++];
while(cur2 <= right) tmp[i++] = record[cur2++];
for(int i = left; i <= right; i++) record[i] = tmp[i - left];
return res;
}
int reversePairs(vector<int>& record) {
tmp.resize(record.size());
return MergeSort(record, 0, record.size() - 1);
}
};
3. 计算右侧小于当前元素的个数
解题思路:
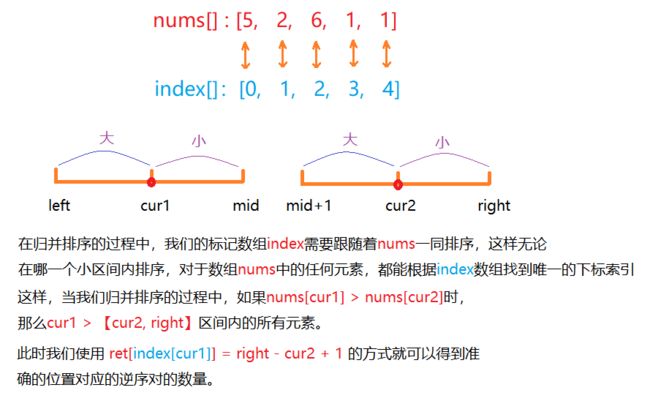
这道题和上一道题目很像,但是不同的是本题需要将数组中的每一个元素的逆序对的个数组成一个新的数组来返回,也就是需要将数组中的每一个元素与其下标建立一一映射关系,但是数组中的元素难免会有重复的,这样的话就不好建立一一对应的映射关系,
当然,思路我们还是上一道题目的思路,不过这里我们增加了数组中的元素和唯一下标的一一对应关系。
代码实现:
class Solution {
public:
vector<int> ret;
vector<int> index;
int tmpN[500010], tmpI[500010];
void MergeSort(vector<int>& nums, int left, int right)
{
if(left >= right) return;
int mid = (left + right) / 2;
MergeSort(nums, left, mid), MergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur1] > nums[cur2])
{
ret[index[cur1]] += right - cur2 + 1;
tmpN[i] = nums[cur1];
tmpI[i++] = index[cur1++];
}
else
{
tmpN[i] = nums[cur2];
tmpI[i++] = index[cur2++];
}
}
while(cur1 <= mid){ tmpN[i] = nums[cur1], tmpI[i++] = index[cur1++]; }
while(cur2 <= right){ tmpN[i] = nums[cur2], tmpI[i++] = index[cur2++]; }
for(int j = left; j <= right; j++)
{
nums[j] = tmpN[j - left];
index[j] = tmpI[j - left];
}
}
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
index.resize(n), ret.resize(n);
for(int i = 0; i < n; i++) index[i] = i;
MergeSort(nums, 0, n - 1);
return ret;
}
};
4. 翻转对
解题思路:
这道题目同样是求逆序对,不过该逆序对需要前一个数大于后一个数的两倍,才能构成满足要求的一个逆序对。
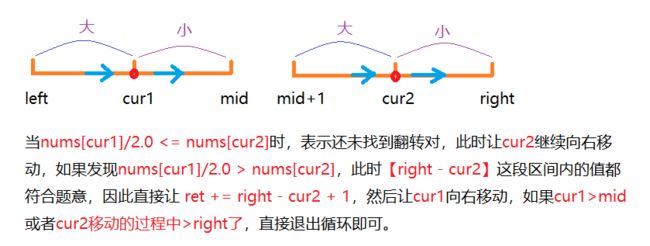
这里我们同样采用归并排序的思想来解决,前面的题目我们都可以使用边排序边求解的方式来进行,但是这道题目前一个数需要大于后一个数的两倍,所以我们不能使用边排序边求解的思路来解决。我们可以先寻找答案然后再排序。下面重点来说一下寻找答案的过程:
这里再已经排好序的两段区间内寻找答案我们可以使用同向双指针的方式来解决。
代码实现:
class Solution {
public:
vector<int> tmp;
int MergeSort(vector<int>& nums, int left, int right)
{
if(left >= right) return 0;
int mid = (left + right) >> 1;
int ret = MergeSort(nums, left, mid) + MergeSort(nums, mid + 1, right);
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur1 <= mid)
{
while(cur2 <= right && nums[cur1]/2.0 <= nums[cur2]) cur2++;
if(cur2 > right) break;
ret += right - cur2 + 1;
cur1++;
}
cur1 = left, cur2 = mid + 1;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur1] > nums[cur2])
tmp[i++] = nums[cur1++];
else
tmp[i++] = nums[cur2++];
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; j++) nums[j] = tmp[j - left];
return ret;
}
int reversePairs(vector<int>& nums) {
tmp.resize(nums.size());
return MergeSort(nums, 0, nums.size() - 1);
}
};