数据结构-----红黑树的插入
目录
前言
红黑树的储存结构
一、节点旋转操作
左旋(Left Rotation)
右旋(Right Rotation)
二、插入节点
1.插入的是空树
2.插入节点的key重新重复
3.插入节点的父节点是黑色
4.插入节点的父节点是红色
4.1父节点是祖父节点的左子节点
4.1.1叔叔节点是红色
4.1.2叔叔节点是黑色
4.1.2-1 插入节点是作左子节点
4.1.2-2插入节点是作右子节点
4.2父节点是祖父节点的右子节点
4.2.1叔叔节点是红色
4.2.2 叔叔节点是黑色
4.2.1-1 插入节点是作左子节点
4.2.1-2 插入节点是作右子节点
三、完整代码展示
前言
上一期我们初步学习了红黑树的基本概念和特性(上一期链接:数据结构-----红黑树简介_Gretel Tade的博客-CSDN博客 如果不了解红黑树相关性质的话建议看看这个),那么从这一期开始,我们就进入到了红黑树的深入学习,首先我通过这一期来详细介绍红黑树的插入操作实现,下面就看看怎么去把数据插入到红黑树吧!
红黑树的储存结构
根据红黑树的要求,我们可以去定义红黑树节点和树的结构体,如下所示:
//宏定义颜色
#define red 0
#define black 1
//数据类型Datatype
typedef char Datatype;
//红黑树节点存储结构
typedef struct node {
Datatype data;
int color;
int key;//排序键值,根据key大小排序
struct node* par;//父节点指针
struct node* left, * right;//左右子节点指针
}Node;
//红黑树的定义rbtree
typedef struct tree {
Node* root;//指向根节点指针
Node* nil;//叶子节点(哨兵)
}rbtree;一、节点旋转操作
在数据结构当中,旋转操作是一种很常见的操作,可能去实现数据结构平衡或者其他相关特性的要求,同样的的AVL树和红黑树里边也是要进行旋转操作的,通过旋转来满足平衡的特性。旋转分两种:左旋(Left Rotation)和右旋(Right Rotation)
左旋(Left Rotation)
左旋是一种将某个节点的右子节点旋转上来的操作。也就是说当前节点的右子节点顶替了自己,然后自己变为右子节点的左子节点,以保持树的平衡。
操作如下:
- 将当前节点的右子节点设为新的父节点。
- 将新的父节点的左子节点设为当前节点的右子节点。
- 如果当前节点有父节点,将新的父节点替代当前节点的位置。
- 将当前节点设为新的父节点的左子节点。
//左旋(以x为旋转点,向左旋转)
void left_rotate(rbtree* T, Node* x) {
Node* y = x->right;//标记到右子节点
x->right = y->left;//y的左子节点代替x的右子节点
if (x->right != T->nil)
x->right->par = x;//如果不为空(nil)其父节点指向x
y->par = x->par;//把y的父节点指向x的父节点,此时x与y没有直接联系了
if (x->par == T->nil) {//判断x的父节点是否为根结点
T->root = y;//如果是的话,y就变为根结点
}
else {
//y顶替x的位置
if (x == x->par->left)
x->par->left = y;//如果x是父节点的左边,那y就代替x成为左子节点
else
x->par->right = y;//如果x是父节点的右边,那y就代替x成为右子节点
}
//y的左子节点指向x,x的父节点指向y
y->left = x;
x->par = y;
}右旋(Right Rotation)
同样的右旋也是将左子节点顶替自己成为父节点, 然后自己成为左子节点的右子节点。
操作如下:
- 将当前节点的左子节点设为新的父节点
- 将新的父节点的右子节点设为当前节点的左子节点
- 如果当前节点有父节点,将新的父节点替代当前节点的位置
- 将当前节点设为新的父节点的右子节点
代码实现:
//右旋(以x为旋转点,向右旋转)
void right_rotate(rbtree* T, Node* x) {
Node* y = x->left;//标记到左子节点y
x->left = y->right;//y的右子节点代替x的左子节点
if (x->left != T->nil)
x->left->par = x;
y->par = x->par;//y的父节点指向x的父节点
if (x->par == T->nil)
T->root = y;//如果x是根结点的话,那么y代替x成为根结点
else {
if (x == x->par->left)
x->par->left = y;
else
x->par->right = y;
}
//y的右子节点指向x,x的父节点为y
y->right = x;
x->par = y;
}二、插入节点
再讲之前,我分享一个网址给大家(链接:Red/Black Tree Visualization),这个是一个红黑树模拟器的网址,你们可以去进行红黑树插入删除遍历等操作,可以自己试试看。如下图所示:
红黑树的插入操作分两步走:
- 找到插入位置
- 进行自平衡调整
注意:插入节点初始为红色
原因分析:因为红黑树中任意一个节点到叶子节点路径所含黑色节点数量相同,也就是说如果我插入的节点为黑色的话,那么就会破坏红黑树的要求,所以插入的节点必须是红色节点,才能保证红黑树的性质。
下面就开始讨论红黑树的几种插入情况:
1.插入的是空树
这是最简单的插入情况,当插入第一个节点的时候,红黑树为空我们只需要让根节点指向这个节点即可。操作如下:
- 根节点指向此节点
- 把根节点染黑
2.插入节点的key重新重复
这种情况的话我们可以根据自己喜好去处理,如果出现了重复的key,那么就把这个key里面的值进行更新;或者我们不进行插入操作,因为key不可以重复,直接退出插入操作。
3.插入节点的父节点是黑色
这很好处理,直接插入就行了,因为父节点为黑色,插入节点为红色,所以不会影响红黑树的平衡性。
- 直接插入即可
4.插入节点的父节点是红色
这种情况是最为复杂的,由于父节点颜色是红色,所以要进行平衡调整,所以要去进一步的讨论才行。那具体根据什么去调整呢?是看叔叔节点的颜色来调整(父节点的兄弟节点),具体分以下几种情况:
大的有两种情况,要看父节点是祖父节点的左边还是右边,下面我就以父节点为左子节点为例子:
下文图标说明:
t 表示插入的节点
P表示父节点
B表示叔叔节点
PP表示祖父节点
4.1父节点是祖父节点的左子节点
4.1.1叔叔节点是红色
如果叔叔节点的颜色是红色的话,这里不需要进行旋转操作,只需要让父节点和叔叔节点颜色变为黑色,祖父节点颜色变为红色即可。流程如下:
- 把P 和B 节点染黑
- 把PP节点染红
4.1.2叔叔节点是黑色
这里的话又要去分两种情况:
- 插入节点是父节点的左子节点
- 插入节点是父节点的右子节点
4.1.2-1 插入节点是作左子节点
如果插入的节点是父节点的左子节点的话,那么要进行以下操作:
- 把P染黑
- 把PP染红
- 对PP进行右旋
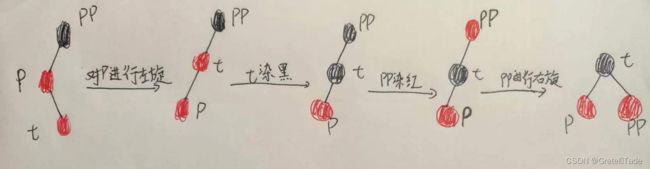
4.1.2-2插入节点是作右子节点
如果插入节点是作为父节点的右子节点的话,要进行以下操作:
- 对P进行左旋
- 把t 染黑
- 把PP染红
- 对PP进行右旋
4.2父节点是祖父节点的右子节点
这里的操作跟4.1基本上是一模一样的,只是对称过去是了,但是我还是想详细列出来吧,下面接着看。
4.2.1叔叔节点是红色
操作步骤如下:
- 把B(叔叔节点)和P(父节点)然黑
- 把PP(祖父节点)染红
4.2.2 叔叔节点是黑色
同样的也是分以下两种情况讨论:
4.2.1-1 插入节点是作左子节点
- 对P 进行右旋
- 将t 染黑
- 将PP 然红
- 对PP 进行左旋
4.2.1-2 插入节点是作右子节点
- 将P 染黑
- 将PP 然红
- 对PP进行左旋
以上这些就是红黑树的插入全部可能了,是不是很多啊,其实还好啦!只要我们把这些情况一个一个分类,然后思路捋一捋很容易弄明白的,后面讲到红黑树的删除还有更多种情况呢!还有就是,这些图片是我自己画的,呃画得不太好,不好意思哈。
三、完整代码展示
#include
#include
#include
#include
//宏定义颜色
#define red 0
#define black 1
//数据类型Datatype
typedef char Datatype;
//红黑树节点存储结构
typedef struct node {
Datatype data;
int color;
int key;
struct node* par;//父节点指针
struct node* left, * right;//左右子节点指针
}Node;
//红黑树的定义rbtree
typedef struct tree {
Node* root;//指向根节点指针
Node* nil;//叶子节点(哨兵)
}rbtree;
//创建初始化红黑树
rbtree* Create_inittree() {
rbtree* T = (rbtree*)malloc(sizeof(rbtree));
assert(T);
T->nil = (Node*)malloc(sizeof(Node));
assert(T->nil);
//T->nil是不储存数据的节点,作为空节点代替NULL,也就是哨兵节点(表示空)
T->nil->color = black;
T->nil->par = NULL;
T->nil->left = T->nil->right = NULL;
T->root = T->nil;
return T;
}
//创建一个节点
Node* Create_node(rbtree*T ,Datatype data, int key) {
Node* new_node = (Node*)malloc(sizeof(Node));
assert(new_node);
new_node->data = data;
new_node->color = red;//初始化颜色红色
//左右父节点为nil哨兵节点
new_node->left=new_node->right = T->nil;
new_node->par = T->nil;
new_node->key = key;
return new_node;
}
//左旋(以x为旋转点,向左旋转)
void left_rotate(rbtree* T, Node* x) {
Node* y = x->right;//标记到右子节点
x->right = y->left;//y的左子节点代替x的右子节点
if (x->right != T->nil)
x->right->par = x;//如果不为空(nil)其父节点指向x
y->par = x->par;//把y的父节点指向x的父节点,此时x与y没有直接联系了
if (x->par == T->nil) {//判断x的父节点是否为根结点
T->root = y;//如果是的话,y就变为根结点
}
else {
//y顶替x的位置
if (x == x->par->left)
x->par->left = y;//如果x是父节点的左边,那y就代替x成为左子节点
else
x->par->right = y;//如果x是父节点的右边,那y就代替x成为右子节点
}
//y的左子节点指向x,x的父节点指向y
y->left = x;
x->par = y;
}
//右旋(以x为旋转点,向右旋转)
void right_rotate(rbtree* T, Node* x) {
Node* y = x->left;//标记到左子节点y
x->left = y->right;//y的右子节点代替x的左子节点
if (x->left != T->nil)
x->left->par = x;
y->par = x->par;//y的父节点指向x的父节点
if (x->par == T->nil)
T->root = y;//如果x是根结点的话,那么y代替x成为根结点
else {
if (x == x->par->left)
x->par->left = y;
else
x->par->right = y;
}
//y的右子节点指向x,x的父节点为y
y->right = x;
x->par = y;
}
//插入后平衡调整
void Insert_adjust(rbtree* T, Node* t) {
//如果父节点的颜色是红色那就进行调整操作了
if (t->par->color == red) {
Node* p = t->par;
Node* pp = p->par;
//01 p节点是pp左子节点
if (p == pp->left) {
Node* uncle = pp->right;
//01-1 叔叔节点颜色是红色
if (uncle->color == red) {
p->color = black;
uncle->color = black;
pp->color = red;
t = pp;
}
//01-2 叔叔节点颜色是黑色
else {
//01-2-1 插入节点t是p的左子节点
if (t == p->left) {
p->color = black;
pp->color = red;
right_rotate(T, pp);
t = p;
}
//01-2-2 插入节点t是p的右子节点
else if(t==p->right){
left_rotate(T, p);
t->color = black;
pp->color = red;
right_rotate(T, pp);
}
}
}
//02 p节点是pp的右子节点
else {
Node* uncle = pp->left;
//02-1 叔叔节点颜色是红色
if (uncle->color == red) {
pp->color = red;
p->color = black;
uncle->color = black;
t = pp;
}
//02-2 叔叔节点颜色是黑色
else {
//02-2-1 插入节点t是p的右子节点
if (t == p->right) {
p->color = black;
pp->color = red;
left_rotate(T,pp);
t = p;
}
//02-2-2 插入节点t是p的左子节点
else {
right_rotate(T, p);
t->color = black;
pp->color = red;
left_rotate(T, pp);
}
}
}
}
//根节点标记黑色
T->root->color = black;
}
//插入节点
void Insert_node(rbtree* T, Datatype data,int key) {
assert(T);
Node* t = Create_node(T ,data, key);
Node* root = T->root;//快指针
Node* cur=T->nil;//慢指针
//1.如果根节点为空
if (T->root==T->nil) {
T->root = t;//根结点指向新创建的节点
}
else {
while (root != T->nil) {
cur = root;//cur标记为root的上一个节点(父节点)
if (t->key > root->key)
root = root->right;
else if (t->key < root->key)
root = root->left;
//如果出现插入重复的key值,就退出,不进行插入操作
else {
printf("Don't insert the same key!\n");
free(t);
t = NULL;
return;
}
}
}
//判断插入的位置
if (key < cur->key)
cur->left = t;//小的话就插入左边
else
cur->right = t;//大的话就插入右边
t->par = cur;//新插入的父节点指针指向cur
Insert_adjust(T, t);//平衡调整
} 单单值考虑插入操作就有两百多行代码,后面还有删除操作,查找操作,总共的话大概400行代码,这里就先发今天所讲的插入操作内容的代码,注释很详细,慢慢看哈,我相信你一点看得懂的!
以上就是本期的全部内容了,我们下一期讲红黑树的删除操作,下次见!
分享一张壁纸: